Исследование операций. Решение для минимума Поскольку функция цели F(x) параллельна de то на прямой de функция F(x) будет принимает одно и тоже минимальное значение. Для определения координат точки e решим систему уравнений
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
|
Задача 1  Найдем вначале область допустимых решений (ОДР) x1-3x2=-8, Эта прямая проходит через точки: (-8,0), ( 0, 8/3). 3x1-x2=8, Эта прямая проходит через точки: (8/3,0), ( 0, -8). x1-x2=2, Эта прямая проходит через точки: (2,0), ( 0, -2). x1+x2=2, Эта прямая проходит через точки: (2,0), ( 0, 2). x1-x2=-2, Эта прямая проходит через точки: (-2,0), ( 0, 2). x1 ≥ 0, x2 ≥ 0, Тривиальным неравенствам x1 0, x2 0 соответствует первая четверть координатной плоскости. Пересечение всех указанных полуплоскостей определяет ОДР данной задачи. 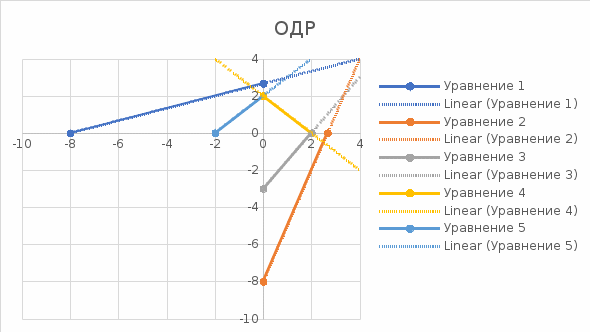 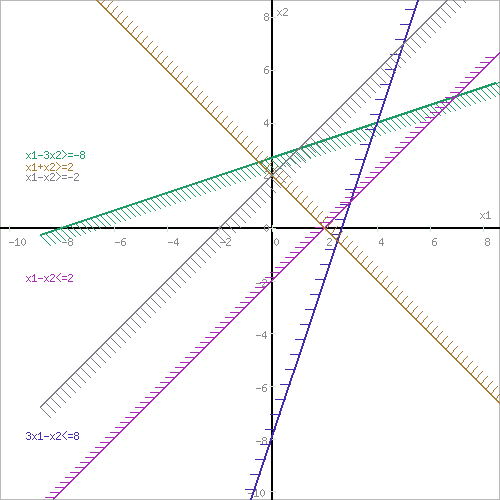 Выделив область решения каждого неравенства системы ограничений, получим многоугольник допустимых решений нашей задачи. 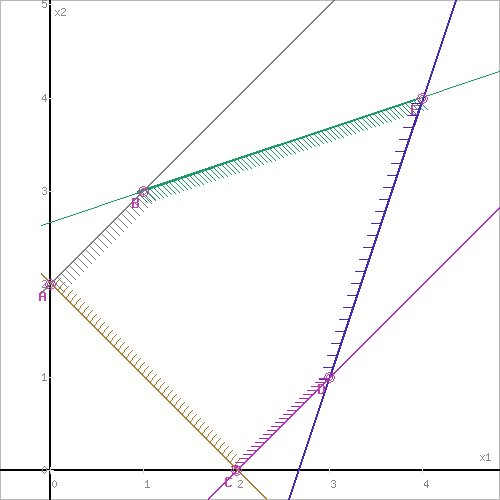 Получили многоугольник ABCDE Построим основную прямую F = -9x1+3x2+18 = 0, проходящую через начало координат O(0,0) перпендикулярно вектору c(-9;3). 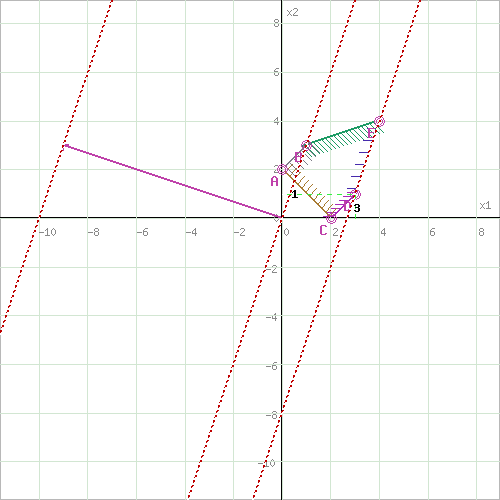 Перемещая прямую F в направлении вектора c(-9;3), находим минимальную точку D, в которой пересекаются прямые 2 и L: 3x1-x2=8 x1-x2=2 Решим систему уравнений и получим: x1 = 3, x2 = 1 Откуда найдем минимальное значение целевой функции: F(x) = -9∙3 + 3∙1 + 18 = -6 Решение для минимума: 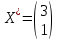 Поскольку функция цели F(x) параллельна DE то на прямой DE функция F(x) будет принимает одно и тоже минимальное значение. Для определения координат точки E решим систему уравнений: x1-3x2=-8 3x1-x2=8 Получим: x1 = 4, x2 = 4 F(x) = -9∙4 + 3∙4 + 18 = -6 тоже самое минимальное значение. Решение для минимума: 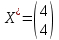 Перемещая прямую F в направлении вектора c(-9;3), находим максимальную точку A, в которой пересекаются прямые 5 и 6: x1-x2=-2 x1=0 Решив систему уравнений, получим: x1 = 0, x2 = 2 Откуда найдем максимальное значение целевой функции: F(x) = -9∙0 + 3∙2 + 18 = 24 Решение для максимума: 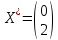 Ответ: Минимальное значение -6 достигается при x1 = 3, x2 = 1. Максимальное значение 24 достигается при x1 = 0, x2 = 2. Задача 2 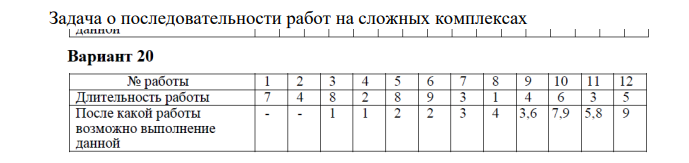 Строим граф: 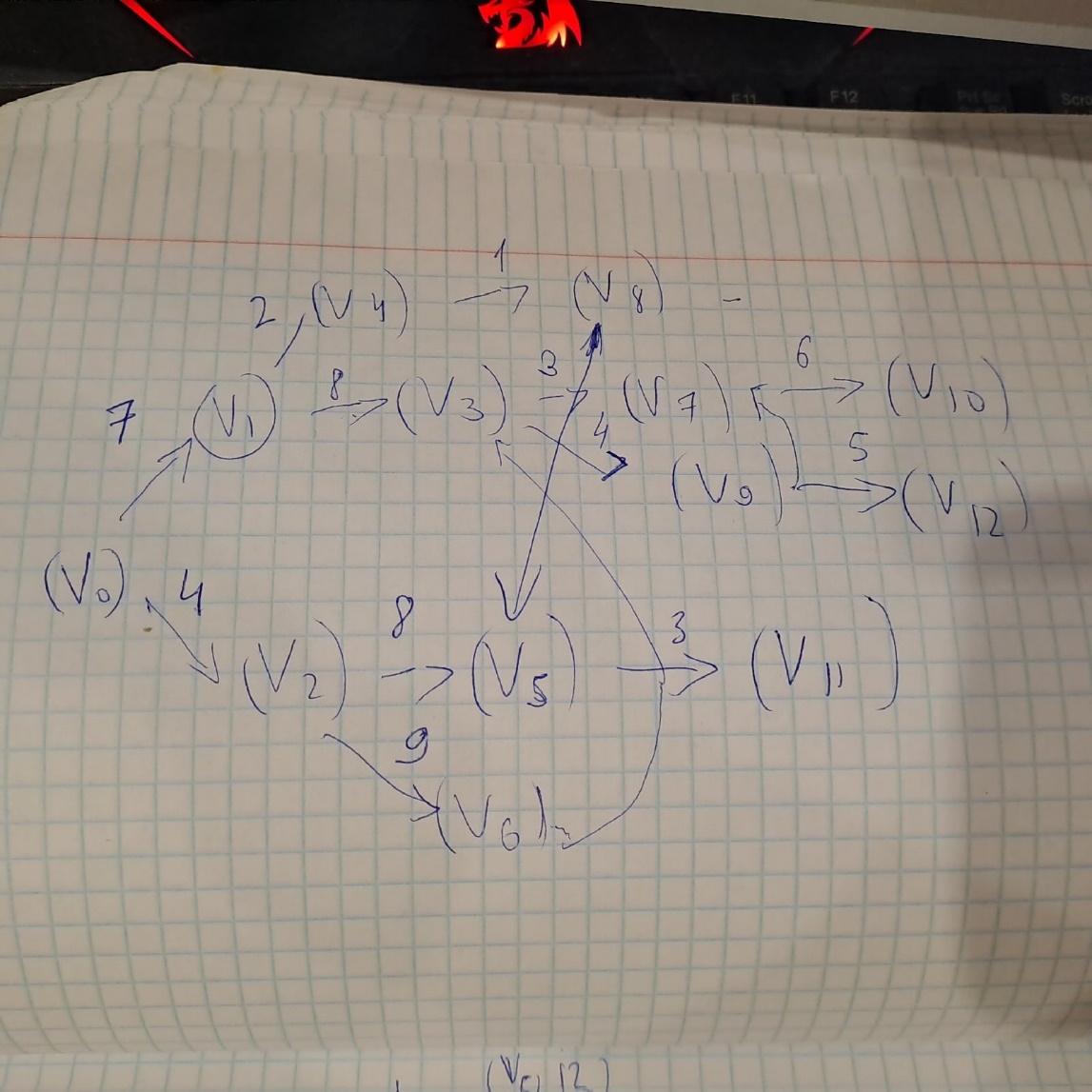 Каждой вершине присвоим двойную метку Vi ,li , где Vi – вершина из которой путь приходит, li – длина пути до этой вершины. 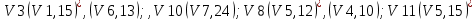 Отметим красным цветом наилучший путь и запишем его. 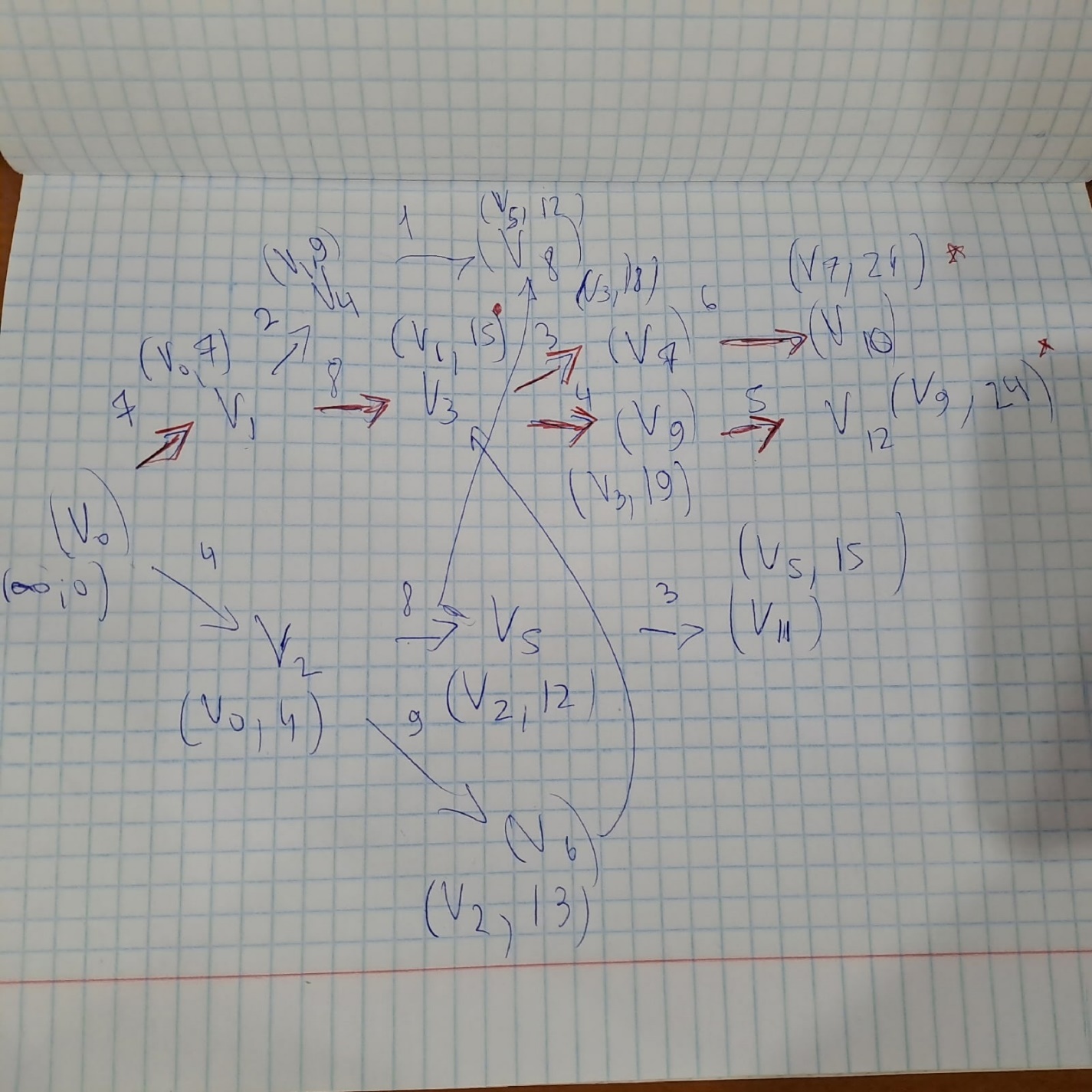 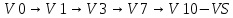 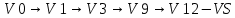 Lmax = 24 Ответ: Lmax = 24, 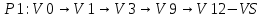 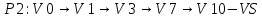 Задача 3 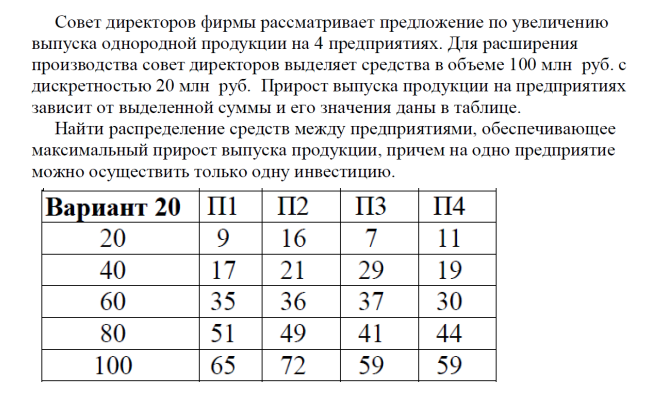 Исходные данные.
Динамическое программирование. Условная оптимизация. 1-ый шаг. k = 4.
2-ый шаг. k = 3.
3-ый шаг. k = 2.
4-ый шаг. k = 1.
Столбцы 1, 2 и 3 для всех 4 таблиц одинаковы. Столбец 4 заполняется на основе данных о функциях дохода, значения в столбце 5 беререм из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5. В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7. Безусловная оптимизация. Из таблицы 4-го шага имеем F*1(e0 = 100) = 73. То есть максимальный доход при количестве средств e0 = 100 равен 73. 1-му предприятию следует выделить u*1(e0 = 100) = 0 Остаток средств составит: e1 = e0 - u1 e1 = 100 - 0 = 100 Из таблицы 3-го шага имеем F*2(e1 = 80) = 58. То есть максимальный доход при количестве средств e1 = 100 равен 58 2-му предприятию следует выделить u*2(e1 = 80) = 40 При этом остаток средств составит: e2 = e1 - u2 e2 = 80 -40 = 40 Из таблицы 2-го шага имеем F*3(e2 = 60) = 40. То есть максимальный доход при количестве средств e2 = 60 равен 40 Из этой же таблицы получаем, что 3-му предприятию следует выделить u*3(e2 = 60) = 40 При этом остаток средств составит: e3 = e2 - u3 e3 = 60 - 40 = 20 Последнему предприятию достается 100-20-40=40 Итак, инвестиции в размере 100 необходимо распределить следующим образом: 1-му предприятию выделить 40 2-му предприятию выделить 20 3-му предприятию выделить 40 4-му предприятию выделить 0 Что обеспечит максимальный доход, равный 73 |
