Задача 1 2 задача 2 7 задача 3 10 Ответы на контрольные вопросы 20 задача 1
 Скачать 215.16 Kb. Скачать 215.16 Kb.
|
СодержаниеЗАДАЧА 1 2 ЗАДАЧА 2 7 ЗАДАЧА 3 10 Ответы на контрольные вопросы: 20 ЗАДАЧА 1
Целевая функция: Z=2x1+9x2 – max Ограничения: x1-3x2 >= -12 2x1 +x2<= 20 5x1+6x2<=57 x1>=0 x2>=0 Решаем графически: Запишем уравнения граничных прямых и построим их на плоскости x10x2. x1-3x2=-12, (1) 2x1+x2=20, (2) 5x1+6x2=57, (3) x1 ≥ 0, (4) x2 ≥ 0, (5) 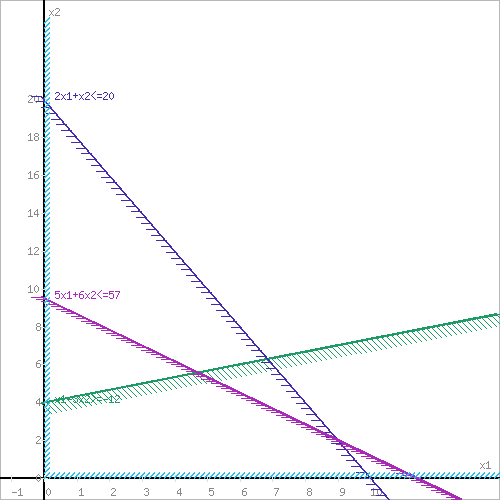 Выделив область решения каждого неравенства системы ограничений, получим многоугольник допустимых решений ЗЛП. 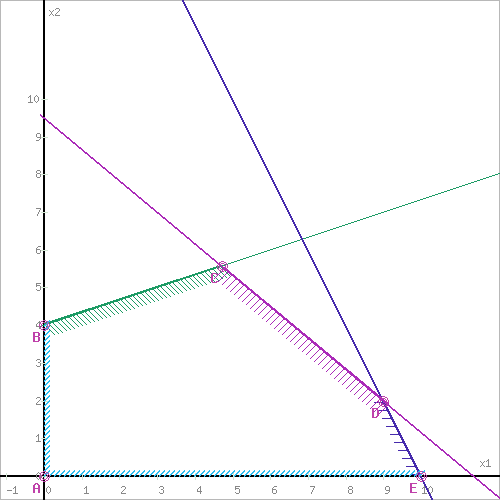 Построим основную прямую L = 0, то есть Z = 2x1+9x2 = 0, проходящую через начало координат O(0,0) перпендикулярно вектору c(2;9). 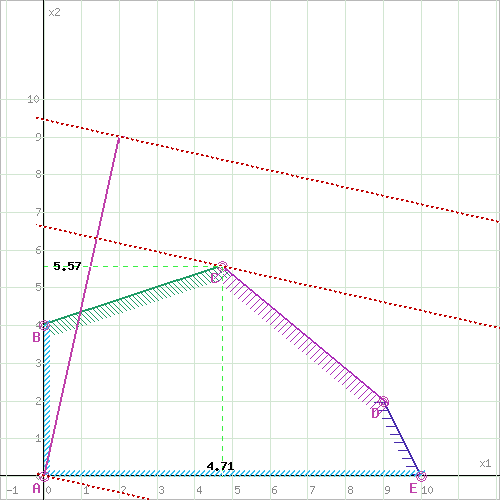 На рисунке видно, что областью допустимых решений является многоугольник ABCDE. Перемещая прямую L = 0 в направлении вектора c(2;9), находим максимальную точку C, в которой пересекаются прямые L1 и L3: x1-3x2=-12 5x1+6x2=57 Решив систему уравнений, получим: x1 = 4.7143, x2 = 5.5714 Откуда найдем максимальное значение целевой функции: Z(x1,x2) = 2*4.7143 + 9*5.5714 = 59.5714 Проверим правильность решения через математические пакеты MathCad и Excel. Ниже представлен листинг поиска решения задачи оптимизации в пакете MathCad. 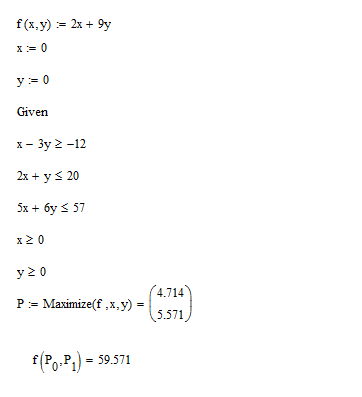 Как видно из листинга, решение совпадает с графическим методом Решим задачу в пакете Excel с помощью функции «Поиск Решения». 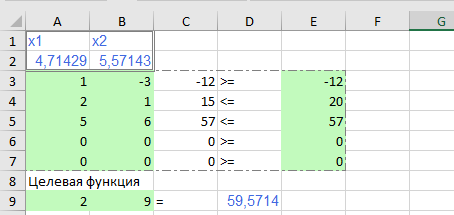 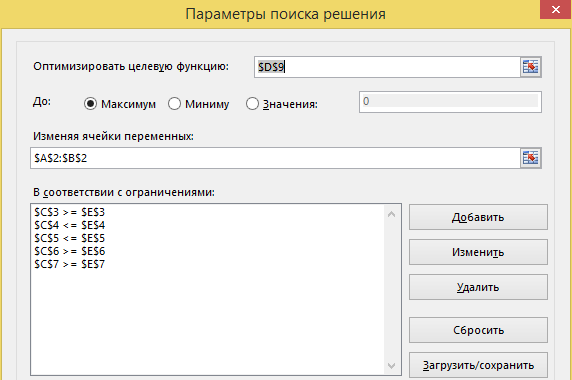 Как видно из полученных данных, решение так же полностью совпадает с графическим методом. Все три метода совпали. ЗАДАЧА 2Со станции формирования ежедневно отправляются пассажирские и скорые поезда, составленные из плацкартных, купейных и мягких вагонов. Число мест в плацкартном вагоне – 54, в купейном – 36, в мягком – 18. В таблице указаны состав поезда каждого типа и количество имеющихся в парке вагонов различного типа. Определить число скорых и пассажирских поездов, которые необходимо формировать ежедневно, чтобы число перевозимых пассажиров было максимальным.
Обозначим x1 – число скорых поездов, x2 – число пассажирских поездов. Число мест в скором поезде: 1*54+7*36+2*18=342. Число мест в пассажирском поезде: 5*54+6*36+2*18=522. Запишем математическую модель задачи: F(x)=342x1+522x2 --- max. Определим ограничения: Количество поездов не может быть отрицательным, соответственно: 1) x1>=0; 2) x2>=0. Ограничение по парку плацкартных вагонов: 3) x1+5x2<=50. Ограничение по парку купейных вагонов: 4) 7x1+6x2<=91. Ограничение по парку мягких вагонов: 5) 2x1+2x2<=28. Получилось 5 ограничений. Решим данную задачу симплекс методом в математическом пакете Excel и MathCad. Воспользуемся пакетом Excel «Поиск решения». 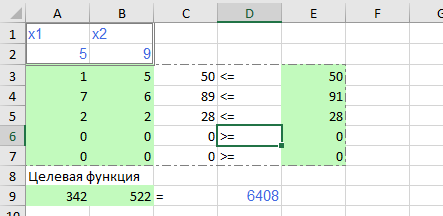 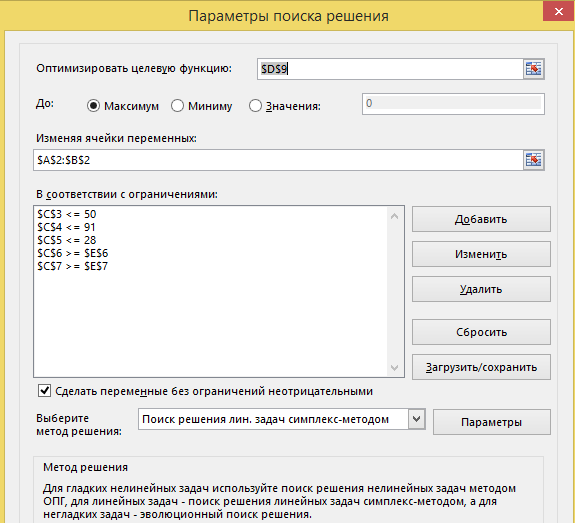 Делаем вывод, что целевая функция равна 6408. Значит, максимально число пассажиров, равное 6408, достигается при 342 скорых и 522 пассажирских поездах. Проверим данное решение в пакете MathCad, листинг представлен ниже. 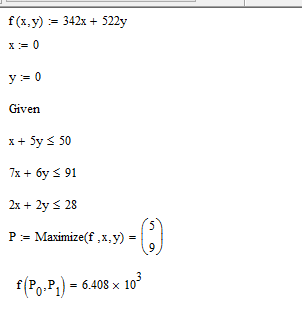 Результат совпал, что говорит о верности решения. |
