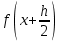РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2. Решение Для нахождения первообразной воспользуемся таблицей интегралов Решение Для нахождения данного интеграла сделаем замену

• Название: Решение Для нахождения первообразной воспользуемся таблицей интегралов Решение Для нахождения данного интеграла сделаем замену
• Дата: 19.04.2023
• Размер: 253.14 Kb.
• Имя файла: РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2.docx
• Тип: Документы; #1073951

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уральский государственный университет путей сообщения»

(ФГБОУ ВО УрГУПС)

Кафедра «Естественнонаучные дисциплины»

Дисциплина «Математика»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №2

«ИНТЕГРАЛЬНОЕ ИСЧЕСЛЕНИЯ. ФНП»

 

Вариант 4

Проверил:   Выполнил студент:

доцент, к.ф.-м.н.    группы СОт-112(з)

Мезенцев А.В Крипак М.Е.

Екатеринбург

2023

задачи

1. 
   Найти неопределенный интеграл:
   

Решение:

Для нахождения первообразной воспользуемся таблицей интегралов:




Решение:

Для нахождения данного интеграла сделаем замену: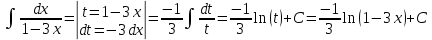




Решение:

Для нахождения данного интеграла также сделаем замену: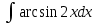





Решение:

Для вычисления данного интеграла воспользуемся методом интегрирования по частям :



Внесём под дифференциал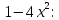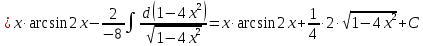

2. 
   Вычислить несобственный интеграл или доказать его расходимость.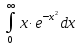
   

Решение:

Для вычисления данного интеграла, внесём под дифференциал и воспользуемся формулой Ньютона-Лейбница:

3. 
   В декартовой системе координат построить плоскую фигуру, ограниченную линиями. Найти площадь фигуры.
   

Решение:

Построим фигуру на плоскости, площадь которой нам нужно найти:



Получили фигуру, ограниченную двумя параболами,вычислим её площадь по формуле: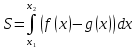



Где функция «выше» (парабола ), а функция «ниже» (парабола ). А и границы интегрирования по абсцисс, найдем их:







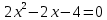Тогда:

4. 
   Интеграл вычислить точно по формуле Ньютона-Лейбница и приближенно по формуле прямоугольников. Отрезок интегрирования разбить на 10 частей. Все вычисления проводить, сохраняя четыре знака после запятой. Приближенное значение интеграла округлить до третьего десятичного знака. Найти абсолютную и относительную погрешность результата вычислений.
   

Решение:

Вычислим интеграл по формуле Ньютона Лейбница:



Теперь вычислим этот же интеграл с помощью формулы прямоугольников приближенно:

Начнём с вычисления шага разбиения, т. к. по заданию количество отрезков разбиения равно 10 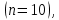то шаг разбиения вычисляется как:



Где верхняя граница интегрирования, а нижняя:



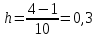по формуле средних прямоугольников: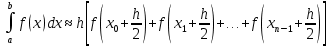



Тогда, нам необходимо найти значения функции в серединах промежуточных отрезков, для этого проще занести все вычисления в таблицу, при этом все вычисления будем округлять до 4 знаков после запятой:

	0	1	2	3	4	5	6	7	8	9	10
	1	1,3	1,6	1,9	2,2	2,5	2,8	3,1	3,4	3,7	4
	1,15	1,45	1,75	2,05	2,35	2,65	2,95	3,25	3,55	3,85	-
	1,7505	0,7876	0,4484	0,2932	0,2090	0,1577	0,1239	0,1002	0,0829	0,0698	-

Теперь подставим найденные значения в формулу и вычислим интеграл:



При этом абсолютная погрешность измерений:



А относительная: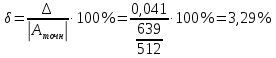

5. 
   Найти и показать на плоскости 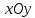область определения функции:
   

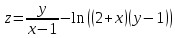Решение:

Чтобы найти область определения, рассмотрим все точки разрыва и области определения элементарных функций:



По свойству логарифма, логарифмическое выражение должно быть 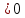т. е.:



Получается, что область определения функции находится в 2 и 4 четверти при смещении центра координат в точку 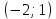, изобразим это на чертеже:

6. 
   Найти частные производные функции двух переменных:
   

Решение:

Для вычисления частных производных воспользуемся таблицей производных, правилом дифференцирования сложных функций и произведения: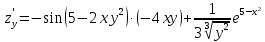

7. 
   Исследовать функцию двух переменных на экстремум:
   

Решение:

Отыщем стационарные точки, найдя частные производные по :





Решим следующую систему:



Нашли две точки стационарные точки

Воспользуемся достаточным условием функции двух переменных и рассмотрим первую точку, для этого введем обозначение: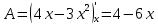









Тогда для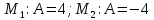

Рассмотрим следующее неравенство: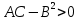





Неравенство выполняется, значит экстремум есть, а т.к. 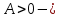то в этой точке минимум. Аналогично распишем точку



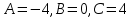Неравенство:



Отсюда следует, что в точке экстремума нет.

8. 
   Найти градиент функции в точке и производную в направлении, идущем от этой точки к точке
   

Решение:

Вычислим градиент по следующей формуле:



Для этого найдем частные производные: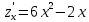





Тогда величина градиента: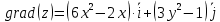



Теперь найдем градиент в точке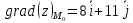



Направление градиента найдем с помощью направляющих косинусов, направляющий вектор: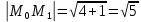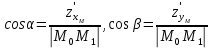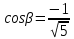









Тогда: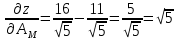