Прикладная механика задача №1. Задача №2 прикладная механика. Решение. Для определения траектории точки исключим из заданных уравнений движения время t. Используем формулу. В данном случае
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Задача 2 Точка А движется в плоскости ху. Закон движения точки задан уравнениями 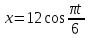 и и 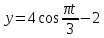 . При этом координаты х и у выражены в сантиметрах, а время t – в секундах. Найти уравнение траектории точки, изобразить траекторию на рисунке; для момента времени t = 1 с определить и указать на рисунке скорость и ускорение точки, а также её касательное и нормальное ускорение и радиус кривизны траектории. . При этом координаты х и у выражены в сантиметрах, а время t – в секундах. Найти уравнение траектории точки, изобразить траекторию на рисунке; для момента времени t = 1 с определить и указать на рисунке скорость и ускорение точки, а также её касательное и нормальное ускорение и радиус кривизны траектории.Решение. Для определения траектории точки исключим из заданных уравнений движения время t. Используем формулу 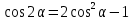 . В данном случае . В данном случае 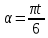 . .Из уравнения 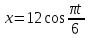 получаем получаем 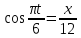 Из уравнения Из уравнения 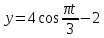 получаем получаем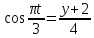 , , а так как 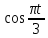 =2 =2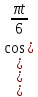 , получим , получим 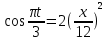 – 1 или – 1 или 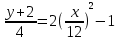 , умножим обе части уравнения на 4 получим , умножим обе части уравнения на 4 получиму+2 = 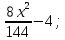 выразим из уравнения у, получим у = выразим из уравнения у, получим у =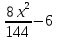 или илиу = 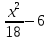 это уравнение параболы, ветви которой направлены вверх, а вершина смещена на -6см по оси у. Изобразим найденную траекторию. Для более точного изображения найденной траектории по заданным уравнениям движения определим положение точки в различные моменты времени. это уравнение параболы, ветви которой направлены вверх, а вершина смещена на -6см по оси у. Изобразим найденную траекторию. Для более точного изображения найденной траектории по заданным уравнениям движения определим положение точки в различные моменты времени. 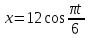 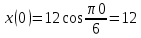 ·1=12 ·1=12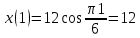 ·0,866=10,39 ·0,866=10,39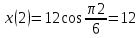 ·0,5= 6 ·0,5= 6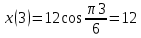 ·0 = 0 ·0 = 0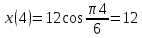 ·(-0,5_) = - 6 ·(-0,5_) = - 6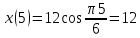 ·(-0,866) = -10,39 ·(-0,866) = -10,39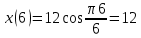 ·(-1)= -12 ·(-1)= -12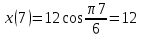 ·(-0,866) = -10,39 ·(-0,866) = -10,39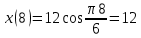 ·(-0,5)= - 6 ·(-0,5)= - 6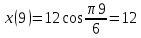 ·0 = 0 ·0 = 0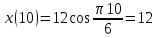 ·0,5 = 6 ·0,5 = 6 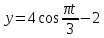 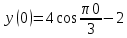 = 4·1 – 2 = 2 = 4·1 – 2 = 2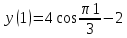 = 4·0,5 – 2 = 0 = 4·0,5 – 2 = 0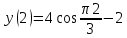 = 4·(-0,5) – 2 = - 4 = 4·(-0,5) – 2 = - 4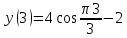 = 4·(-1 ) – 2 = - 6 = 4·(-1 ) – 2 = - 6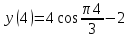 = 4·(-0,5) – 2 = - 4 = 4·(-0,5) – 2 = - 4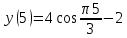 = 4·0,5 – 2 = 0 = 4·0,5 – 2 = 0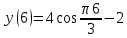 = 4·1 – 2 = 2 = 4·1 – 2 = 2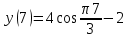 = 4·0,5 – 2 = 0 = 4·0,5 – 2 = 0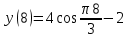 = 4·(-0,5) – 2 = -4 = 4·(-0,5) – 2 = -4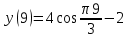 = 4·(-1) – 2 = - 6 = 4·(-1) – 2 = - 6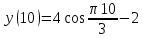 = 4·(-0,5) – 2 = -4 = 4·(-0,5) – 2 = -4Заполним таблицу координат точки в различные моменты времени
( 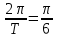 , Т=12 Точка движется по параболе с периодом 12 секунд, через 6 секунд она начинает обратное движение.) , Т=12 Точка движется по параболе с периодом 12 секунд, через 6 секунд она начинает обратное движение.)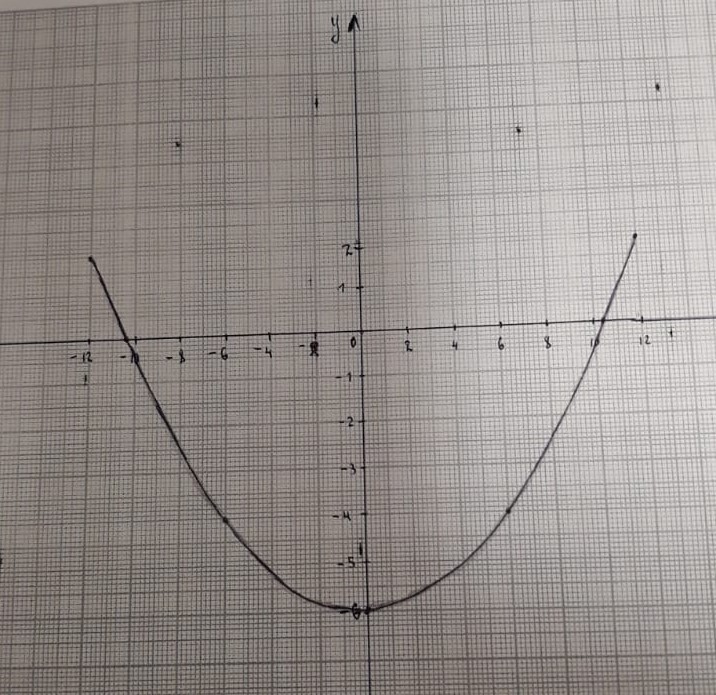 Рисунок 3. Траектория движения точки Скорость точки найдем через её проекции на координатные оси: 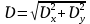 где Ʋх - проекция вектора скорости на ось х, а Ʋу - проекция вектора скорости на ось у. Проекция вектора скорости на ось х равна первой производной по времени от уравнения движения для координаты х: Ʋх = 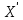 Ʋх = 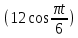 ’ = -12 ’ = -12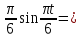 - -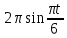 Найдем значение Ʋх при t=1; Ʋх= - 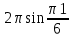 = -2 = -2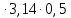 = -3,14 = -3,14Проекция вектора скорости на ось у равна первой производной по времени от уравнения движения для координаты y: Ʋy = y’ Ʋу = 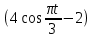 ’ = - 4 ’ = - 4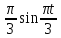 Найдем значение Ʋу при t=1; Ʋу = -4 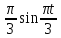 = - = -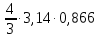 = -3,6257 = -3,6257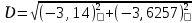 = =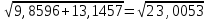 = 4,7964 = 4,7964 Ускорение точки найдем через её проекции на координатные оси: 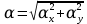 где ɑх - проекция вектора скорости на ось х, а ɑу - проекция вектора скорости на ось у. ɑ Проекция вектора ускорения на ось х равна первой производной по времени от проекции вектора скорости на ось х: ɑх = Ʋх’ ɑх = 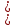 - -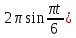 ’ = -2 ’ = -2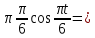 - -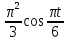 Найдем значение ɑх при t=1; ɑ(1)х = - 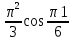 = - = -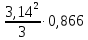 = -2, 8461 см/с2 = -2, 8461 см/с2Проекция вектора ускорения на ось у равна первой производной по времени от проекции вектора скорости на ось у: ɑу = Ʋу’ ɑу = 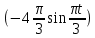 ’ = - 4 ’ = - 4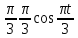 = - 4 = - 4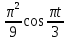 Найдем значение ɑу при t=1; ɑу = -4 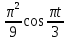 = - = -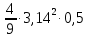 = -2,1910 см/с2 = -2,1910 см/с2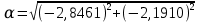 = =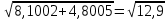 = 3,5917см/с2 = 3,5917см/с2Касательное ускорение определяем по формуле: 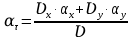 . . Для момента времени t=1 получаем 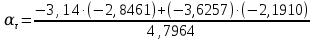 = =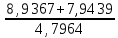 = 3,5194см/с2. = 3,5194см/с2. Нормальное ускорение определяем по формуле: 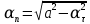 . Для момента времени t=1 получаем . Для момента времени t=1 получаем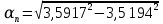 = =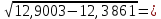 = 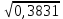 = 0,6189 cм/с2. = 0,6189 cм/с2.По полученным данным изобразим αх и αу - составляющие вектора ускорения и α - вектор полного ускорения точки А. Вектор нормального ускорения 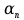 всегда направлен перпендикулярно траектории в сторону её вогнутости (к центру окружности проходящей через точку А). Вектор касательного ускорения всегда направлен перпендикулярно траектории в сторону её вогнутости (к центру окружности проходящей через точку А). Вектор касательного ускорения  всегда располагается по касательной к траектории в ту сторону, чтобы выполнялось уравнение ᾱ = ᾱn + ᾱτ В нашем случае направление вектора ᾱ τ совпадает с направлением вектора Ʋ, следовательно, точка А движется ускоренно. всегда располагается по касательной к траектории в ту сторону, чтобы выполнялось уравнение ᾱ = ᾱn + ᾱτ В нашем случае направление вектора ᾱ τ совпадает с направлением вектора Ʋ, следовательно, точка А движется ускоренно.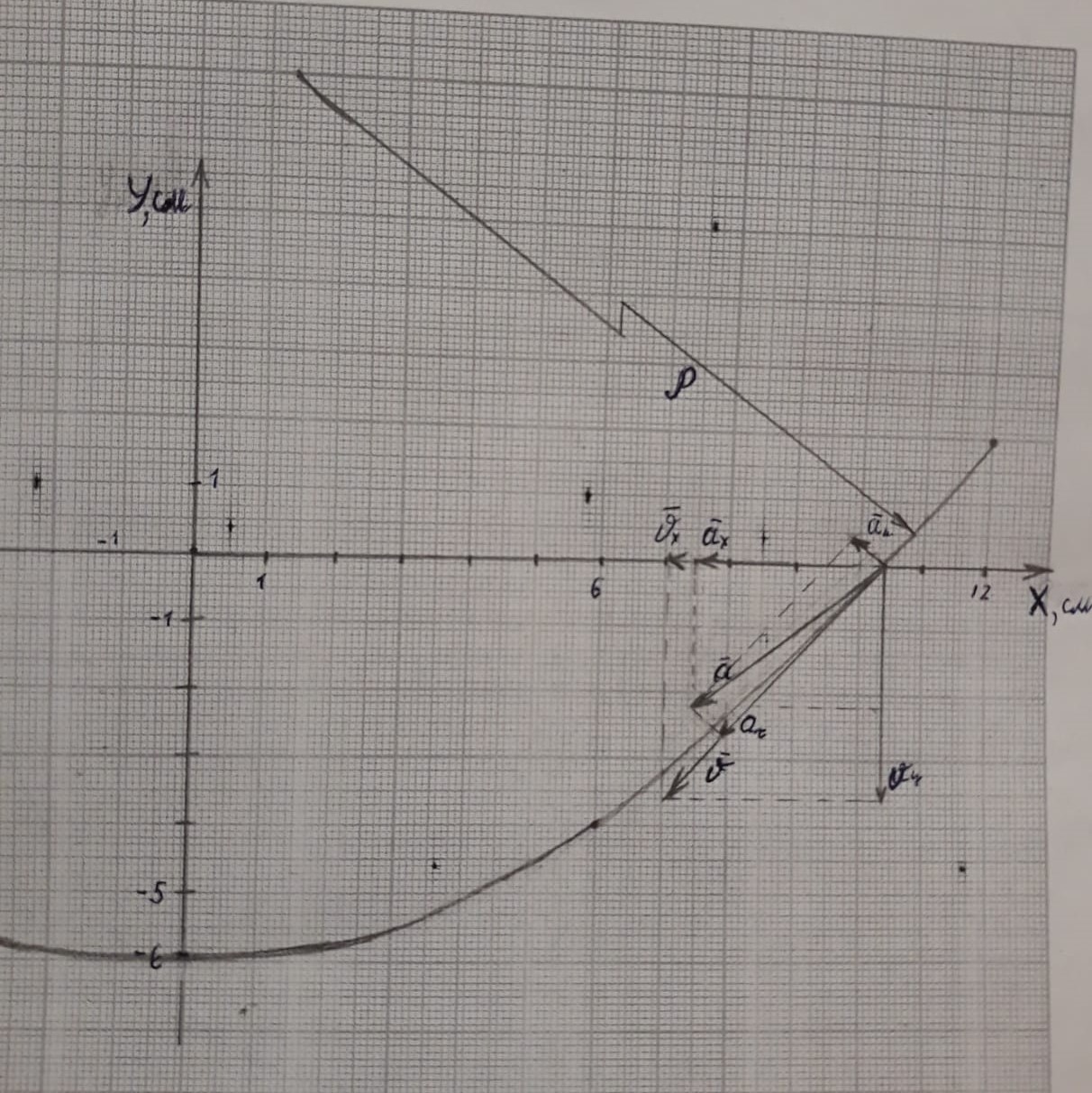 Рисунок 4. Траектория движения и кинематические параметры точки Радиус кривизны траектории определяем по формуле 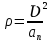 . . Для момента времени t=1с получаем: 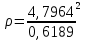 = 37,17см. = 37,17см. Изображаем радиус кривизны траектории как радиус окружности, которая проходит через точку А, а центр окружности находится на нормали к траектории. (Радиус окружности проведенный к точке А и вектор нормального ускорения в точке А совпадают) Ответ: Ʋ = 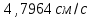 ; α = 3,5917см/с2; ; α = 3,5917см/с2; 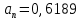 см/с2; см/с2; 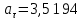 см/с2; см/с2; 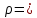 37,17см. 37,17см. |
