Задача К1. ЭПб-20-1 Фатеев С.А. Задание К1 Вариант 96. ЭПб201 Фатеев С. А. Задание К1
 Скачать 275.23 Kb. Скачать 275.23 Kb.
|
|
ЭПб-20-1 Фатеев С.А. Задание К1 Вариант 96 По заданным уравнениям движения точки 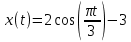 , , 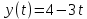 , где координаты х и у измеряются в сантиметрах, а время t в секундах, найти уравнение траектории точки, ее скорость, нормальное, касательное и полное ускорения, а также радиус кривизны траектории для момента времени t1 = 1с. На рисунке изобразить траекторию и для заданного момента времени t1 = 1с в выбранном масштабе построить векторы скорости и ускорения точки. , где координаты х и у измеряются в сантиметрах, а время t в секундах, найти уравнение траектории точки, ее скорость, нормальное, касательное и полное ускорения, а также радиус кривизны траектории для момента времени t1 = 1с. На рисунке изобразить траекторию и для заданного момента времени t1 = 1с в выбранном масштабе построить векторы скорости и ускорения точки.Нахождение траектории движения точки М. Для нахождения уравнения траектории, следует из уравнений исключить время. Выразим t из уравнения 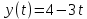 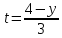 (1) (1)Подставляем в уравнение 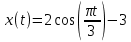 уравнение (1). В результате получим уравнение траектории движения точки уравнение (1). В результате получим уравнение траектории движения точки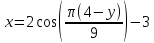 (2) (2)Уравнение (2) представляет собой косинусоиду. Построение траектории. Изобразим на рисунке траекторию точки и путем подстановки в уравнение движения точки заданного момента времени t1=1 c определим положение точки на траектории. Для этого выберем масштаб, например Xt=-2 см, yt=1 см 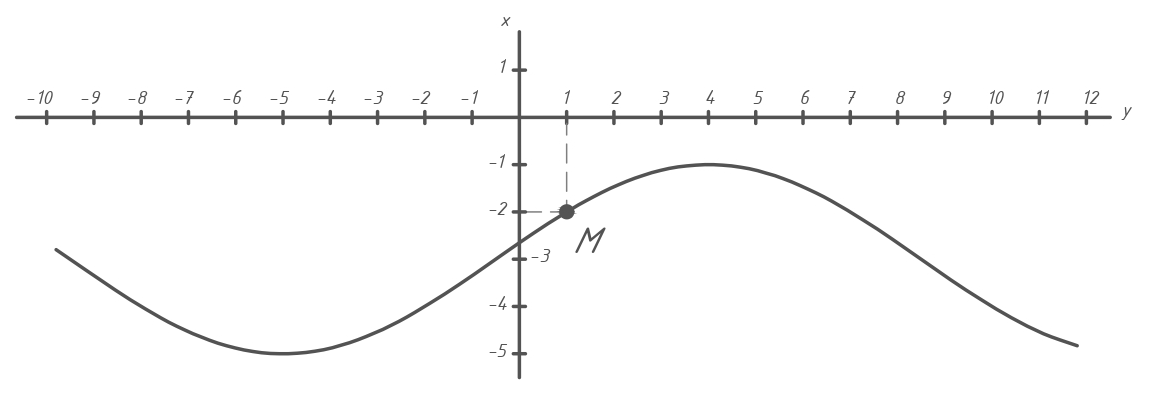 Рис. 1 Нахождение величины скорости точки Для вычисления скорости точки, движение которой задано координатным способом, применяется формула 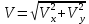 , (3) , (3)где 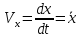 , , 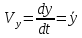 – проекции вектора скорости точки на оси координат. – проекции вектора скорости точки на оси координат.Вычисляя производные от соответствующих уравнений движения точки по времени, получаем следующие формулы 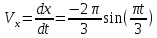 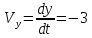 Вычисляем величины проекций вектора скорости на оси координат в момент времени t=1 с 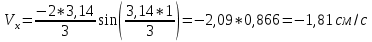 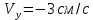 А затем, подставляя величины 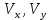 в уравнение (3), определим величину скорости точки в уравнение (3), определим величину скорости точки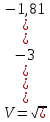 Для построения вектора скорости точки, воспользуемся формулой 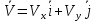 Выбираем масштаб и на рисунке из точки М в выбранном масштабе откладываем составляющие вектора скорости 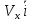 , , 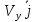 , а затем проводим вектор , а затем проводим вектор 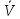 (рис. 2) (рис. 2)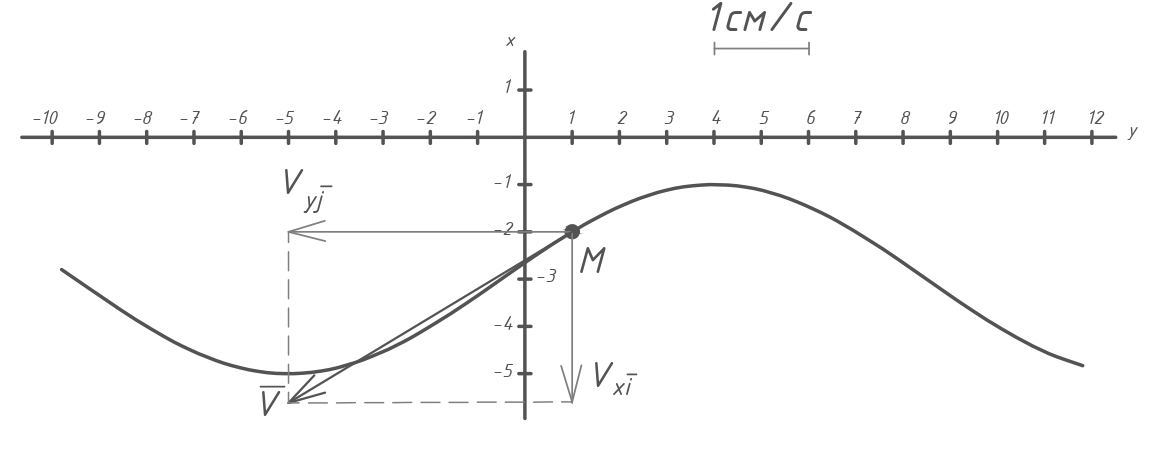 Рис. 2 Нахождение величины вектора ускорения точки. Величина ускорения точки при задании ее движения координатным способом вычисляется по формуле 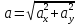 , ,где 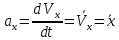 , , 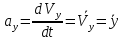 – проекции вектора ускорения на оси координат, которые определяются выражениями – проекции вектора ускорения на оси координат, которые определяются выражениями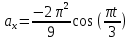 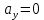 При t=1 c имеем: 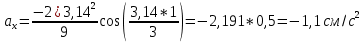 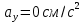 По найденным проекциям вычисляем полное ускорение точки 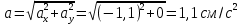 Применив формулу 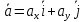 , построим на рис. 3 вектор полного ускорения точки , построим на рис. 3 вектор полного ускорения точки 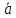 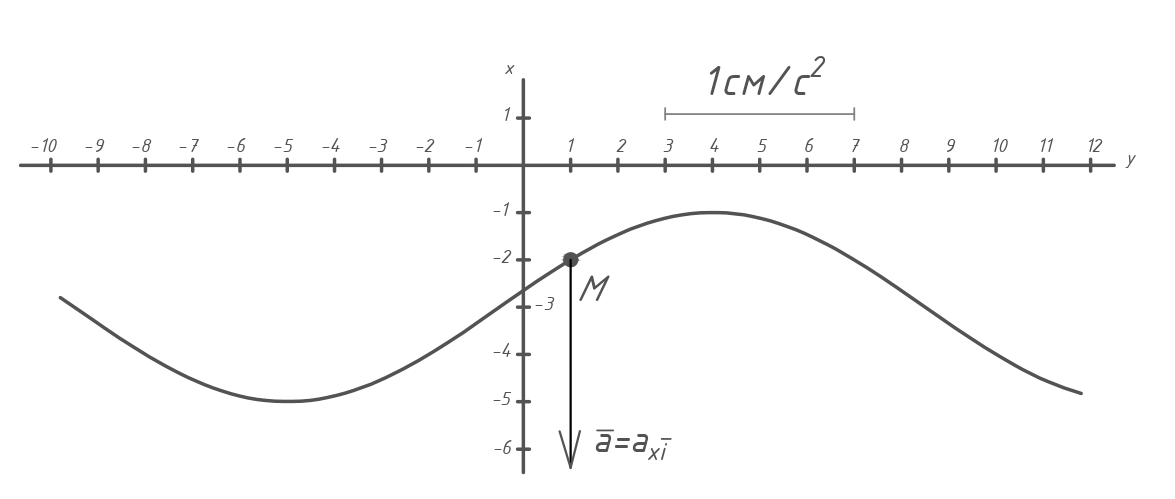 Рис. 3 На рис. 4 для момента времени t1=1 c выполнены построения векторов скорости и ускорения точки. 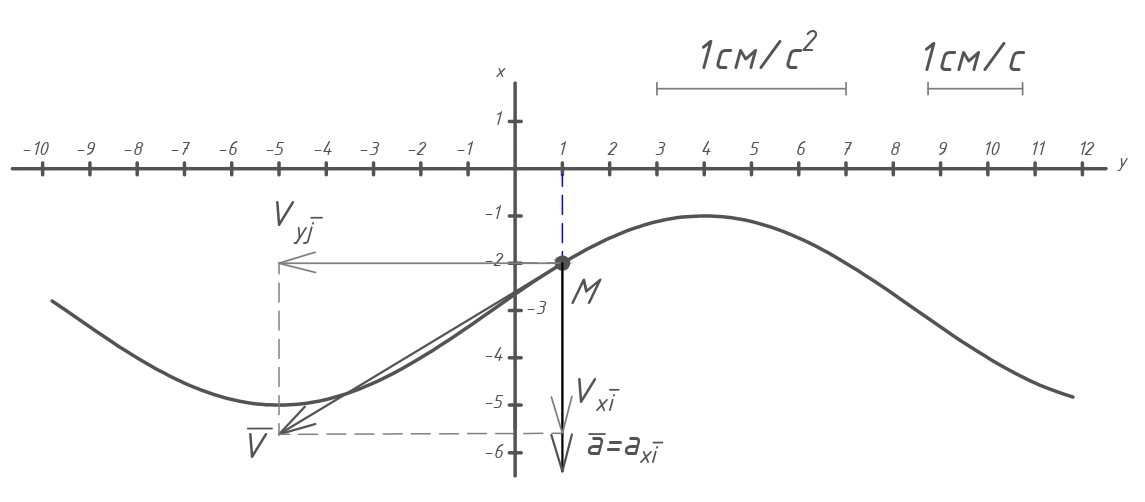 Рис. 4 Вычислим проекцию вектора ускорения на касательную (касательную составляющую вектора ускорения) 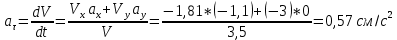 и на главную нормаль (нормальную составляющую вектора ускорения) 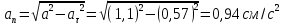 Из формулы нормальной составляющей ускорения точки 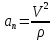 определим радиус кривизны траектории движения точки, для заданного момента времени: определим радиус кривизны траектории движения точки, для заданного момента времени: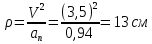 На рис. 5 выполнено разложение вектора ускорения точки на касательную и нормальную составляющие 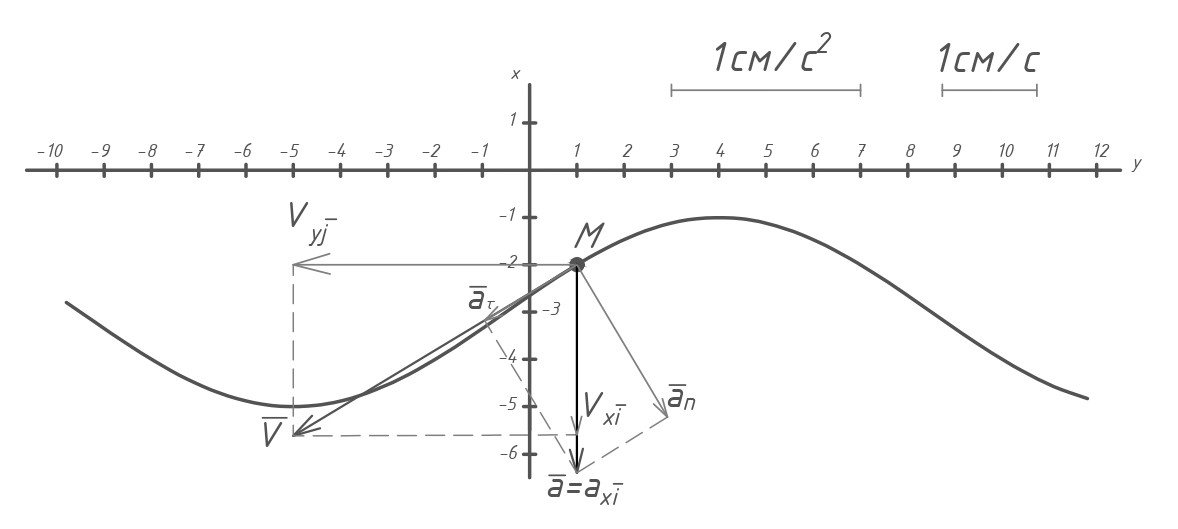 Рис. 5 Ответ: уравнение траектории движения точки 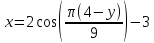 Величина скорости точки 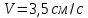 Ускорения точки: полное 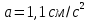 касательное 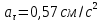 нормальное 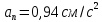 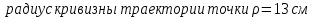 |
