1.Киниматика точек. Задача киниматики. Скорость и ускарение точки. Движение точки в декартовой системе координат. Скорость и ускарение точки в декартах. Векторный способ. Уравнение траектории.
Киниматика точки- движение точки. Задачи: 1.Определить положение движения любого объекта в зависимости от времени. 2. Дать способы определения кинематических характеристик движения (скорость, ускорение). Кинематика занимается нахождением угловой скоростью и ускорением. r=r(t); V=dr/dt=r; ā=dv/dt
x=x(t) vx=x
y=y(t) vy=y
z=z(t) vz=ż
V= √Vx2+Vy2+Vz2 ; ax=Vx=x
a=√ ax2+ay2+az2
ay=Vy=ÿ
az=Vz=z
Уравнение траектории (уравнение кривой в пространнстве)
Если из уравнения движения в декартовой системе координат исключить t, то получим:
F1(x,y,z)=0
F2(x,y,z)=0 ур-ние траектории.
|
2.Естественный способ задание движения. Скорость. Естественные оси координат . Естественные проекции. Ускарение на естественные оси координат.
Задаётся траектория и расстояние точки от начала положения определённого знака наз. дуговой  координатой. координатой.
τ˚- косательная
n˚- главная нормаль
b˚- би нормаль
|V|=|ds/dt|=|S|
|aτ|=|d2s/dt2|=|S|=|V|
an=V2/ρ
ρ- радиус кравизны траектории
V- скорость точки
ab=0
a=√aτ2+an2
|
3.Связь между способами задания движения.
√Vx2+Vy2=|S|
√ax2+ay2+az2=√an2+aτ2
aτ=āv/|v|=axvx+ayvy+azvz/√vx2+vy2+vz2
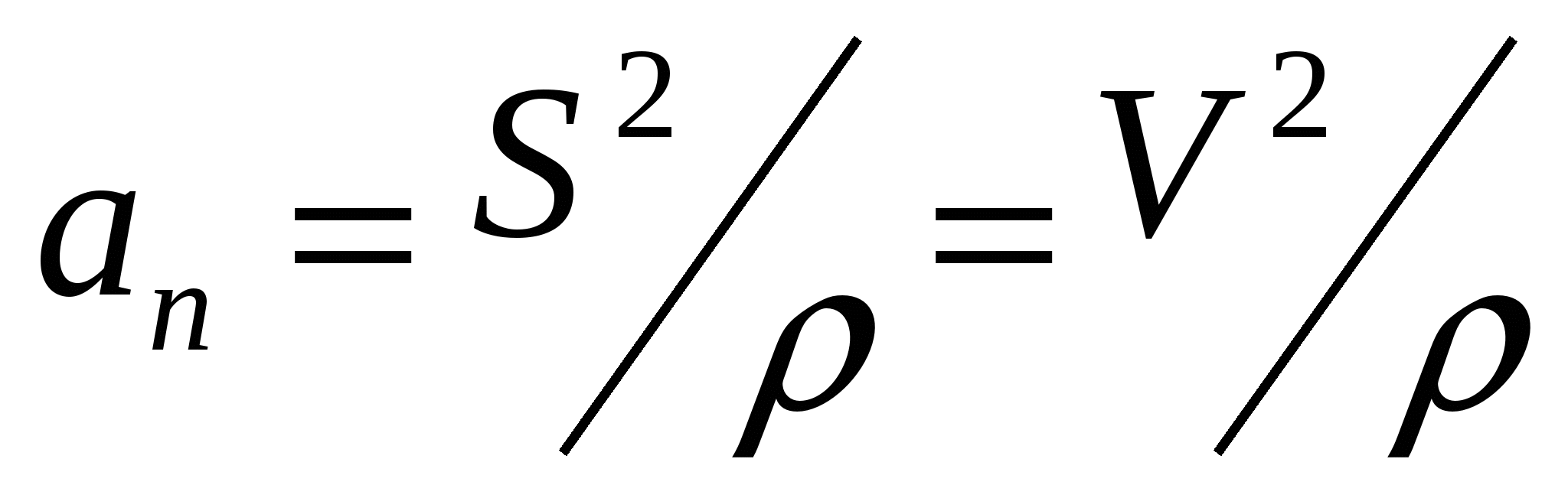
Нормальная составляющая ускорения она хар-ет изменения скорости по направлению
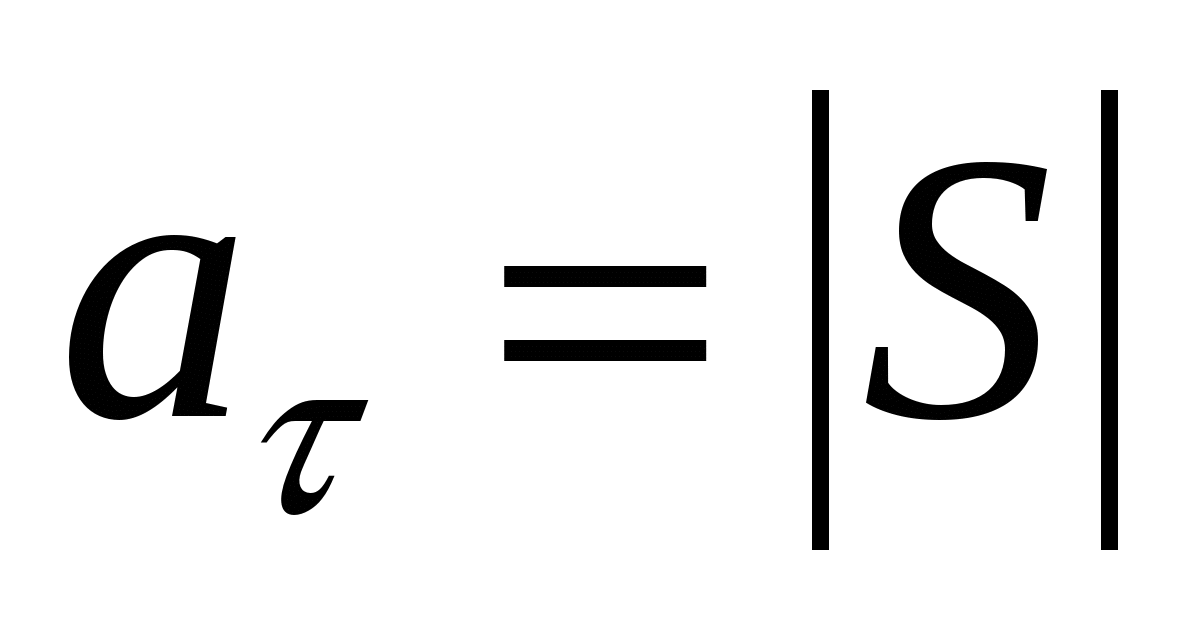 -косат. Составляющая ускорения явл. хар-ной измерения модуля скорости -косат. Составляющая ускорения явл. хар-ной измерения модуля скорости
|
4.Поступательное движение твёрдого тела и его свойства.
Движения тела при котором любая прямая проведённая в нём, движется // первоначально своему начальному движению.
Свойства:
Траектории всех точек одинаковы, скорости и ускорения всех точек тела равны между собой в любой фиксированный момент времени. Для этого для исследования поступательного движения достаточно рассматреть движение любой одной точки.
Вращательное движение твёрдого тела. Уравнение вращательного движеня. Угловая скорость и угловое ускорение, их векторное представление.
Вращательное движение-это движение твёрдого тела у которого две точки закреплены.
φ=φ(t) [Рад]
ω=φ=dφ/dt [c-1]
ε=ω=φ [c-2]
|
5.Скорость и ускарение вращающегося тела.
V=ωh
aτ=εh
an=ω2h
a=h√ε2+ω4 - полное ускорение
v=ωr - векторное представление
ā=εr+ωv скорости и ускорения
|
6.Сложное движение точки. Основные понятия и принцип независимости.
Абсолютное движение- это движение по отношению к неподвижной системе координат. Скорость и ускорение по отношению к этой системе координат.(va,āa)
Относительное движение- это движение по отношению к подвижной системе координат скорости и ускарения (vr, ār)
Переносное движение- это движение, которое сообщает точке подвижная система отсчёта (ve, āe)
Принцип независемости: Если остановлено переносное движение, то абсолютное движение совпадает с относительным.
Если остановлено относительное движение,то абсолютное – совподает с переносным движением.
|
7)Теорема о сложении скоростей при сложном движении
va=ve+vr
vr=s ve=w*r,где r-расстояние от точки до оси вращения
va=√ ve2+ vr2-2 va vrcos30
8)Теорема Кориолиса
aa=ae+ar+ak
aк=2we*vr*sin(we,vr)
arn=0 aen=we2*r
aeτ=eе*r ar=2we*vr*sin90
aax= ar- aensinα+ aeτcosα
|
9)Плоско-параллельное движение твёрдого тела.У-е плоского движения. Теорема о скоростях точек.
Плоско-параллельное движение твёрдого тела-движение при котором траектория любой точки лежит в плоскости параллельной заданной неподвижной плоскости.
Плоско-параллельное движение есть совокупность двух одновременно происходящих движений: поступательного и вращательного вокруг осі перпендікулярной заданной неподвіжной плоскости.
Xa=f1(t)
Ya=f2(t) – у-е плоско-параллельного движения
Φ=f3(t)
Теорема о скоростях: скорость любой точки плоской фигуры равна векторной сумме скорости точки заданной поступательным движением и скорости заданной вращательным движением вокруг полюса.
Мгновенный центр скоростей- это точка скорость которой в данный момент=0
VM=VA+VMA
|
?10) Основные понятия и аксиомы статики. Теорема о переносе силы по линии её действия и уравновешенности 3-х основных сил.
Сила – мера взаимодействия тел или точек. Определяется 3-мя характеристиками: направлением, модулем и точкой приложения.
Система сил – набор сил действующих на одно и тоже тело.
Равнодействующая – одна сила заменяющая систему сил.
Уравновешенная система сил – это система сил под действием которых любое тело находится в равновесии.
Реакции связей – это силы с которыми связи действуют на рассматриваемое тело.
Т1:Любую силу некоторой системы сил можно приложить в любой точке линии её действия и при этом новая система сил будет первоначальной или любую силу можно передвигать вдоль линии и при этом результат неизменится.
Т2: Если известно, что три силы уравновешены то линии их действия пересекаются в одной точке.
|
?11) Момент силы относительно точки. Его представление в виде вектора. Геометрическое представление модуля.
|
12) Момент силы относительно оси.
i j k
m=r*P=x y z
Px Py Pz
m=Ph
mz=xPy-yPx
mz=mcosα
mo=2s⌂OP
mo=Pyx-Pxy
Момент силы относительно оси равен проекции на эту ось вектора момента относительно любой точки лежащей на этой оси. Момент силы относительно оси есть скалярная величина равная произведению проекции силы на плоскость перпендикулярно заданной оси на расстоянии между двумя скрещивающимися прямыми: линии действия силы и заданной осью.
mγ=Pα*h
|
?13) Пара сил и её момент. Теорема о моменте пары.
Две силы равные по модулю и противоположные по направлению линия действия которых не совпадает наз. парой сил.
Момент пары сил не зависит от центра относительно которого он определяется и есть вектор плоскости расположения пары равный по модулю произведению одной из сил пары на расстояние между ними (на ее плечо).
m=Pd
|
?14) Свойства пар сил. Теорема об эквивалентности пар сил.
Две пары сил векторы-моменты которых равны эквивалентны.
Пару сил можно переносить по своей плоскости или в любую параллельную плоскость.
Теорема о сложении пар сил.
Система пар сил может быть заменена эквивалентной ей одной парой сил момент которой равен векторной сумме моментов заданных пар сил.
|
15) Основная теорема статики или приведение системы сил к заданному центру.
Любая система сил может быть заменена системой сил состоящей из двух элементов:1 – одна сила равная векторной сумме заданных сил R|=∑ni=1Pi и наз. главным вектором системы сил, точка приложения её произвольная, которую прінято наз. центром приведения системы сил;2- одна пара сил или просто один момент Mo=m(Q,Q'), который равен векторной сумме моментов заданных сил относительно центра приведения системы сил.
Mo=m(Q,Q')= ∑mo(Pi)
Д-во этой теоремы осуществляется с помощью метода Пуассо: любую силу некоторой системы сил можно приложить в любом заранее выбранном центре на при этом чтобы не изменить результат действия этой системы необходимо добавить пару сил, момент которой равен моменту переносимой силы в центр О относительно этого центра.
R'(Rx,Ry,Rz) R'=√(Rx)2+(Ry)2+(Rz)2
Mo(Mox,Moy,Moz) Mox=∑mx(Pi) и т.п. M0=√M0X2+M0Y2+M0Я2
|
16) Уравнение и условия равновесия:
Р=-Р , {P, P }=0, Mo=0, R'=0, R'=P+P'
Условиями равновесия любой системы сил являются равенство 0 главного вектора и момента. Из этого следует что проекции главного вектора и момента на оси координат должны быть = 0.
Уравнения равновесия при частичном расположении силы.
система сходящихся сил(линии действия которых пересекаются в одной точке). ∑Рix=0, ∑Piy=0, ∑Piz=0
параллельные силы. ∑Piz=0
∑mx(Pi)=0, ∑my(Pi)=0
силы расположены в одной плоскости, тогда уравнения равновесия упростятся, если расположения сил совместить с координатной плоскостью ху.
∑Рix=0, ∑Piy=0, ∑mz(Pi)=0
В этом случае момент сил относительно оси z становиться алгебраической величиной момента сил относительно начальных координат.
|
17) Центр тяжести.
Точка приложения равнодействующих сил тяготения – центр тяжести.
Однородная поле тяготения – это такое поле тяготения при котором напряжённость его есть величина постоянная.
F=G*m1*m2/(r2)
Pi=Δmi*g
Δmi=p*ΔVi
Xc=lim(∑Δmi*g*xi)/(∑Δmi*g)=∫xdV/V
18. Конкретные примеры
Для однородных тел имеющих центр симметрии, ось симметрии или плоскость центр тяжести находится соответственно в центре симметрии, на оси или в плоскости. Исходя из этих свойств, центр тяжести треугольника находится в точке пересечения медиан и т. д.
Если имеется сложное тело, которое составлено или можно разбить на части центры тяжести которых известны:
Xc=(V1*x1+V2*x2+V3*x3)/(V1+V2+V3)
Ecли есть пустоты, то эти обьемы беруться со знаком ‘’-‘’.
|
19) Аксиомы динамики. Основное уравнение динамики материальной точки. Различные формы основного уравнения динамики. Две основные задачи динамики. Решение первой основной задачи динамики.
Ур-ния динамики:
1. ma=∑Pi – основное уравнение динамики в векторной форме
2. mx״=∑Pix
my״=∑Piy
mz״=∑Piz – в декартовой системе координат
3.man=∑Pin
maτ=∑Piτ
mab=∑Pib
Первая задача динамики: задано движение найти силы.(Заданы x(t),y(t),z(t). Вычислить 2-ые производные и подставлять влевую часть основного ур-ия динамики.Решение сводится к определению неизвестных с тремя неизвестными 1-ой степени.)
Вторая задача динамики: заданы силы, определить движения.
|
20) Вторая основная задача динамики точки. Дифференциальные уравнения движения материальной точки. Начальные условия.
Методы решения: разделение переменных, специальные уравнения.
По заданым силам, массе точки, начальным условиям найти движение точки. Диф. ур-ния движение точки: mx״=∑Pix, my״=∑Piy , mz״=∑Piz
Решеніе сводится к решению диф. ур-ний.
Начальные условия: при интегрировании диф.ур-ния второго порядка необходимо определить две произвольные постоянные появляющиеся при этом, для этого необходимо знать начальные условия с какой точки начиналось движение и с какой скоростью.(to=0,x=x0,y=y0,z=z0 и также 1-ые производные)
|
21) Динамика относительного движения материальной точки. Переносная сила инерции и сила Кориолиса. Основное уравнение динамики относительного движения точки.
maa=∑ Pi осн. ур-ніе динамики относительно неподвижной системы координат. Из этого ур-нения возникает необходимость определить движение относительно подвижной неинерциал. системы координат. Абсолютное ускорение заменим ускорение Креалиса:aa=ar+ae+ak
ae-переносное уск., ak- уск. Креалиса, ar- относітельное уск.
mar =∑Pi+(-mae)+(-mak)
Введём обозначение: Фе=-mae, Фк=-mak, которые называются переносная сила инерции, сила инерции Кориолиса.
mar=∑Pi+Фе+Фк – основное уравнение динамики относительного движения и выражает динамическую теорему Кориолиса.
Движение материальной точки по отношению к подвижной неинерциальной системы координат осуществляется реальнодействующими силами Кориолиса и переносной
|
22) Дифференциальные уравнения свободных колебаний материальной точки и его решение. Гармонические свободные колебания. Период, частота и начальная фаза.
Свободные колебания возникают, если на материальную точку действует одна сила.
Fx=-cx, прі t=0 mx״=-cx k=√(c/m) – частота свободных колебаний
τ=2*π/k=2π√(c/m) – период cв. колебаній
х=Asin(kt+α) A=√(x20+(x0/22) – амплитуда
х+(с/m)x=0, α=arctg(kx0/x)-нач. фаза
движения точки, которое она получает под действием восстанавливающей силы наз. Гармоническим колебанием.
x+k2x=0 – каноническое диф.
ур-ие гармонических колебаний
|
23) Механическая система. Внешние и внутренние силы. Свойства внутренних сил. Система уравнений движения точек механической системы. Центр масс механической системы и теорема о движении центра масс.
Механическая система – это совокупность материальных точек взаимодействующих между собой таким образом, что движение каждой из них определяется движением всех остальных.
Внешние силы – это силы, действующие со стороны объектов, не входящих в эту систему. Рie-равнодействующая всех внешніх сил приложеных к точке i.
Внутренние силы – это силы взаимодействия между точками заданной системы.Pij- равнодействующая всех внутренніх сіл приложеных к точке i.
Свойство внутренних сил:
1.Сумма внутренних сил =0 и сумма их моментов относительно любого центра =0.∑Рiα=0,∑m0(Piα)=0. Для каждой матер. точкі mi можно записать осн.ур-ние динамики: miai= Рie+.Pij – ур-ніе движ. точек мех. системы.
2.Центр масс механической системы – точка положение которой определяется по формуле:
Rc=∑mi*ri/∑mi хс=∑miхi/∑mi
Теорема: Движение центра масс могут изменить только внешние силы.
Следствие: если сумма внешних сил =0, то центр масс находится в покое или движется равномерно и прямолинейно.
|
24) Количество движения материальной точки и механической системы. Теорема об внутреннем количестве движения. Импульс силы. Теорема об изменении количества движения материальной точки.
Количество движения есть вектор определяемый по формуле: qi=mivi, где mi- масса, vi- скорость.
Кол-во движения системы – есть вектор равный сумме кол-в движения его точек. Q=∑qi=∑ mivi
Теорема:Кол-во движения механической системы равно кол-ву движения материальной точки совпадающей с центром масс и массой равной массе всей системы.Q=mvc
Импульсы силы – это характеристика её действия в зависимости от времени и определяется формулой: S̃(t)=∫Fdt
Теорема об изменении кол-ва движения: производная по времени от кол-ва движения механической системы равна сумме векторов внешних сил действующих на эту систему:
dQ/dt=∑Pie или изменение кол-ва движения за некоторое время равна сумме импульсов внешних сил.
Q̃2-Q̃1=∑P̃ie
Следствие: з-н сохранения кол-ва движения: если сумма внешних сил равна 0, то кол-во движения постоянно.
|
25) Момент инерции относительно оси. Ф-лы моментов инерции относительно координатных осей. Теорема о моментах инерции относительно параллельных осей.
Момент инерции твёрдого тела относительно оси – скалярная величина определённо положительная и определяемая по формуле: Ij=∑mihi2, где h – расстояние от точки до заданной оси, mi- масса точки. [кг*м2]
Ix=∑mi(yi2+zi2)
Iy=∑mi(xi2+zi2)
Iz=∑mi(yi2+zi2)
Теорема Гюйгенса-Штейнера: Iγ=Iγc+md2
Момент інерціі относительно произвольной оси равняется сумме моментаинерции относительно оси \\-о заданой и проходящей через центр масс и произвольно массе тела на квадрат расстояния между осями.
|
26) Момент кол-ва движения материальной точки. Кинетический момент относительно центра и оси. Формулы их относительно координатных осей.
Момент кол-ва движения есть вектор определяемый по формуле: |i j k |
loi=rimi*vi=|x y z|mi
|x΄ y΄ z΄|
Момент кол-ва движения относительно оси – скалярная величина равная проекции на эту ось вектора момента кол-ва движения относительно любой точки на заданной оси.
Формулы кол-ва движения относительно координатных осей:
lix=(yiz΄-ziy΄)mi
liy=(zix΄-xiz΄)mi
liz=(xiy΄-yix΄)mi
кинетический момент механической системы – это есть вектор Lo равный сумме моментов кол-в движений каждой точки:
Lo=∑loi
Lx=∑mi(yiz΄-ziy΄)
Ly=∑mi(zix΄-xiz΄)
Lz=∑mi(xiy΄-yix΄)
|
27) Формула кинетического момента вращающегося твёрдого тела относительно оси его вращения. Теорема об изменении кинетического момента и следствие из неё.
vi=whi Liz=Iz*w, где Iz – момент инерции относительно оси вращения.
Iz=∑Δmih2 Lz=∑Δmivihi
Теорема об изменении кинетического момента:
Производная от кинетического момента по времени равна сумме моментов внешних сил. Pie-внешние силы
dLo/dt=∑mo(Pie)
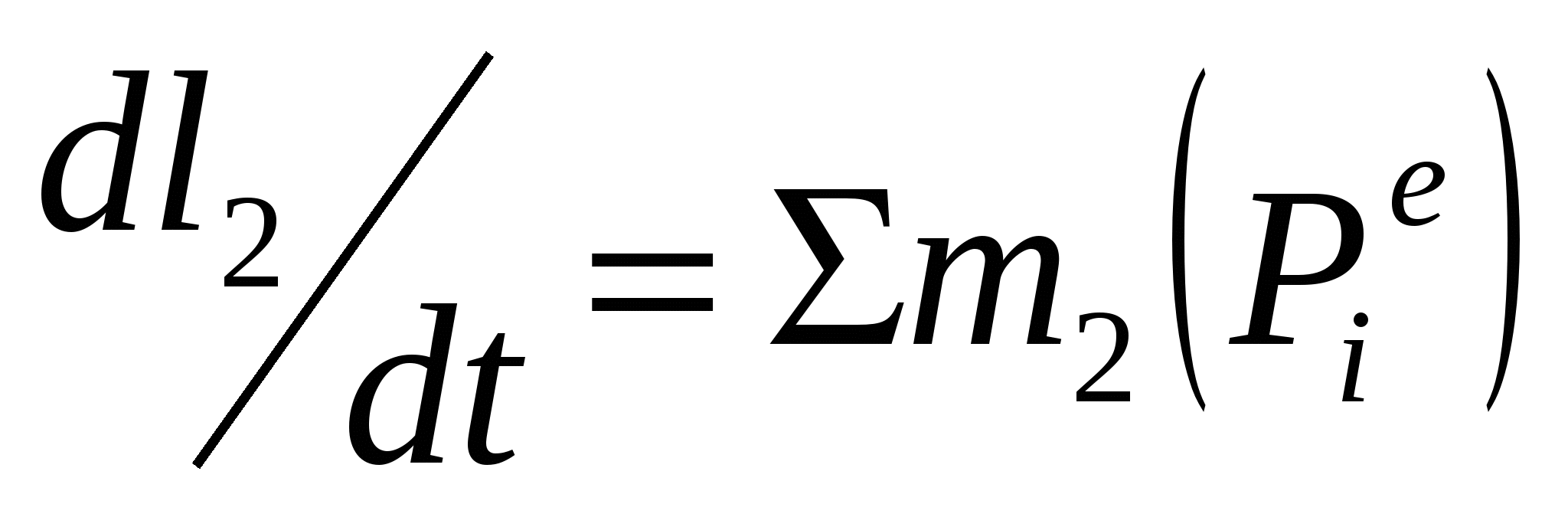 -в проекции на ось координат -в проекции на ось координат
Следствие1: основное уравнение вращательного движения d(Izw)/dt=∑mz(Pie)
В частном случае когда вращается твёрдого тела относительно неподвижной оси, тогда момент инерции не меняется.
Iz*dw/dt=∑mz(Pie) осн. ур-ніе Izε=∑mz*(Pie) динамики вращ. движ.
Следствие2: закон сохранения кинетического момента.
Если сумма моментов внешних сил относительного какого-нибудь центра или оси =0, то соответствующий кинетический момент есть величина постоянная.
∑mz*(Pie)=0, Lz-const.
|
28) Работа и мощность силы, элементарная работа. Работа силы тяжести и силы упругости. Работа сил приложенных к твёрдому телу.
Элементарная работа – скалярная величина равная работе силы на бесконечно малом перемещении точки её приложения и определяемая по формуле:
dA=F̃*dr= Fxdx+Fydy+Fzdz, где Fx, Fy, Fz –проекции сил на оси координат, dx, dy, dz – приращение соответствующих координат точек приложения.
Для определения работы на конечном перемещении точки приложения силы необходимо просуммировать элементарную работу: A=∫F̃dr
Мощность силы – это есть производная по времени от работы.
Работа силы трения и силы упругости не зависит от формы траектории точки приложения этих сил и определяется: A=-mgΔh (сила тяжести)
A=c/2*(Δl12+Δl22) – (сила упругости)
Где с – коэффициент жёсткости упругой силы, Δl1, Δl2 – расстояние точки приложения силы от той точки, где эта сила обращается в 0.
Работа сил приложенных к твёрдому телу.
При вращательном движении твёрдого тела работа сил приложенных к телу определяется по формуле: A=∫Mzedφ, где Mze – сумма моментов внешних сил относительно оси вращения, φ – угол поворота тела.
Мощность в этом случае: Mzeω– угловая скорость тела.
|
29) Кинетическая энергия тела материальной точки механической системы. Формулы кинетической энергии при поступательном, вращательном и плоско-параллельном движении. Теорема об изменении кинетической энергии.
Кинетическая энергия материальной точки – это скалярная величина определяемая по формуле: Ti=1/2mivi2
Кинетическая энергия механической системы – это энергия равная сумме кинетических энергий точек входящих в эту систему.
При поступательном движении формула кинетической энергии аналогична формуле для материальной точки: T=1/2mivc2
При вращательном движении кинетическая энергия определяется по формуле: Ti=1/2*Izw2
Так как плоско-параллельное движение совокупность этих движений:
Ti=1/2*mv2+1/2*Izcw2
Теорема: производная по времени от кинетической энергии равна мощности всех сил: dT/dt=N
Изменение кинетической энергии за некоторое время равно работе всех сил за это же время:
Т-То=А
dT/dt=d/dt(1/2Izω2)=Izωε=Mzeω=N
|
30) Принцип Даламбера материальной точки и механической системы. Приведение сил инерции.
Запишем основное уравнение динамики в виде: ∑Р̃+(-ma)=0
-ma=Ф – сила инерции
Основное уравнение динамики примет вид: ∑Р̃+Ф̃=0, что и позволило Даламберу сформулировать свой принцип: если ко всем точкам механической системы приложить силы инерции, то полученная система сил будет взаимно уравновешенной и для нее можно составить уравнение равновесия из статики, которые называются динамическими уравнениями равновесия.
Главный вектор или сумма всех сил инерции равен силе инерции материальной точки совпадающей с центром масс механической системы, масса которой равна массе всей системы. RФ=∑Фi=-mac
Главный момент сил инерции при вращательном движении твёрдого тела относительно оси его вращения определяется формулой Mzф=-Izε, где Mzф=∑mz(Ф̃) – главный момент сил инерции. Iz-момент инерции относительно оси вращения, ε- угловое ускорение.
|
 Скачать 116 Kb.
Скачать 116 Kb.