Социализация. Движение точки задано координатным способом на плоскости
 Скачать 77.95 Kb. Скачать 77.95 Kb.
|
|
Движение точки задано координатным способом на плоскости 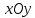 . Следует найти траекторию точки и построить ее на рисунке. Скорость, полное ускорение и касательное ускорение найти как функцию времени. Скорость, ускорение, касательное ускорение, нормальное ускорение и радиус кривизны траектории определить в момент времени . Следует найти траекторию точки и построить ее на рисунке. Скорость, полное ускорение и касательное ускорение найти как функцию времени. Скорость, ускорение, касательное ускорение, нормальное ускорение и радиус кривизны траектории определить в момент времени 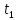 . Векторы . Векторы 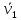 , , 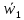 , , 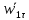 , , 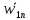 показать на рисунке. показать на рисунке.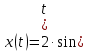 м; м; 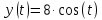 м; м; 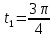 с. с.Координаты точки: в начальный момент движения 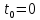 точка точка 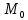 : :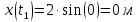 ; ;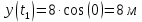 . .в заданный момент времени 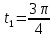 точка точка 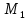 : :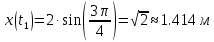 ; ;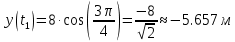 . .Исключим из заданных уравнений параметр 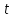 : :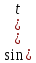 , , 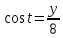 , , 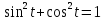 , следовательно, , следовательно, 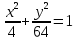 - уравнение эллипса. - уравнение эллипса.Из условий 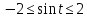 и и 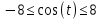 следует, что траекторией будет эллипс, заключенный в этих интервалах. следует, что траекторией будет эллипс, заключенный в этих интервалах.Скорость Проекции вектора скорости на оси координат: 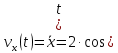 ; ; 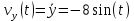 Проекции вектора скорости в заданный момент времени: 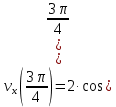 ; ; 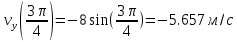 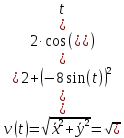 ; ;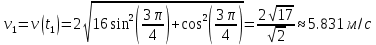 . .Ускорение Направим ось τ в сторону движения точки, найдем касательное ускорение: 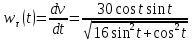 ; ;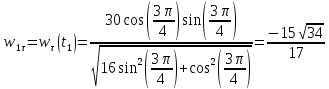 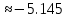 м/c2 м/c2Проекции ускорения на оси координат: 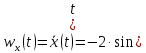 м/c2; м/c2; 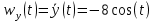 м/c2; м/c2;В заданный момент времени: 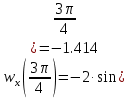 м/c2; м/c2; 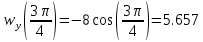 м/c2; м/c2;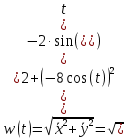 ; ;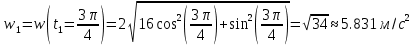 . .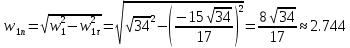 м/с2 м/с2Радиус кривизны в момент времени 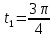 с с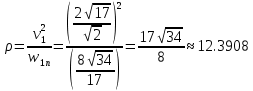 м м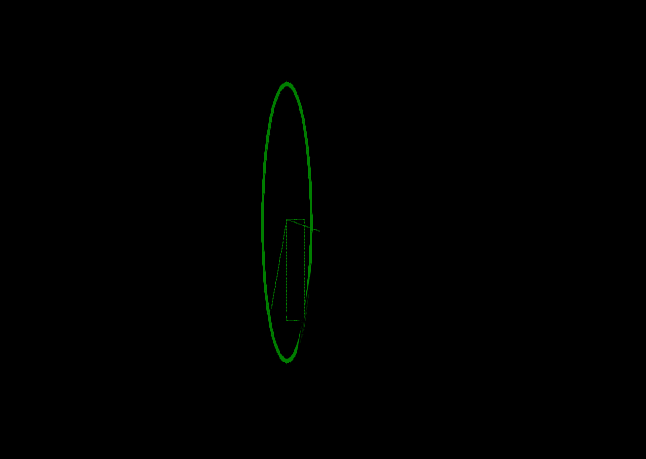 |
