Лекция 23 Тема теоремы об изменении количества движения точки и системы цель лекции План лекции
 Скачать 120.72 Kb. Скачать 120.72 Kb.
|
|
ЛЕКЦИЯ № 23 Тема: ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ И СИСТЕМЫ Цель лекции: План лекции: Количество движения материальной точки и механической системы Элементарный и полный импульс силы Теоремы об изменении количества движения точки и системы. Пример 1. Количество движения материальной точки и механической системы Количеством движения материальной точки называется векторная величина 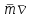 , равная произведению массы точки на ее скорость. Направлен вектор , равная произведению массы точки на ее скорость. Направлен вектор 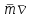 так же, как и скорость точки, т. е. по касательной к ее траектории. Единицей измерения количества движения является в СИ — 1 кг·м/с=1 Н·с. так же, как и скорость точки, т. е. по касательной к ее траектории. Единицей измерения количества движения является в СИ — 1 кг·м/с=1 Н·с.Количеством движения системы будем называть векторную величину 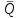 , равную геометрической сумме (главному сектору) количество движения всех точек системы (рис. 23.1): , равную геометрической сумме (главному сектору) количество движения всех точек системы (рис. 23.1):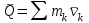 . (23.1) . (23.1)Пользуясь этим определением, найдем формулу, с помощью которой значительно легче вычислять величину 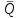 , а также уяснить ее смысл. Из равенства центра масс следует, что , а также уяснить ее смысл. Из равенства центра масс следует, что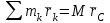 . .Беря от обеих частей производную по времени, получим 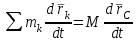 или или 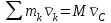 . .Отсюда находим, что 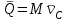 , (23.2) , (23.2)т. е. количество движения системы разно произведению массы всей системы на скорость ее центра масс. Этим результатом особенно удобно пользоваться при вычислении количеств движения твердых тел. 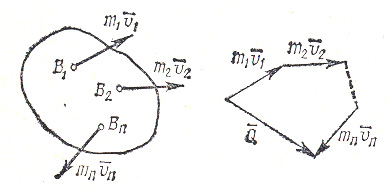 Рис. 23.1 Из формулы (23.2) видно, что если тело (или система) движется так, что центр масс остается неподвижным, то количество движения тела равно пулю. Например, количество движения тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс, будет равно нулю. Если же движение тела является сложным, то величина 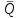 не будет зависеть от его вращательного движения вокруг центра масс. не будет зависеть от его вращательного движения вокруг центра масс.Например, для катящегося колеса 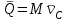 , независимо от того, как вращается колесо вокруг его центра масс С. , независимо от того, как вращается колесо вокруг его центра масс С.Таким образом, количество движения можно рассматривать как характеристику поступательного движения системы (тела), а при сплошном движении — как характеристику поступательной части движения вместе с центром масс. 2. Элементарный и полный импульс силы Импульс силы. Для характеристики действия, оказываемого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Сначала введем понятие об элементарном импульсе, т. е. об импульсе за элементарный промежуток времени dt. Элементарным импульсом силы называется векторная величина 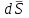 , равная произведению силы , равная произведению силы 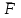 на элементарный промежуток времени dt: на элементарный промежуток времени dt: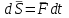 . (23.3) . (23.3)Направлен импульс вдоль линии действия силы. Импульс 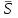 любой силы любой силы 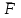 за конечный промежуток времени t1 вычисляется через интеграл: за конечный промежуток времени t1 вычисляется через интеграл: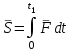 . (23.4) . (23.4)В частном случае, если сила 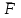 постоянна и по модулю, и по направлению ( постоянна и по модулю, и по направлению (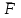 =const), то =const), то 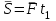 . В общем случае модуль импульса может быть вычислен по его проекциям на координатные оси: . В общем случае модуль импульса может быть вычислен по его проекциям на координатные оси: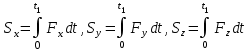 . (23.5) . (23.5)Единицей измерения импульса силы, как и количества движения, является в СИ — 1 кг м/с. 3. Теоремы об изменении количества движения точки и системы. 1. Теорема об изменении количества движения точки Так как масса точки постоянна, а ее ускорение 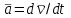 , то уравнение, выражающее основной закон динамики, можно представить в виде , то уравнение, выражающее основной закон динамики, можно представить в виде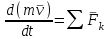 . (23.6) . (23.6)Уравнение (23.6) выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил. Пусть движущаяся точка имеет в момент времени t=0 скорость 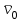 , а в момент t1 — скорость , а в момент t1 — скорость 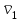 . . 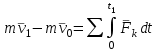 . (23.7) . (23.7)Стоящие справа интегралы, как следует из формулы (23.7), представляют собой импульсы действующих сил. 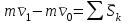 . (23.8) . (23.8) Уравнение (23.8) выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени. При решении задач вместо векторного уравнения (23.8) часто пользуются уравнениями в проекциях. 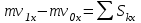 (23.9) 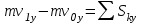 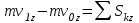 2. Теорема об изменении количества движения системы Рассмотрим систему, состоящую из п материальных точек. Составим для этой системы дифференциальные уравнения движения (20.3) и сложим их почленно. Тогда получим 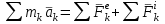 . .Последняя сумма по свойству внутренних сил равна нулю. Кроме того, 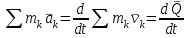 Окончательно находим 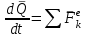 (23.10) (23.10)Уравнение (15.15) выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил. В проекциях на координатные оси будет: 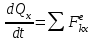 , , 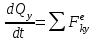 , , 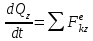 . (23.11) . (23.11)Найдем другое выражение теоремы. Пусть в момент времени t=0 количество движения системы равно 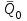 , а в момент t1 становится равным , а в момент t1 становится равным 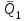 . Тогда, умножая обе части равенства (23.10) на dt и интегрируя, получим . Тогда, умножая обе части равенства (23.10) на dt и интегрируя, получим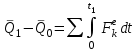 или 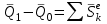 (23.12) (23.12)так как интегралы, стоящие справа, дают импульсы внешних сил. Уравнение (23.12) выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени. Укажем на связь между доказанной теоремой и теоремой о движении центра масс. Так как 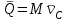 , то, подставляя это значение в равенство (23.10) и учитывая, что , то, подставляя это значение в равенство (23.10) и учитывая, что 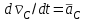 , получим , получим 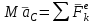 , т. е. уравнение (22.3). , т. е. уравнение (22.3).Следовательно, теорема о движении центра масс и теорема об изменении количества движения системы представляют собой, по существу, две разные формы одной и той же теоремы. В тех случаях, когда изучается движение твердого тела (или системы тел), можно в равной мере пользоваться любой из этих форм, причем уравнением (15.15) обычно пользоваться удобнее. Для непрерывкой же среды (жидкость, газ) при решении задач обычно пользуются теоремой об изменении количества движения системы. Важные приложения эта теорема имеет также в теории удара и при изучении реактивного движения. Практическая ценность теоремы состоит в том, что она позволяет исключить из рассмотрения наперед неизвестные внутренние силы (например, силы давления друг на друга частиц жидкости). 3. Закон сохранения количества движения Из теоремы об изменении количества движения системы можно получить следующие важные следствия. 1. Пусть сумма всех внешних сил, действующих на систему, равна нулю: 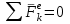 . .Тогда из уравнения (22.10) следует, что при этом 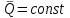 . Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению. . Таким образом, если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению.2. Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например, Ох) равна нулю; 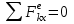 . .Тогда из уравнений (22.11) следует, что при этом Qx=соnst. Таким образом, если сумма проекций всех действующих внешних сил на какую-нибудь ось равна нулю, то проекция количества движения системы на эту ось есть величина постоянная. Эти результаты и выражают закон сохранения количества движения системы. Из них следует, что внутренние силы изменить количество движения системы не могут. При решении задач применение теоремы позволяет исключить из рассмотрения все внутренние силы. Поэтому рассматриваемую систему надо стараться выбирать так чтобы все (или часть) заранее неизвестных сил сделать внутренними. Закон сохранения количества движения удобно применять в тех случаях, когда по изменению поступательной скорости одной части системы надо определить скорость другой части. В частности, этот закон широко используется в теории удара. Пример: По шероховатой наклонной плоскости, составляющей с горизонтом угол =30, спускается тяжёлое тело без начальной скорости. Определить в течение какого времени Т тело пройдёт путь, длиной 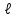 = 39.2 м, если коэффициент трения f = 0.2. = 39.2 м, если коэффициент трения f = 0.2.Решение: 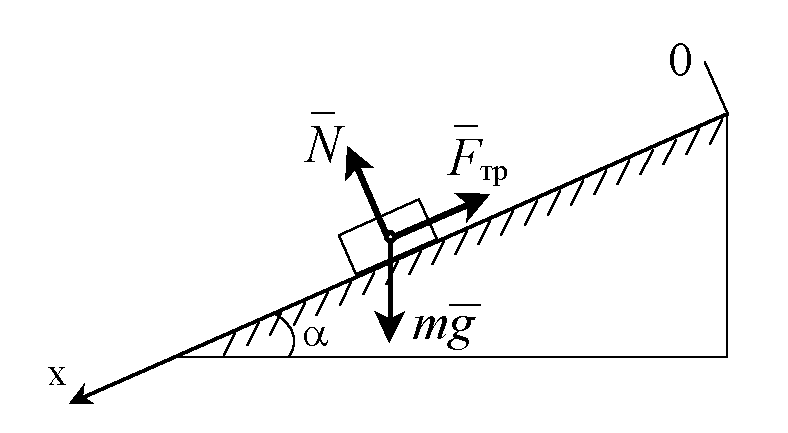 Рисунок 35.3. Изобразим на чертеже силы, приложенные к грузу: вес груза – 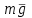 нормальную реакцию поверхности – нормальную реакцию поверхности – 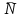 , сила трения – , сила трения – 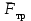 , причём , причём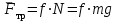 Направим ось x вдоль наклонной плоскости в сторону движения вниз. Запишем теорему об изменении количества движения в проекциях на ось x: 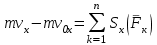 (*) (*)Согласно условию задачи 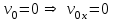 , ,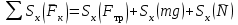 . .Вычислим импульсы каждой силы, учтя, что все действующие на тело силы постоянны. 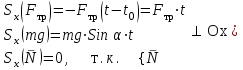 Тогда  . .Подставим это выражение в (*): 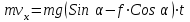 или или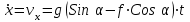 Проинтегрируем это уравнение по времени t: 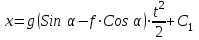 , ,C 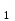 определим из начальных условий: при t = 0, х = 0 С1 = 0. определим из начальных условий: при t = 0, х = 0 С1 = 0.Итак, закон движения тела имеет вид: 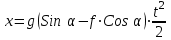 Для того, чтобы определить время Т, за которое время пройдёт путь 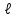 = 39.2 м, подставим эти значения в уравнение движения: = 39.2 м, подставим эти значения в уравнение движения: 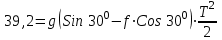 Откуда 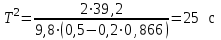 . Ответ: . Ответ: 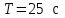 . .Цифровые образовательные ресурсы (цифровые учебные материалы) Теорема об изменении момента количества движения (заимствованный видео материал, https://www.youtube.com/watch?v=cUwMXB5nPdA Закон сохранения количества движения системы https://www.youtube.com/watch?v=hWyQYEIOLOg |
