Математика. Практическая работа отпр. Решение Для получения уравнения изоклин положим, тогда 2x(1y) k Возьмем 3 изколины при k 2,1,0,1,2
 Скачать 123.28 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА Группа Студент МОСКВА 2021 Задание 1.Дано: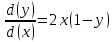 Решение:Для получения уравнения изоклин положим 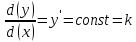 , тогда 2x(1-y) =kВозьмем 3 изколины при k = -2,-1,0,1,2; k=0 => 2x(1-y) = 0 k=-2 => 2x(1-y) = -2 k=-1 =>  k=1 => 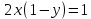 k=2 => 2x(1-y) = 2 Построим изоклины и интегральные прямые: Ответ: Задание 2.Дано: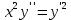 Решение:Сделаем подстановку: y’ = u Получим 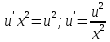 Преобразуем   Проинтегрируем обе части: 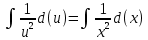 Вычисляем полученные интегралы: 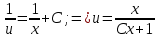 Обратная замена: u = y’;  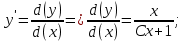 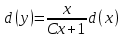 Проинтегрируем обе части: 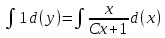 Получим:  Ответ: Задание 3.Дано: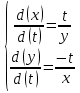 Решение: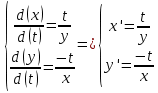 Сведем систему к одному уравнению  Получим: 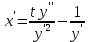 Подставим значения x и x’ в 1-е уравнение системы:  Однородное уравнение относительно y, сделаем подстановку:  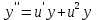 Получим:  Преобразуем  :   Проинтегрируем обе части  Получим:  Возведем в степень и получим: 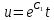 Вычесленное ОДУ: 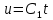 Обратная замена: 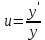 Получим  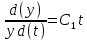  Проинтегрируем: 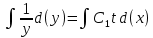 Получим  Возведем в степень 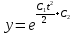 Вычисленное решение ОДУ 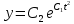 Подставим в уравнение  ; y и получим: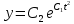 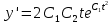 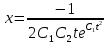 Ответ: 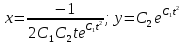 Задание 4.Дано:Вероятность появления события в каждом из п независимых испытаний равна 0,7. Сколько нужно произвести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение:По условию р = 0,7; поэтому q = 1- 0,7 = 0,3. Наивероятнейшее число появлений события т0 =10. Требуется найти число испытаний n. 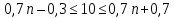 Получим: 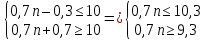 =>  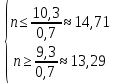Ответ: необходимо произвести ровно 14 испытаний, чтобы наивероятнейшее число появлений события равнялось 10 |