компрессоры ГТД. 3 задачи +. Решение для решения задачи воспользуемся правилом Жуковского
 Скачать 49.31 Kb. Скачать 49.31 Kb.
|
|
№1(15) Самолет делает правый разворот. Ротор двигателя вращается влево. Определить направление действия гироскопического момента и воздействие его на самолет. Решение: для решения задачи воспользуемся правилом Жуковского. 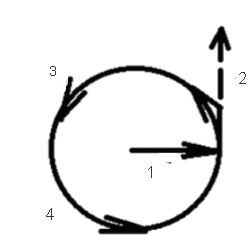 Изобразим плоскость вращения ротора двигателя окружностью 4. Направление вращения ротора стрелками 3 по окружности. Если стрелку 1 провести из центра окружности, в направлении движения носа самолета, а стрелку 2 по касательной к окружности в направлении вращения ротора двигателя, то эта стрелка 2 покажет дополнительное движение носа самолета, вызванное действием гироскопического момента двигателя. Т.е. при правом развороте, и вращении ротора двигателя влево, самолет будет уводить вверх. Вопрос к задаче: Гироскопический момент. Ответ: Гироскопические моменты, как известно, появляются при изменении положения оси вращения тела. Происхождение этих моментов можно показать на следующем простом примере. Пусть две массы m1 и m2, соединенные стержнем, вращаются вокруг оси Ох с некоторой угловой скоростью y (рис. 1,а). Попытаемся изменить положение оси вращения, создав в момент прохождения стержнем горизонтального положения кратковременным импульсом угловую скорость y. В результате этого масса т1 приобретет дополнительную скорость ∆V1 направленную вперед, а масса m2 - скорость ∆V2, направленную назад. При дальнейшем вращении системы с угловой скоростью x массы m1 и m2, стремясь по инерции сохранить приобретенные скорости, создадут гироскопический момент Мгир, который при переходе из положения а в положение б (рис. 1, б) будет стремиться повернуть ось Ох вокруг оси Oz. Таким образом, гироскопический момент появляется при вращении тела вокруг двух осей и действует относительно третьей, им перпендикулярной, аналогично тому, как это имеет место у гироскопа. Вращающийся ротор компрессора и газовая турбина реактивного двигателя представляют собой большие гироскопы, установленные на самолете. Такой гироскоп, укрепленный на самолете, имеет три степени свободы. Во-первых, он может вращаться вокруг собственной оси, которую обычно считают совпадающей со связанной осью Ox1. Во-вторых, гироскоп может вращаться вместе с самолетом вокруг взаимно перпендикулярных осей Оу1 и Oz1. 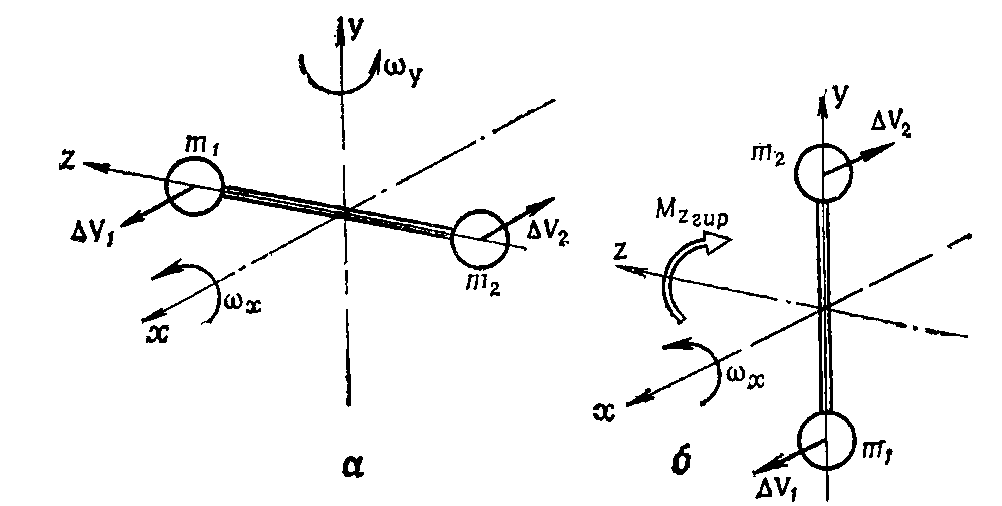 Рис. 1. Возникновение гироскопического момента. Величина гироскопического момента ротора двигателя определяется по формуле: Мгир=Jрр, Где Jр - момент инерции ротора двигателя; р и - соответственно угловые скорости вращения собственно ротора двигателя и вращения самолета вокруг оси, не совпадающей с осью вращения ротора двигателя. Направление гироскопического момента удобно определить, воспользовавшись следующим мнемоническим правилом. Представим себя сидящими в кабине самолета. Плоскость вращения ротора двигателя изобразим окружностью, а направление вращения ротора стрелками по окружности (рис. 2). Если из центра окружности провести одну стрелку (1) в направлении движения носа самолета при вращении с угловой скоростью у, а другую (2) по касательной к окружности в направлении вращения ротора двигателя, то эта стрелка (2) покажет направление дополнительного (прецессионного) движения носа самолета, вызванного действием гироскопического момента ТРД. Так, например, при левом вращении ротора двигателя и принудительном развороте носа самолета влево появится гироскопический (пикирующий) момент, который будет стремиться опустить нос самолета (рис. 2). Самолет, вращающийся с некоторой угловой скоростью относительно одной из осей координат, также можно рассматривать как некоторый гироскоп, который, сопротивляясь изменению положения оси вращения, создает гироскопический (инерционный) момент. В самом деле, представим распределение масс в самолете схематически в виде двух сосредоточенных масс, разнесенных вдоль фюзеляжа (рис. 3). Предположим, что у самолета, вращающегося вокруг оси Ох1 с угловой скоростью х, летчик «дачей» правой ноги (отклонением руля направления вправо) создал вращение самолета вокруг оси Оу1 с угловой скоростью у. Одновременное вращение самолета с угловыми скоростями х и у эквивалентно вращению самолета вокруг некоторой оси а-а с угловой скоростью . Так как сосредоточенные массы m1 и m2 расположены не на этой оси вращения, появятся центробежные силы F1 и F2. Они создадут относительно центра тяжести самолета инерционный (гироскопический) момент вокруг оси Oz1 который, как это видно из рис. 3, стремится поднять нос самолета и увеличить угол атаки. Величина продольного (инерционного) момента МZин определяется следующим выражением: МZин=(Jх-Jу)ху,(4.12) Где Jх и Jу - моменты инерции относительно осей Ox1 и Oy1; х и у - угловые скорости вращения самолета относительно осей Ox1 и Oy1. Можно показать, что при вращении самолета вокруг оси, не совпадающей с одной из связанных осей, кроме продольного инерционного момента, возникают инерционные моменты рыскания крена: Мyин=(Jz-Jx)zx (4.13) Мxин=(Jy-Jz)yz (4.14) Как видно, инерционные моменты пропорциональны произведению угловых скоростей на разность моментов инерции: Jx–Jy, Jz–Jx, Jy-Jz. В отличие от восстанавливающих (стабилизирующих) моментов, обеспечивающих возвращение самолета к исходному режиму полета, инерционные моменты являются дестабилизирующими, стремящимися увести самолет от заданного режима полета. 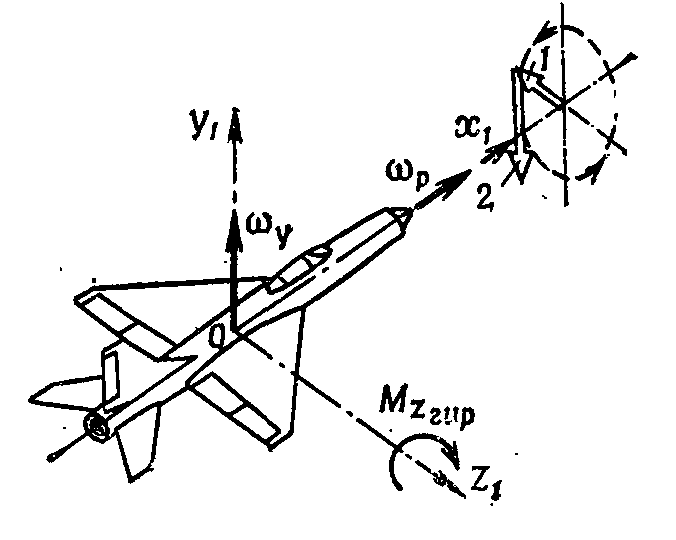 Рис. 2. определение направления дествия гироскопического момента ротора двигателя. 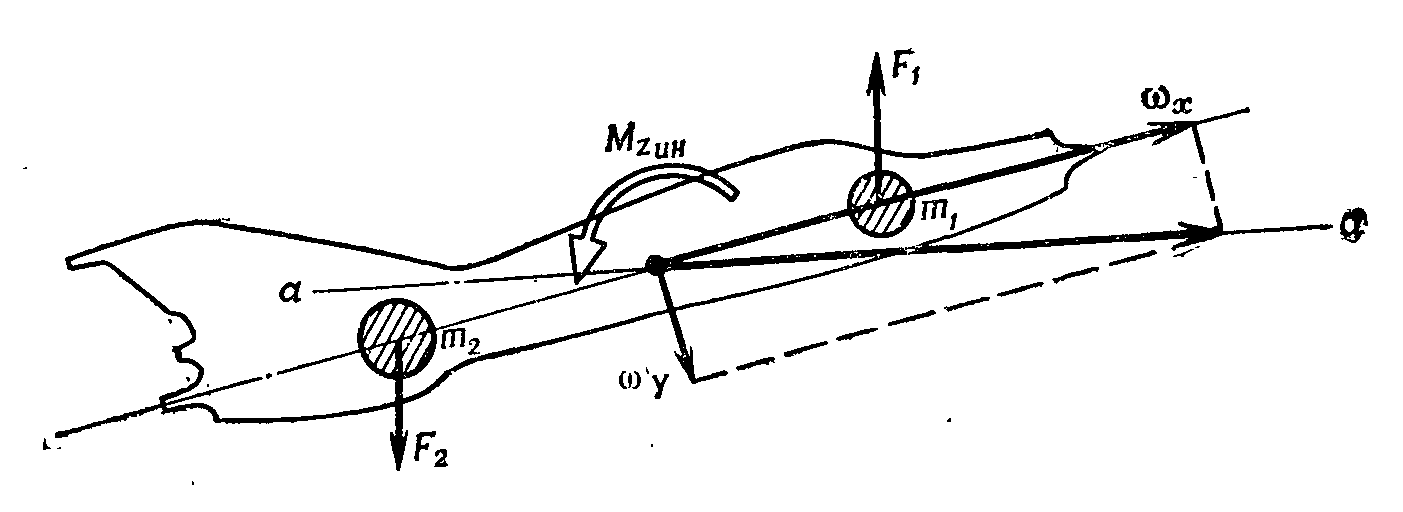 Рис. 3. Появление продольного инерционного момента. №2(15) Определить неуравновешенную центробежную силу, если масса ротора 500 кг, частота вращения ротора 4700 об/мин, эксцентриситет е = 0,02 мм. №3(18) Определить действительную объемную подачу шестеренного масляного насоса, если число зубьев шестерни Z = 12, модуль m = 3,5, высота зубьев h = 8 мм, длина зуба в = 10мм, частота вращения вала насоса n = 3500 об/мин. Коэффициент подачи насоса ƞv= 0,82. Учеба https://yadi.sk/d/CXr3ch9fGB8j8A |
