Статистика Практическое задание 2. Решение Для того чтобы вычислить среднее значение признака перейдем от интервального ряда к дискретному, т е. найдем середину каждого интервала как полусумму нижней и верхней границ.
 Скачать 45.94 Kb. Скачать 45.94 Kb.
|
|
Задание 1 В целях изучения стажа рабочих завода проведена 36%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
На основе этих данных вычислите: 1) средний стаж рабочих завода; 2) моду и медиану стажа рабочих; 3) средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации; 4) с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих всего завода; Решение: 1. Для того чтобы вычислить среднее значение признака перейдем от интервального ряда к дискретному, т.е. найдем середину каждого интервала как полусумму нижней и верхней границ. При этом величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы – к величине интервала предпоследней группы. Для удобства вычислений составляем таблицу.
Найдем средний стаж: 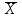 = = 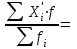 1380/100=13,8 лет 1380/100=13,8 лет2. Найдем моду Мо и медиану Ме: Мо=ХМо + iМо  лет летfM0,fM0-1,fM+1 –частоты модального ,до и после модального интервалов соответственно,ХМ0 – начало модального интервала. iМО- величина модального интервала. Мода показывает варианту наиболее часто встречающегося в данной совокупности, т.е. наиболее часто встречающийся стаж рабочих в данной совокупности равен 16,18% Ме=ХМе + iМе  лет летХМе- начало медианного интервала; iМе - величина медианного интервала; SМе- сумма накопленных частот до медианного интервала: fМе – частота медианного интервала. Медиана – это варианта, располагающаяся в середине ранжированного ряда распределения. Вывод: половина рабочих имеет стаж до 14,167 лет, а вторая половина рабочих – более 14,167 лет. 3. Найдем дисперсию по следующей формуле: 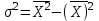 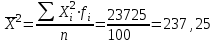  237,25-13,82 =46,81 237,25-13,82 =46,81Дисперсия показывает среднее арифметическое квадратов отклонений каждого значения признака от средней арифметической. Среднее квадратическое отклонение находим по специальной формуле:  = 6,84 лет = 6,84 летКоэф. вариации 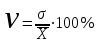 = (6,84/13,8) ·100%=50% = (6,84/13,8) ·100%=50%Когда относительные показатели вариации не превышают 35%, то принято считать, что полученные средние характеристики достаточно надежно характеризуют совокупность по варьирующему признаку. В нашем же случае, напротив, коэффициент вариации больше 35% -- не надежно, т.е. полученный средний стаж не надежно характеризует данную совокупность по этому признаку. 4. Из условия задачи имеем n/N=0,36, n = 100. На основе этих данных с вероятностью 0,954найдем предельную ошибку ( 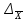 ) выборочной средней ( ) выборочной средней (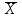 ) и возможные границы по следующим формулам ) и возможные границы по следующим формулам 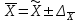 , где , где 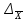 = =  ---предельная ошибка выборочной средней. Так как р=0,997 то t=3 . ---предельная ошибка выборочной средней. Так как р=0,997 то t=3 . 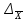 = =  года года 13,8-1,64 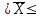 13,8+1,64 13,8+1,6412,16 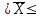 15,44 15,44  Итак, с вероятностью р=0,997 можно утверждать, что границы генеральной среднего стажа находятся от 12,16 до 15,44 лет. |
