Контрольная работа Математика. математика 2 семестр Ганюшина. Решение Для удобства оформим данные задачи в таблице. Вид продукта
 Скачать 191.25 Kb.
|
|
Контрольная работа Вариант 6 Задание 1 Для изготовления двух видов соков используются слива, черника и клубника. Общее количество сливы - 300 кг, черники - 270 кг, клубники - 400 кг. На сок 1 вида расход продуктов в частях составляет соответственно 2 : 1 : 4, на сок 2 вида - соответственно, З : З : 1. Найти оптимальный план производства двух видов соков, обеспечивающий максимальную прибыль, если цена одного кг сока 1 вида равна 25 руб., а 1 кг сока 2 вида - 45 руб. а) Записать математическую модель задачи. б) Решить задачу графическим методом. Решение: Для удобства оформим данные задачи в таблице.
Составим математическую модель задачи. 1. Введем переменные задачи: х1 – количество кг. Сока 1, планируемое к производству; x2 – количество кг. Сока 2, планируемое к производству. 2. Составим систему ограничений: 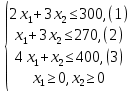 3. Зададим целевую функцию: 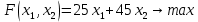 Построим область допустимых решений задачи. Для этого в прямоугольной декартовой системе координат построим прямую 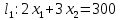 , соответствующую ограничению (1). Для этого найдем координаты двух точек, принадлежащих данной прямой. Полагаем x1=0, тогда x2 = 100, возьмем x2 = 0, получаем x1=150. Получили координаты точек В (150, 0) и С (0, 100).Определим, какая из двух полуплоскостей, на которые эта прямая делит всю координатную плоскость, является областью решений неравенства (1). Для этого подставим, например, координаты точки О(0; 0), не лежащей на прямой l1, в данное ограничение, получаем 0 ≤ 300, следовательно точка О лежит в полуплоскости решений. Укажем данную полуплоскость штриховкой (рис.1). 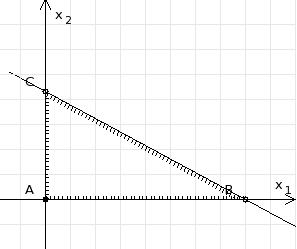 рис. 1 Аналогично строим прямую 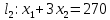 , соответствующую ограничению (2) , находим полуплоскость решений. Координаты точек пересечения с осями E(270, 0) и D(0, 90). Точку пересечения двух прямых (1) и (2) обозначим F. Отметим штриховкой общую часть полуплоскостей решений (рис. 2).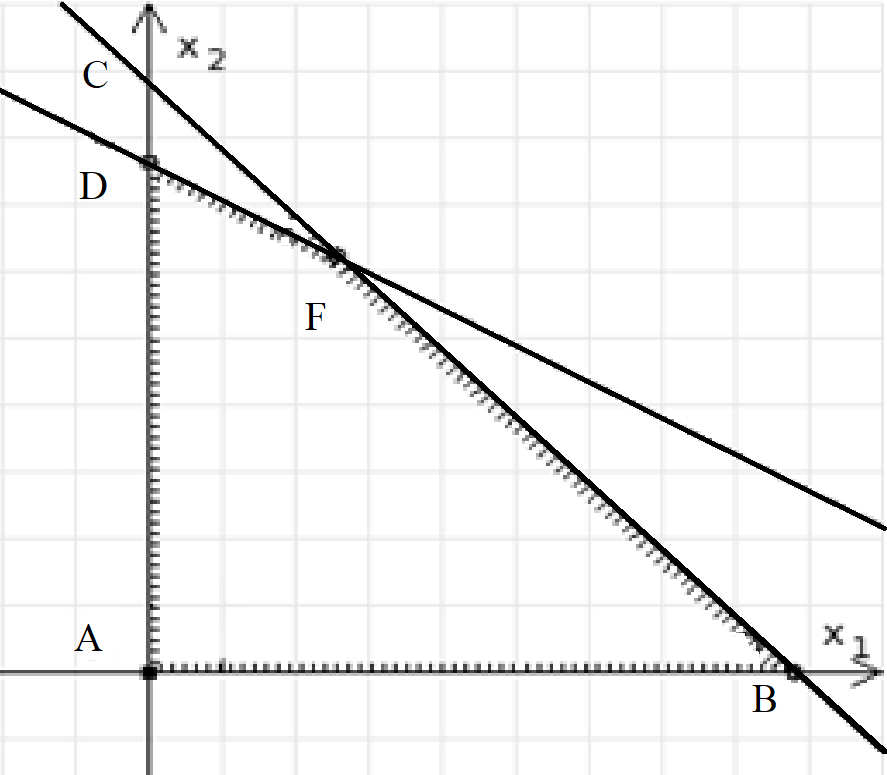 рис. 2 Строим прямую 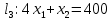 , соответствующую ограничению (3), находим полуплоскость решений. Координаты точек пересечения с осями G(100, 0) и H(0, 400). Точку пересечения двух прямых (1) и (3) обозначим I. Далее находим общую часть полуплоскостей решений, учитывая при этом условия неотрицательности переменных. Полученную область допустимых решений ADFIG отметим штриховкой (рис. 3).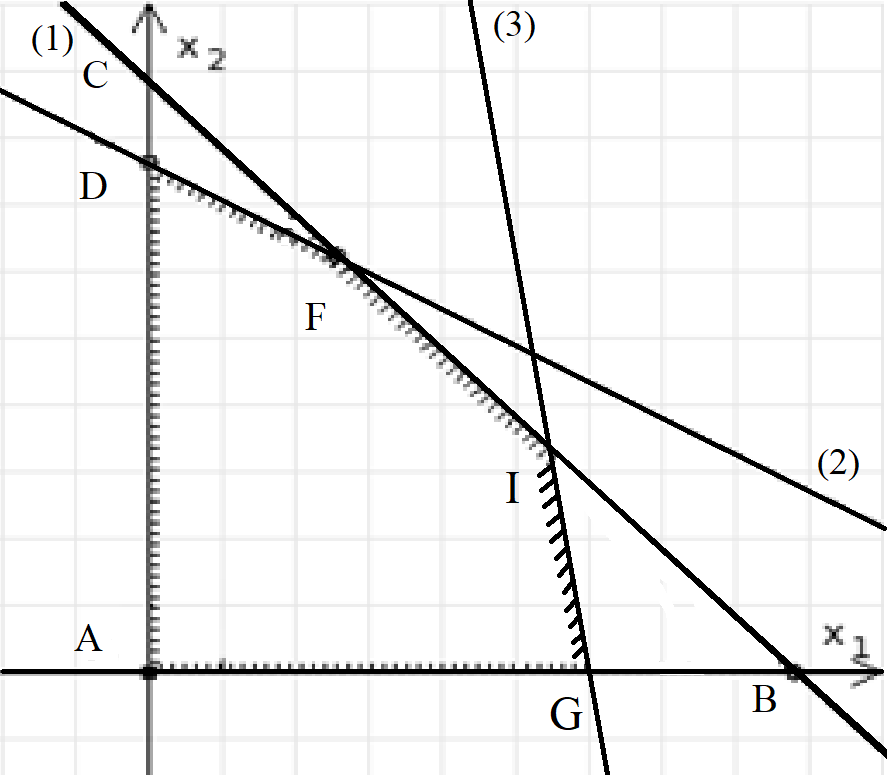 рис. 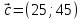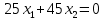3 Построим нормаль линий уровня  и одну из линий, например .Так как решается задача на нахождение максимума целевой функции, то линию уровня перемещаем в направлении нормали до последней точки многоугольника решений ADFIG (рис. 4). 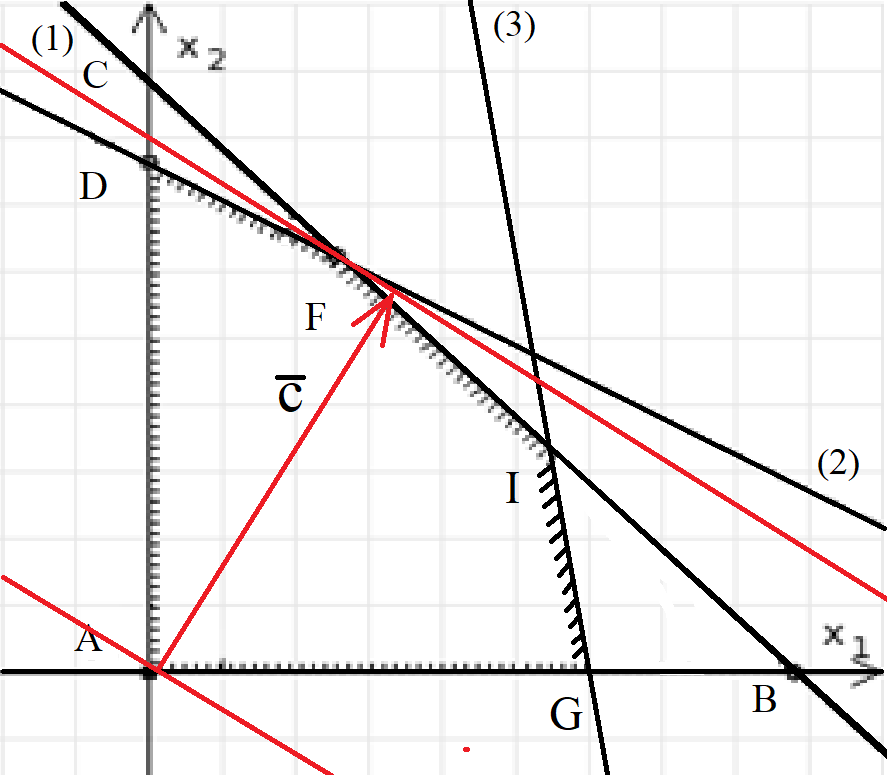 рис. 4 Видим, что последней точкой данного прямоугольника будет точка F. В данной точке значение функции будет наибольшим. Для нахождения координат точки F = l1 ∩ l1 необходимо решить систему уравнений 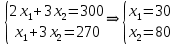 Получим координаты точки F(30, 80). Тогда находим значение целевой функции: F(30;80) = 25·30 + 45·80 = 4350. Ответ: Для получения максимальной прибыли 4350 руб., необходимо производить 30 кг Сока 1 и 80 кг. Сока 2. Задание 2 Игра проводится до выигрыша одним из двух игроков 2 партий подряд (ничьи исключаются). Вероятность выигрыша партии каждым из игроков равна 0,5. Найти вероятность того, что игра закончится раньше пятой партии Решение: Для простоты будем обозначать "1" - выиграл первый игрок и "0" - второй. Тогда ход игры можно записать в виде последовательности нолей и единиц. Например, все возможные варианты игры из двух партий: "00", "01", "10" и "11". Вероятность исхода партии p=0,5 делает равновероятными всевозможные варианты исхода последовательности партий, например, в игре из двух партий: P(00) = 0,5*0,5 = 0,25; P(01) = 0,5*0,5 = 0,25; P(10) = 0,5*0,5 = 0,25; P(11) = 0,5*0,5 = 0,25. Разделим событие H = {игра закончится до 5-ти партий} на события: Событие A = {игра закончится после 2 партий}. P(A) = P(00) + P(11) = 0,25 + 0,25 = 0,5. Событие B = {игра закончится после 3 партий}. P(B)=P(011)+P(100)=0,5*0,5*0,5+0,5*0,5*0,5=0,125+0,125=0,25. Событие C = {игра закончится после 4 партии}. P(С)=P(0100)+P(1011)=0,5*0,5*0,5*0,5+0,5*0,5*0,5*0,5=0,0625+0,0625= =0,125. Итого имеем: P(H)=P(A)+P(B)+P(С)=0,5+0,25+0,125=0,875. Ответ: P(H)=0,875. Задание 3 12 отдыхающих, среди которых 2 женщины, случайным образом разбиваются для игры в волейбол по 6 человек. Найдите вероятность того, что обе женщины попадут в одну команду. Решение: Событие А = {обе женщины в одной команде}. Общее число возможных элементарных исходов испытания равно: 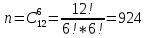 Подсчитаем число исходов, благоприятствующих интересующему нас событию (две женщины в одной команде), учтем, что таких команд возможно две: 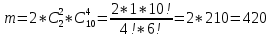 Следовательно, 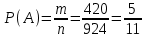 Ответ: 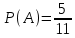 | |||||||||||||||||||||||||||