Математика. Решение Для получения уравнения изоклин положим, тогда
 Скачать 52.79 Kb. Скачать 52.79 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА
МОСКВА 2022 Задача 1. Методом изоклин построить интегральные кривые уравнения 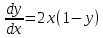 Решение Для получения уравнения изоклин положим 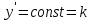 , тогда , тогда 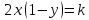 , , 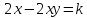 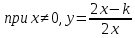 При 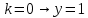 При  При 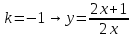 Изоклинами являются гиперболы. При k=0 получим изоклину y=1. Это прямая делит плоскость на две части. 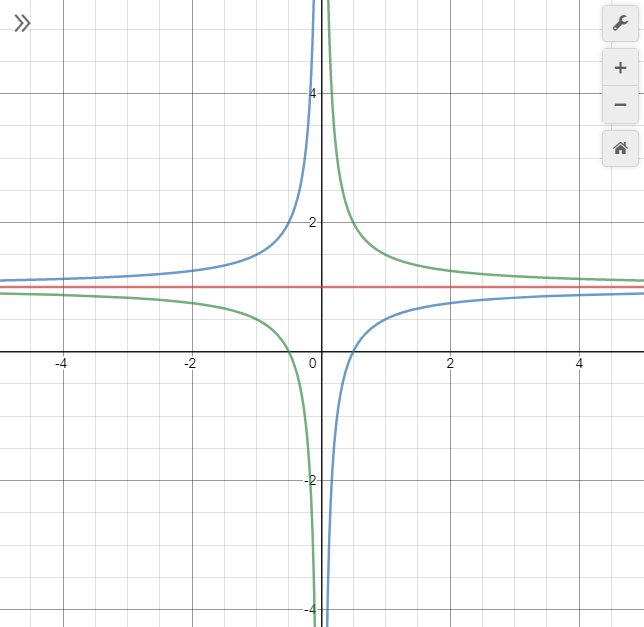 Задача 2. Решить уравнение, допускающее понижения порядка 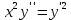 Решение Делаем замену 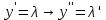 Подставляем в исходное уравнение 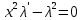 Данное уравнение является неоднородным, производим замену переменных 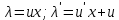 Получаем 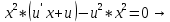 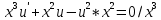 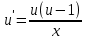 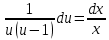 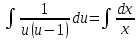 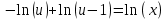 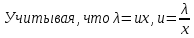 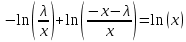 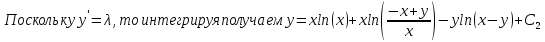 Задача 3. Решить систему уравнения 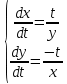 Решение Записываем систему в следующем виде 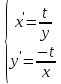 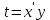 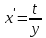 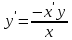 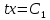 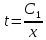 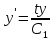 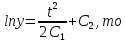 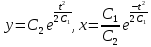 Задача 4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение Наивероятнейшее число испытания определяют из двойного неравенства: 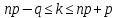 По условию 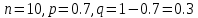 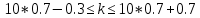 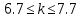 Поскольку число Поскольку число 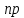 – целое, то наивероятнейшее число – целое, то наивероятнейшее число 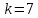 |
