Лекция+10. Решение для вертикальной сосредоточенной силы в условиях плоской задачи (рис в)

• Название: Решение для вертикальной сосредоточенной силы в условиях плоской задачи (рис в)
• Дата: 01.12.2021
• Размер: 0.77 Mb.
• Имя файла: Лекция+10.doc
• Тип: Решение; #288459

Лекция 10.

3. 3. Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности.
Распределение напряжений в основании зависит от формы фундамента в плане. В строительстве наибольшее распространение получили ленточные, прямоугольные и круглые фундаменты. Таким образом, основное практическое значение имеет расчет напряжений для случаев плоской, пространственной и осесимметричной задач.

Напряжения в основании определяется методами теории упругости. Основание при этом рассматривается как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения.

3.3.1. Задача о действии вертикальной сосредоточенной силы.

Решение задачи о действии вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства полученное в 1885 г. Ж. Буссинеском, позволяет определить все компоненты напряжений и деформаций в любой точке полупространства от действия силы (рис. 3.4.а).





Вертикальные напряжения определяются по формуле:
, где . (3.6)

Используя принцип суперпозиции можно определить значение вертикального сжимающего напряжения в точке при действии нескольких сосредоточенных сил, приложенных на поверхности (рис. 3.4.б):

(3.7)

В 1892 г. Фламан получил решение для вертикальной сосредоточенной силы в условиях плоской задачи (рис. 3.4.в):

; ; , где (3.8)

Зная закон распределения нагрузки на поверхности в пределах контура загружения, можно, интегрируя выражение (3.6) в пределах этого контура, определить значения напряжений в любой точке основания для случая осесимметричной и пространственной нагрузки (рис. 3.5.), а интегрируя выражение (3.8) – для случая плоской нагрузки.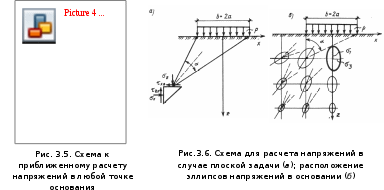




3.3.2. Плоская задача. Действие равномерно распределенной нагрузки.
Схема для расчета напряжений в основании в случае плоской задачи при действии равномерно распределенной нагрузки интенсивностью показана на рис. 3.6.а.

Точные выражения для определения компонент напряжений в любой точке упругого полупространства были получены Г. В. Колосовым в виде:

; ; , (3.9)

где , , - коэффициенты влияния, зависящие от безразмерных параметров и ; и – координатные точки, в которой определяются напряжения; – ширина полосы загружения.

На рис. 3.7. а-в показано в виде изолиний распределение нарпряжении 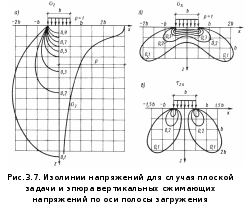, и в массиве грунте для случая плоской задачи.




В некоторых случаях при анализе напряженного состояния основания оказывается удобнее пользоваться главными напряжениями. Тогда значения главных напряжений в любой точке упругого полупространства под действием полосовой равномерно распределенной нагрузки можно определить по формулам И. Х. Митчелла:

, (3.10)

где - угол видимости, образованный лучами, выходящими из данной точки к краям загруженной полосы (рис.3.6.б).

3.3.3. Пространственная задача. Действие равномерно распределенной нагрузки.

В 1935 г. А. Лявом были получены значения вертикальных сжимающих напряжений в любой точке основания от действия нагрузки интенсивностью , равномерно распределенной по площади прямоугольника размером .

Практический интерес представляют компоненты напряжений 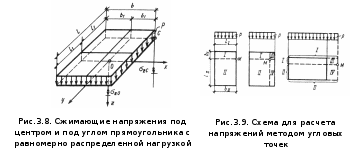, относящиеся к вертикали, проведенной через угловую точку этого прямоугольника, и , действующие по вертикали, проходящей через его центр (рис. 3.8.).



Используя коэффициенты влияния можно записать:

; , (3.11)

где - и - соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точки, в которой определяются напряжения.

Между значениями и имеется определенное соотношение.

. (3.12)

Тогда оказывается удобным выразить формулы (3.11) через общий коэффициент влияния и записать их в виде:

; . (3.13)

Коэффициент зависит от безразмерных параметров и : , (при определении углового напряжения ), (при определении напряжения под центром прямоугольника ).

3.3.4. Метод угловых точек.
Метод угловых точек позволяют определить сжимающие напряжения в основании по вертикали, проходящей через любую точку поверхности. Возможны три варианта решения (рис.3.9.).

Пусть вертикаль проходит через точку , лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения как сумму угловых напряжений I и II прямоугольников, т.е.

. (3.13)

Если точка лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда:

. (3.14)

Наконец, если точка лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой.

. (3.15)
3.3.5. Влияние формы и площади фундамента в плане.

На рис. 3.10. построены эпюры нормальных напряжений 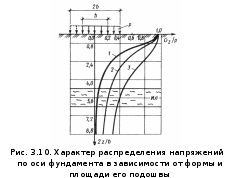по вертикальной оси, проходящей через центр квадратного фундамента при (кривая 1), ленточного фундамента (кривая 2), и тоже, шириной (кривая 3).



В случае пространственной задачи (кривая 1) напряжения с глубиной затухают значительно быстрее, чем для плоской задачи (кривая 2). Увеличение ширины, а, следовательно, и площади фундамента (кривая 3) приводит к ещё более медленному затуханию напряжений с глубиной.