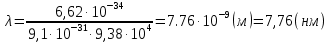Задачи. Решение Мгновенное значение тока в цепи при размыкании определяется формулой i 0
 Скачать 280.39 Kb.
|
|
3-24. Определить индукцию магнитного поля в центре контура в форме прямоугольника с диагональю 12 см. Угол между диагоналями прямоугольника равен 300. Ток в контуре 4 А. Дано: d = 12 см = 0,12 м φ = 300 I = 4 A Найти: В-? Решение  Разделим квадрат на отдельные стороны – прямые проводники с током. Магнитная индукция проводника с постоянным током в любой точке, на перпендикулярном расстоянии от него определяется:  (1)где μ0 – магнитная постоянная, r - перпендикулярное расстояние от провода до рассматриваемой точки, а θ1 - угол между линией, соединяющий верхнюю точку прямого провода с рассматриваемой точкой и перпендикуляр, опущенный на провод, а θ2, из нижней точки провода. Найдем тогда индукцию в центре по принципу суперпозиций:  Определим направление магнитной индукции по правилу правого винта, получим, что все вектора сонаправлены, значит 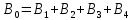 (2)Определим магнитные индукции отдельных проводников по формуле (1): 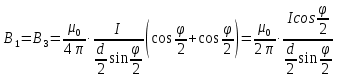 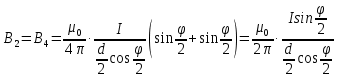 Следовательно, чтобы определить величину полной магнитной индукции в O подставим эти формулы в (2):   Проверка:  Ответ: индукция в центре прямоугольника 1,07·10-4 Тл 6-24. По замкнутой цепи с сопротивлением R = 23 Ом течет ток. Через 10 мс после размыкания цепи сила тока в ней уменьшилась в 10 раз. Определить индуктивность цепи. Дано: R = 23 Ом Δt = 10 мс = 0.01 с  Найти: L-? Решение: 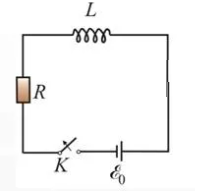 Мгновенное значение тока в цепи при размыкании определяется формулой:  I0 – начальное значение силы тока, R – сопротивление в цепи, L – ее индуктивность, Δt -время переходного процесса. Из этого уравнения выразим индуктивность:  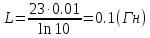 Проверка:  Ответ: индуктивность в цепи 0,1 Гн 3-26. Между полюсами электромагнита в горизонтальном магнитном поле находится проводник длинной 0,5 м, расположенный перпендикулярно линиям магнитной индукции поля. Определить ток, текущий через проводник, если он висит горизонтально, не падая. Индукция магнитного поля 0,01 Тл. Масса проводника 1 кг. Дано: l = 0,5 м В = 0,01 Тл m = 1 кг Найти: I -? Решение 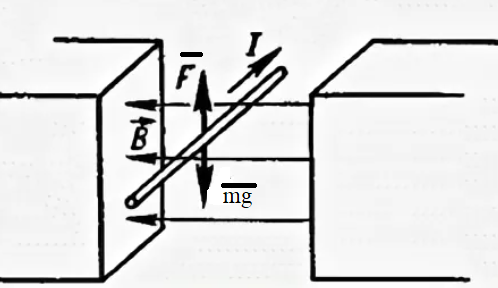 На проводник действует сила тяжести mg, направленная вниз, и сила Ампера со стороны магнитного поля FA, направленная вверх (определяем по правилу левой руки в соответствии с условием). Проводник висит, не падая, значит силы скомпенсированы. Тогда FA = mg (1) По закону Ампера: FA = IBl·sinα I – сила тока в проводнике, B-магнитная индукция, l – длина проводника, α – угол между векторами магнитной индукции и направлением тока. По условию α= 90°, тогда sinα=1. Значит FA = IBl. Подставим в (1), выразим ток: 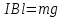   Проверка:  Ответ: сила тока в проводнике 2 мА 6-26. Источник тока замкнули на катушку с сопротивлением r = 10 Ом. По истечении времени t = 0,23 с сила тока в цепи I достигла величины равной 0,9 от предельного значения. Определить индуктивность катушки. Дано: R = 10 Ом Δt = 0,23 с  Найти: L-? Решение Мгновенное значение тока в цепи при размыкании определяется формулой: I0 – начальное значение силы тока, R – сопротивление в цепи, L – ее индуктивность, Δt -время переходного процесса. Из этого уравнения выразим индуктивность:  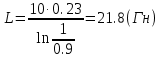Проверка: Ответ: индуктивность в цепи 21.8 Гн 1-19. На пути света поставлена стеклянная пластина толщиной d = 1 мм так, что угол падения луча равен 30°. На сколько изменится оптическая длина пути луча? Дано: d = 1 мм = 10-3 м α= 30° n1 = 1 n2 = 1.5 Найти: ΔL-? Решение 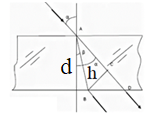 Когда луч шел в воздухе, его оптический путь L был равен его геометрическому пути L1, так как показатель преломления воздуха n1 = 1. Стеклянная пластина изменяет оптическую длину пути, которая теперь складывается из геометрической длины пути (L1–h) луча в воздухе и оптической длины пути n2h в пластинке. L2=(L1–h)+n2h = L1 + h (n2 – 1). (1) Путь, который пройдет луч в стекле, найдем, пользуясь законом преломления:  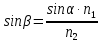  (2) Тогда из геометрических соотношений:  (3)Изменение оптической длины пути луча определяется с учетом (1): ΔL = L2 -L1= L1 + h (n2 – 1) -L1 = h (n2 – 1) Произведем вспомогательные расчеты по (2) и (3) и определим изменение оптической длины пути луча: 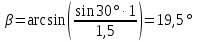 (2) Тогда из геометрических соотношений: 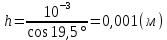 ΔL = 0,001 (1,5 – 1) = 5·10-4 (м) Ответ: изменение оптической длины пути луча 5·10-4 м 1-87. Плоскости поляризации двух призм Николя образуют между собой угол в 30°. Как изменится интенсивность света, прошедшего через эти призмы, если угол между их плоскостями поляризации станет равным 60° Дано: φ1 = 30° φ2 = 60° Найти: I1/I2-? Решение 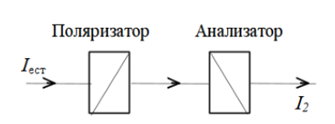 Определим интенсивность света, прошедшего анализатор по закону Малюса: I1 = I0·cos2φ1 I2 = I0·cos2φ2 I0 – интенсивность естественного света, φ – угол между плоскостями поляризации. Определим, как изменится интенсивность света: 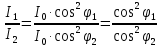 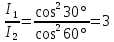 Ответ: интенсивность света уменьшится в 3 раза 1-57. Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол φ = 30°. На какой угол отклоняет она спектр четвертого порядка? Дано: n1 = 3 φ3 = 30° n2 = 4 Найти: φ4 -? Решение  Воспользуемся условием дифракционных максимумов для решетки: d·sinφ = nλ, где d – порядок решетки, φ – угол дифракции, n – порядок максимума, λ – длина волны падающего света. Применим эту формулу для двух случаев, определим угол дифракции для четвертого порядка: d·sinφ3 = n3λ (1) d·sinφ4 = n4λ (2) Из (1): 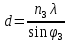 Подставим в (2): 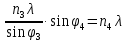 Отсюда  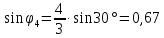  Ответ: решетка отклоняет спектр четвертого порядка на 42° 1-95. Естественный свет падает на кристалл каменной соли с показателем преломления 1,544. Определить коэффициент отражения при нормальном падении лучей. Дано: n1 = 1 n2 = 1.544 Найти: k-? Решение  В случае нормального падения естественного света на плоскую границу раздела сред коэффициент отражения вычисляется по формуле: 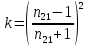 n21 = n2/n1 – относительный показатель преломления второй среды относительно первой.  Ответ: коэффициент отражения 0,046 2-37. Максимальная энергия фотоэлектронов при освещении металла светом с частотой 2,2×1015 Гц оказалась в два раза больше, чем при освещении светом с частотой 4,6×1015 Гц. Найдите работу выхода электрона из металла. Дано: Wmax1=2 Wmax2 ν1 = 2,2·1015 Гц ν2 = 4,6·1015 Гц Найти: А-? Решение Используем уравнение Эйнштейна для фотоэффекта определим энергию падающего света: 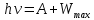 ,где h-постоянная Планка, ν-частота падающего света, А -работа выхода, Wmax – максимальная энергия фотоэлектронов Для обоих случаев:  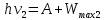 Выразим максимальную энергию фотоэлектронов, поделим оба равенства друг на друга, выразим работу выхода:      Ответ: работа выхода 0,83 эВ 2-52. С какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны 520 нм? Дано: λ = 520 нм =520·10-9 м Найти: v-? Решение Энергия фотона, заданная через длину волны падающего света λ: 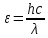 h – постоянная Планка, c – скорость света в вакууме. Из определения кинетической энергии:  m – масса электрона находим  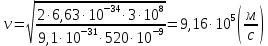 Проверка:  Ответ: скорость электрона 9,16·105 м/с 2-35. Красная граница фотоэффекта для рубидия равна 810 нм. Какова максимальная энергия (в эВ) фотоэлектронов, испускаемых рубидием под действием ультрафиолетовых лучей с длиной волны 100 нм? Дано: λкр = 810 нм = 810·10-9 м λ = 100 нм = 100·10-9 м Найти: Wmax-? Решение Зная красную границу фотоэффекта, по уравнению Эйнштейна для красной границы определим работу выхода для металла:  (1)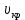 - красная граница – минимальная частота, при которой начинается фотоэффект. Она связана с длиной волны соотношением λкр: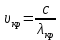 (2)Подставим (2) в (1):  (3)Используем уравнение Эйнштейна для фотоэффекта определим энергию фотоэлектронов: 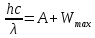 ,где h-постоянная Планка, ν-частота падающего света, А -работа выхода, Wmax – максимальная энергия фотоэлектронов    Произведем проверку:  Ответ: энергия фотоэлектронов 10,9 эВ 2-95. Найдите длину волны де Бройля нейтрона с энергией 0,025 эВ Дано: W = 0,025 эВ Найти: λ-? Решение
|
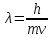
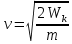
<< c, следовательно,