Прикладная. Прикладная механика Ямщиков. Горизонтальноковочная машина

• Название: Горизонтальноковочная машина
• Анкор: Прикладная
• Дата: 12.05.2023
• Размер: 396.5 Kb.
• Имя файла: Прикладная механика Ямщиков.doc
• Тип: Пояснительная записка; #1125067

ФЕДЕРАЛЬНОЕ АГЕНСТВО РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Механика»

Расчетно-пояснительная записка

к расчётно-графической работе по

теории машин и механизмов

на тему

« Горизонтально-ковочная машина»
Задание 2 вариант 2

Выполнил: студент гр. 1-ФММТ-106, Ямщиков Д.В..

Руководитель: Горелов В.Н.
Самара 2023 г.

Содержание.

Расчетно-пояснительная записка 1

к расчётно-графической работе по 1

теории машин и механизмов 1

Содержание. 2

Задание 3

Введение. 4

1.Структурный анализ механизма. 4

2.1. Кинематический синтез кривошипно-ползунного механизма. 6

2.2. План положений. 7

2.3. План скоростей и ускорений. 8

2.3.1. План скоростей. 8

2.3.2. План ускорений. 10

2.4. Кинематические диаграммы. 12

3. Силовой расчет. 14

3.1. Обработка индикаторной диаграммы. 14

3.2. Силовой расчёт группы Ассура второго класса. 14

3.2.1.Определение сил инерции. 15

3.2.2.Определение сил тяжести. 16

3.2.3. Определение реакций в кинематических парах. 16

3.3 Силовой расчёт механизма I класса. 17

3.3.1 Определение силы тяжести. 18

3.3.2 Определение реакций в кинематических парах. 18

3.4 Рычаг Жуковского. 19

Список литературы. 20

Задание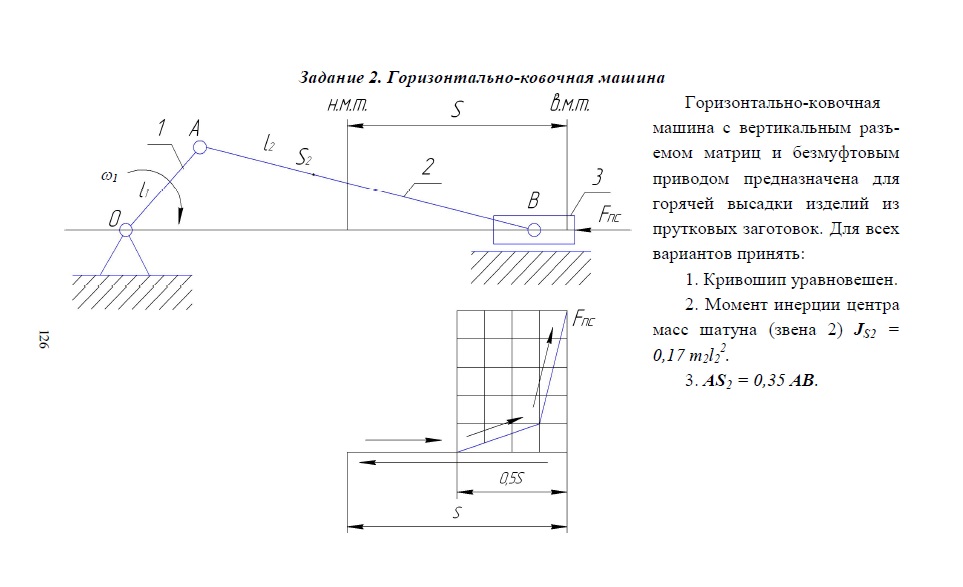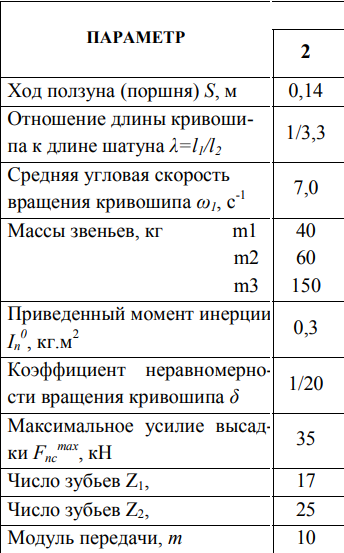

Введение.

Целью данной курсовой работы является проектирование и исследование механизма горизонтально-ковочная машина.

1.Структурный анализ механизма.

Кривошипно-ползунный механизм состоит из четырех звеньев:

0 – стойка,

1 – кривошип,

2 – шатун,

3 – ползун.

Также имеются четыре кинематические пары:

I – стойка 0-кривошип OA

II – кривошип OA-шатун AB

III – шатун AB-ползун B

IV – ползун B-стойка 0.

I, II и III являются вращательными парами

IV – поступательная пара.

Все кинематические пары являются низшими, т.е. p_нп=4, p_вп=0.

Степень подвижности механизма определяется по формуле Чебышева:

W3n2p_нпp_вп, (0)

где n – число подвижных звеньев, n = 3

P_нп – число низших пар,

P_вп – число высших пар.

W 3*3-2*4 1.

По классификации И.И. Артоболевского данный механизм состоит из механизма I класса стойка 0-кривошип OA и структурной группы II класса второго порядка шатун AB-ползун B. Из этого следует, что механизм является механизмом II класса.
2. Кинематический анализ.

2.1. Кинематический синтез кривошипно-ползунного механизма.

Первоочередной задачей проектирования кривошипно-ползунного механизма является его синтез, т. е. определение размеров звеньев по некоторым первоначально заданным параметрам.

• 
  Ход ползуна S=0,14 м.
  
• 
  Эксцентриситет e=0, т.е. опоры механизма находятся на одном уровне.
  
• 
  Угловая скорость карданного вала  
  
• 
  Передаточное отношение цепной передачи U_n
  
• 
  Число зубьев колес Z₁Z₃=17; 25
  

Длину кривошипа l₁ определяем из рассмотрения двух крайних положений механизма, определяющих ход ползуна S

SOB₁OB₂l₁l₂l₂l₁2l₁, (2)

Откуда

l₁S2, (3)

l₁0,1420,07 м.

Длина шатуна:

l₂l₁, (4)

l₂4*3.30,213 м

Расстояние от точки А до центра масс S₂ шатуна

l₃0,35l₂, (5)

l₃0,350,23108085м

Угловая скорость кривошипа  

  ₁7 c^-1  6

2.2. План положений.

План положений  это графическое изображение механизма в n последовательных положениях в пределах одного цикла.

План положений строим в двенадцати положениях, равностоящих по углу поворота кривошипа. Причем все положения нумеруем в направлении вращения кривошипа  . Положения остальных звеньев находим путем засечек. За нулевое начальное положение принимаем крайнее положение, при котором ползун наиболее удален от кривошипного вала начало работы хода. Начальное положение кривошипа задается углом ₀, отсчитанным от положительного направления горизонтальной оси кривошипного вала против часовой стрелки. Для данного механизма ₀0рад. Кривая, последовательно соединяющая центры S , S , S …S масс шатуна в различных его положениях, будет траекторией точки S₂.

Выбираем масштабный коэффициент длин _l:

μ_l(l₁₊l₂)/300мм (7)

где l₁ − действительная длина кривошипа, м l₂ − действительная длина кривошипа, м

μ_l0,07+0,231/3000,001 ммм.

Отрезок AB, изображающий длину шатуна l₂на плане положений, будет:

ABl₂_l, (0)

AB0,2310,001231мм.

Расстояние от точки А до центра масс S₂ шатуна на плане положений:

AS₂l₃_l, (0)

AS₂0,080850,00180,85мм.

Вычерчиваем индикаторную диаграмму с таким же масштабом перемещения _s0,001ммм, в каком представлен план положений механизма, для которой выбираем масштабный коэффициент давления

_pF_псL_p, (0)

где F_псмаксимальная нагрузка, Н.

L_pизображающий его отрезок на индикаторной диаграмме, мм.

_p3500087,5360Нмм.

Кинематическую схему механизма вычерчиваем на листе 1 в указанном масштабном коэффициенте _l0,005ммм.

2.3. План скоростей и ускорений.

План скоростей – это графическое изображение в виде пучка лучей абсолютных скоростей и точек звеньев и отрезков, соединяющих концы лучей, представляющих собой отношение скорости точек в данном положении механизма.

Определение плана ускорений аналогично определению плана скоростей.

Планы скоростей и ускорений будем рассматривать для десятого положения.

2.3.1. План скоростей.

Скорость точки А находим по формуле:

V_A₁l₁, (0)

где ₁ – угловая скорость кривошипа, с^-1.

l₁ – длина кривошипа, м.

V_A70,070,49мс

Выбираем масштабный коэффициент плана скоростей _V:

_VV_APa, (0)

где V_Aскорость точки A, мс

Paизображающий ее отрезок на плане скоростей, мм.

_V0.49490,01.

Из полюса P в направлении вращения кривошипа перпендикулярно к OA откладываем отрезок Pa, изображающий вектор скорости точки A, длиной 49мм.

Определяем скорость точки В:

_B _A _BA, (0)

где _BA- вектор скорости точки B в ее вращательном движении относительно точки A, перпендикулярно к оси звена AB.

Из точки а на плане скоростей перпендикулярно оси звена AB проводим прямую до пересечения с линией действия скорости точки B, в результате чего получаем отрезок Pb41,27мм, изображающий вектор скорости точки B и отрезок ab26,42мм, изображающий вектор скорости звена AB.

Тогда

V_BPb_V, (0)

V_B41,270,010,4127мc

V_BAab_V, (0)

V_BA26,420,010,2642мс.

Скорость точки S₂ находим из условия подобия:

as₂abAS₂AB, (0)

Откуда

as₂AS₂ABab, (0)

as₂26,429,247мм.

Соединив точку S₂ с полюсом P, найдем отрезок, изображающий вектор скорости точки S₂, т.е. Ps₂44,7мм.

Тогда

V_S2Ps₂_V, (0)

V_S244,70,010,447мс.

Если из произвольной точки отложить вектор V_S2 для всех двенадцати положений и соединить их конечные точки плавной кривой, то получим годограф скорости точки S₂.

По результатам расчета программы ТММ1 строим годограф скорости точки S₂.

Угловую скорость шатуна AB определяем по формуле:

₂V_BAl₂, (0)

₂0,26420,2131,24 c^-1.

2.3.2. План ускорений.

Находим нормальное ускорение точки A:

a_A l₁, (0)

a_A7²0,073,43мс².

Выбираем масштабный коэффициент плана ускорений _a:

_aa_APa, (0)

где a_A – нормальное ускорение точки A,мс²

Pa – изображающий ее отрезок на плане ускорений, мм.

_a3,4350686мс²мм.

Из полюса P откладываем отрезок Pa, изображающий вектор нормального ускорения точки A кривошипа, который направлен к центру вращения кривошипа.

Определяем ускорение точки B:

, (0)

где  вектор ускорения точки B в ее вращательном движении относительно точки A.

Определяем ускорение a :

a V l₂, (0)

a 0,2642²0,2130,3277мc².

Из точки a на плане ускорений проводим прямую, параллельную оси звена AB и откладываем на ней параллельно отрезку AB в направлении от точки B к точке A отрезок an, представляющий собой ускорение a в масштабе _a.

ana _a, (0)

an0,32770,06864,777мc²мм.

Из точки n проводим прямую перпендикулярную оси звена AB до пересечения с линией действия ускорения точки B, в результате чего получаем отрезок nb35,15мм, изображающий вектор касательного ускорения звена AB и отрезок Pb32,49мм, изображающий вектор скорости точки B.

Тогда

a nb_a, (0)

a 35,150,06862,4113мс²

a_B Pb_a, (0)

a_B32,490,06862,223мc².

Соединив точки a и b, получим отрезок ab85мм, изображающий вектор ускорения звена AB.

Тогда

a_BAab_a, (0)

a_BA35,360,06862,4257мс².

Ускорение точки S₂ находим из условия подобия:

as₂abAS₂AB, (0)

Откуда

as₂AS₂ABab, (0)

as₂35,3612,376мм.

Соединив точку s₂ с полюсом P, найдем отрезок, изображающий вектор скорости точки S₂, т.е. Ps₂41,35мм.

Тогда

a_S2Ps₂_a, (0)

a_S241,350,06862,83661 мс².

Если из произвольной точки отложить вектор a_S2 для всех двенадцати положений и соединить их конечные точки плавной кривой, то получим годограф ускорения точки S₂.

По результатам расчета программы ТММ1 строим годограф ускорения точки S₂.

Угловое ускорение шатуна AB определяем по формуле:

₂ a l₂, (0)

₂2,41130,21311,321 c^-2.

2.4. Кинематические диаграммы.

Строим диаграмму перемещений S_BS_B на основе восьми положений ползуна B₀, B₁, B₂, …,B₈ и соответствующих положений кривошипа A₀, A₁, A₂, …, A₈.

Находим масштабные коэффициенты:

○ длины: _S=k·_l _S=0,5·0,001=0,0005 ммм.

○ угла поворота  кривошипа: _2 L, _=2·3,14160=0,03925 радмм.

○ времени: _t2 ₁L, _t=2·3,147·160=0,00561 смм.

Строим диаграмму скорости V_BV_B методом графического дифференцирования диаграммы S_BS_B. Полюсное расстояние H₁35 мм. Тогда масштабный коэффициент скорости  определим по формуле:

_V_S₁_ H₁, (0)

_V0,00270,03925350,0102мсмм.

Продифференцировав диаграмму V_BV_B, получим диаграмму a_Ba_B. Полюсное расстояние H₂35 мм. Масштабный коэффициент ускорения определим по формуле:

_a_V₁_ H₂, (0)

_a0,010270,03925350,05197мс²мм.

Относительная погрешность вычислений:

Таблица №

Метод расчета	Параметр	Значение в положении 7	Значение по результам расчета программы ТММ1	Относительная погрешность , %
Метод планов	VB, м/с	0,4127	-	-
	VS2, м/с	0,447	-	-
	2, с-1	1,24	-	-
	aB, м/с2	2,223	-	-
	aS2, м/с2	2,83661	-	-
	2, с-2	11,321	-	-
Метод диаграмм	VB, м/с	0,231	-	-
	aB, м/с2	2,33	-	-

3. Силовой расчет.

Основной задачей силового расчета является определение реакций в кинематических парах механизма и внешней уравновешивающей силы уравновешивающего момента, являющейся реактивной нагрузкой со стороны отсоединенной части машинного агрегата.

В основу силового расчета положен принцип Даламбера, позволяющий при приложении к звеньям инерционной нагрузки записать уравнения движения в форме уравнений равновесия. При этом рассматриваются статически определимые кинематические цепи группы Ассура и механизм I класса, т.е. звено кривошипа.

3.1. Обработка индикаторной диаграммы.

Индикаторная диаграмма самоходной тележки представляет собой зависимость движущих сил от перемещения ползуна PfS .

Для определения значения движущих сил для всех рассматриваемых положений механизма, необходимо произвести графическую обработку индикаторной диаграммы. Давление P_i МПа на поршень в i-том положении определим путем измерения соответствующей ординаты y в мм на диаграмме с учетом масштабного коэффициента давлений _p, подсчитанного в п. 2.2.

P_i_py_i. (0)

Движущая сила, действующая на поршень F_дi, Н будет равна:

F_дi P_iD²4, (0)

где D – диаметр поршня, м.

3.2. Силовой расчёт группы Ассура второго класса.

Для выполнения силового расчёта необходимо знать значение сил, действу- ющих на звенья механизма: силы тяжести, движущие силы и силы инерции этих звеньев.

Силовой расчёт будем вести для десятого положения кривошипно-ползунного механизма.

От механизма, начиная с исполнительного звена ползуна, отсоединяется группа Ассура, а точки разрыва этой группы заменяются реакциями.

3.2.1.Определение сил инерции.

Модули сил инерции звеньев определяем по формуле:

Ф_im_ia_i , (0)

где m_i-масса i-го звена, кг

a_i-ускорение центра масс i-го звена, мс² .

Подставив числовые значения, получим:

Ф₂60·2,83661170,1966Н

Ф₃1502,223333,45Н

Направления сил инерции противоположны направлениям соответствующих ускорений. Момент инерции шатуна определяется по формуле:

M_Ф2I_S2₂ (0)

M_Ф20,39219,194,44Нм

Систему сил инерции шатуна, т.е. главный вектор сил инерции Ф₂, приложенный в центре масс, и момент сил инерции относительно центра масс, приводим к одной силе Ф₂ приложенной в некоторой точке K. Расстояние между линиями действия силы инерции и приведенной силой вычисляется по формуле:

hM_Ф2Ф₂ (0)

h4,44170,19660,02609 м

Направление приведенной силы совпадает с направлением силы инерции, а направление момента приведенной силы относительно точки S₂ совпадает с направлением момента M_Ф2 Рисунок 2.

3.2.2.Определение сил тяжести.

Силы тяжести определяем по формуле:

G_im_ig , (0)

где m_iмасса i-го звена, gускорение силы тяжести.

Подставив числовые значения, получим:

G₂609,81588,6Н

G₃1509,811471,5Н.

3.2.3. Определение реакций в кинематических парах.

Определение давлений в кинематических парах начинаем с рассмотрения равновесия группы Ассура 2-3 Рисунок 3: шатун AB – ползун B. На звенья этой группы действуют силы: движущая сила F_д, силы тяжести G₃, G₂, результирующие силы инерции Ф₃, Ф₂, реакция R₀₃ заменяющая действие стойки 0 на ползун 3 и реакция R₁₂ заменяющая действие кривошипа 1 на шатун 2.

Силы, приложенные в точке B, приводим к одной силе F₃.Величину этой силы определяем по формуле:

F₃Fпс+Ф₃+G₃ (0)

F₃₌6300+1471,5+333,458104,95Н

Знак  показывает, что сила F₃ направлена вверх.

Условие равновесия группы 2-3 выражается следующим образом:

    0 (0)

Давление R₁₂ раскладываем на две составляющие, действующие вдоль оси звена AB – R и перпендикулярно к оси звена AB – R .

Составляющую R определяем из уравнения моментов всех сил, действующих на шатун AB, относительно точки B.

Применительно к рисунку 3 это уравнение можно записать так:

R ABФ₂h₁-G₂h₂0 (0)

откуда

R Ф₂h₁G₂h₂AB (0)

R  170,1966108,37588,6146,66231453,542 Н.

План сил строим в масштабе: _F=81,0495 Нмм.

Из произвольной точки последовательно откладываем вектора R , F₃G₂,Ф₂. Через конечную точку вектора Ф₂ проводим линию действия реакции R₀₃ ,а через начальную точку вектора R линию действия силы R . Получим точку пересечения. Соединив конечную точку вектора Ф₂ с точкой пересечения, получим вектор R₀₃. Соединив точку пересечения с конечной точкой вектора R , получим вектор R₁₂.Умножив соответствующие длины на масштабный коэффициент, получим R₀₃2116,20245 H R₁₂8264,61754 H R 8252,46011 Н

Давление R₃₂ в паре шатун – ползун определяем из условия равновесия ползуна:

  0 (0)

и равенства:

R₃₂-R₂₃, (0)

или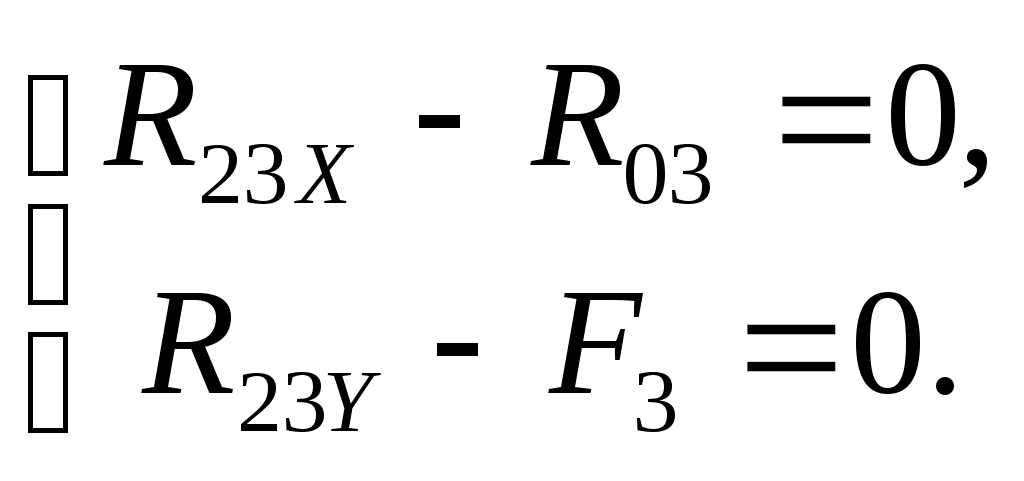

(0)

Тогда

R_23XR₀₃2116,20245 H,

R_23YF₃8104,95H

R₂₃ (0)

R₃₂8376,66564 Н.

3.3 Силовой расчёт механизма I класса.

К кривошипу приложена сила тяжести G₁, известная реакция R₂₁R_12. Неизвестная по значению и направлению реакция R₀₁ показана в виде R и R .

Чтобы кривошип мог совершать вращение по заданному закону, к нему со стороны отсоединённой части машинного агрегата должна быть приложена реактивная нагрузка в виде уравновешивающей силы F_y. Допустим, что неизвестная по модулю уравновешивающая сила приложена перпендикулярно кривошипу в точке А.

Силу инерции кривошипа не определяем, так как он уравновешен.

3.3.1 Определение силы тяжести.

Силу тяжести кривошипа определяем по формуле:

G₁m₁g, (0)

где m₁ – масса кривошипа

g – ускорение силы тяжести.

G₁409,81392,4Н

3.3.2 Определение реакций в кинематических парах.

Давление R₀₁ в паре кривошип-стойка и уравновешивающий момент M_y определяем из условия равновесия кривошипа ОА:

0 (0)

Силу F_y находим из условия:

-F_y OA +R₂₁h₃0 (0)

Откуда

F_yR₂₁h₃OA (0)

F_y8264,6175461,37707245,7083Н

План сил строим в масштабе: _F=81,0495 Нмм.

В соответствии с уравнением из произвольной точки последовательно откладываем вектора F_y, R₂₁, G₁. Соединив конечную точку вектора G₁ с начальной точкой вектора F_y получим вектор R₀₁.Отложив параллельно OA из конца вектора G₁ прямую до пресечения с линией действия вектора F_y, получим вектор R . Соединив конечную точку вектора R с начальной точкой вектора F_y, получим вектор R . Умножив соответствующие длины на масштабный коэффициент, получим: R₀₁8662,57Н.

Уравновешивающий момент M_yопределяется по формуле:

M_yF_yl₁ (0)

M_y7245,70830,07=507,2 Нм

3.4 Рычаг Жуковского.

С целью проверки правильности силового расчета механизма уравновешивающий момент M_y определяем с помощью рычага Жуковского.

На план скоростей предварительно повёрнутый на 90 градусов вокруг полюса в соответствующие точки переносим все заданные силы, включая силы инерции и уравновешиващую силу. Из условия равновесия плана скоростей, как рычага, определяем уравновешивающую силу F_y последнюю прикладываем в точке a, считая ее как бы приложенной в точке A кривошипа, и направляем ее перпендикулярно линии кривошипа ОА.

Таким образом:

F_yPaФ_ph₄G₂h₅F₃Pb0 (0)

Откуда:

F_yФ_ph₄G₂h₅F PbPa (0)

F 170,196613,19 588,646,02 8104,9541,27 497424,97045Н

Определяем величину уравновешивающего момента:

M F l , (0)

M 7424,970450,00751975Нм

Относительная погрешность вычислений:

Таблица №

Метод расчета	Параметр	Значение в положении №8	Значение по результам расчета программы ТММ1	Относительная погрешность , %
Метод планов	R12, Н	8264,61754	-	-
	R03, Н	2116,20245	-	-
	R01, Н	8662,57	-	-
	My, Нм	507,2	-	-
Рычага Жуковского	My, Нм	519,75	-	-

Список литературы.

1. 
   Теория механизмов и машин. Учебник для вузов / Под редакцией К.В. Фролова. М.: Высшая школа,1987.
   
2. 
   Курсовое проектирование по теории механизмов и машин / Под ред. А.С. Кореняко 5-е издание. Киев: Вища школа,1970.
   
3. 
   Кинематическое и динамическое исследование кривошипно-ползунных механизмов с применением ЭВМ в диалоговом режиме: Методические указания к курсовому проекту по теории механизмов машин /Самарский Политехнический Институт; Сост. А.С. Неймарк, А.К. Федосеев, Самара, 1991.
   
4. 
   Проектирование зубчатых механизмов с применением ЭВМ в диалоговом режиме: Методические указания к курсовому проекту по теории механизмов машин / Самарский Государственный Технический Университет; Сост. А. С. Неймарк, И. Н. Булавинцев, Самара, 1993.
   
5. 
   Синтез кулачковых механизмов с применением ЭВМ в диалоговом режиме: Методические указания к курсовому проекту по теории механизмов и машин/ Самарский Государственный Технический Университет; Составители: А.С. Неймарк, Э.Э. Рыжов, И.Н. Булавинцев. Самара 1993.