график. 1_ЛР Графики + Транс. Лабораторная работа 1 Создание графиков
 Скачать 1.8 Mb.
|
|
Лабораторная работа №1 «Создание графиков» Построение графиков является частным случаем построения диаграмм. Графики выбирают в тех случаях, когда хотят отобразить изменение данных за равные промежутки времени, ведь по графику удобно проследить не только величину изменения, но и в первую очередь, скорость изменения величины. Для графиков существует возможность соединить точки плавной линией. Задание 1. На отрезке [-1;1] вычислите значение функции с шагом 0,2. 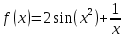 Решение: Создайте таблицу данных. 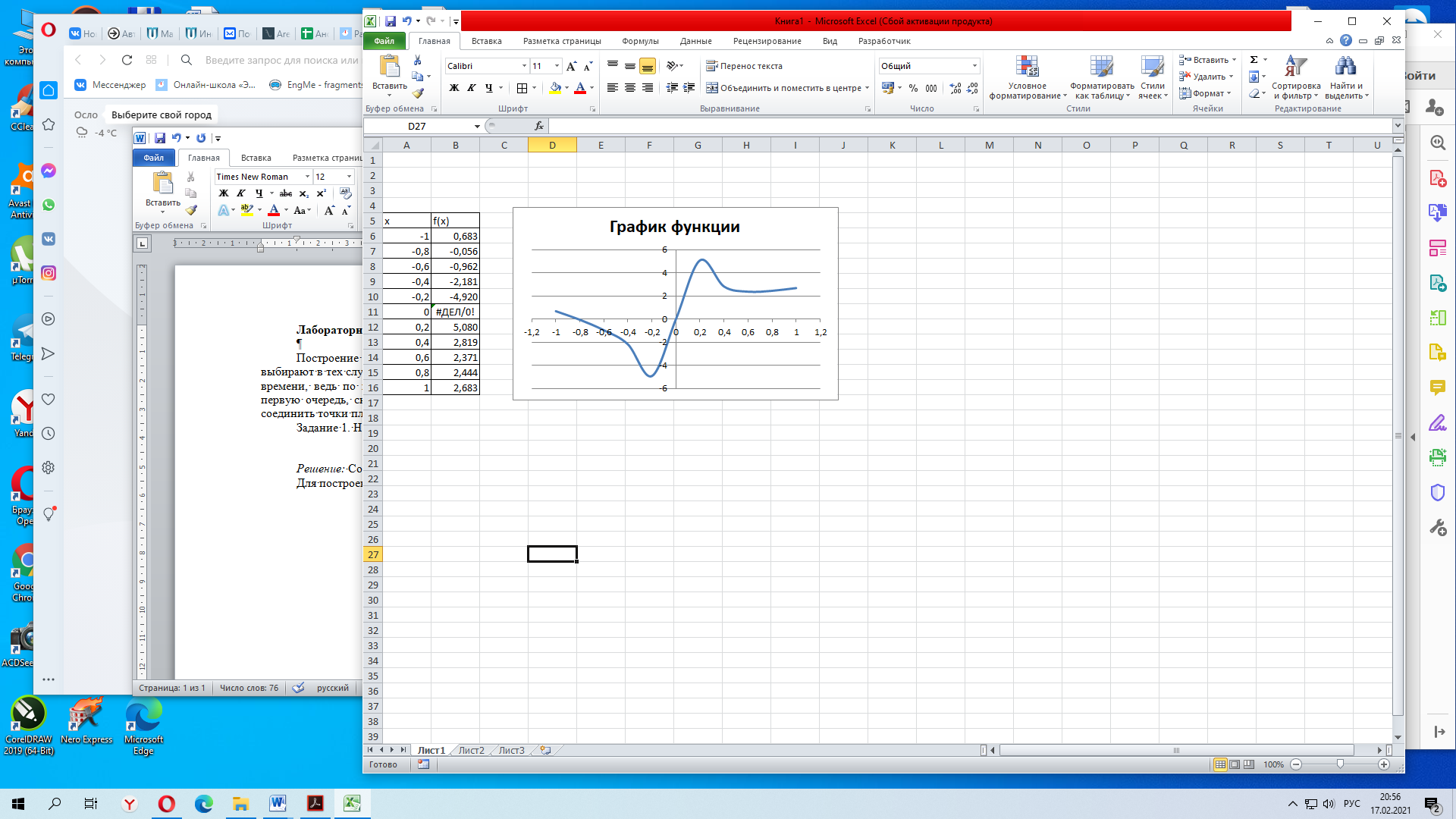 По полученным значениям, постройте график функции в виде точечной диаграммы. Примечание: Для построения графика выделите таблицу данных (столбец А и В). Задание 2. Построение двух графиков в одной системе координат. Построить в одной системе координат графики следующих двух функций: y = 2sin(x) и z = 3cos(2x) – sin(x) при x [-3; 3] В ячейки A2:A17 вводите значения переменной x от –3 до 3 с шагом 0,2. В ячейки B1 и C1 вводите y и z соответственно, а в ячейки B2 и C2 – формулы: = 2*sin(A2) =3*cos(2*A2) – sin(A2) В 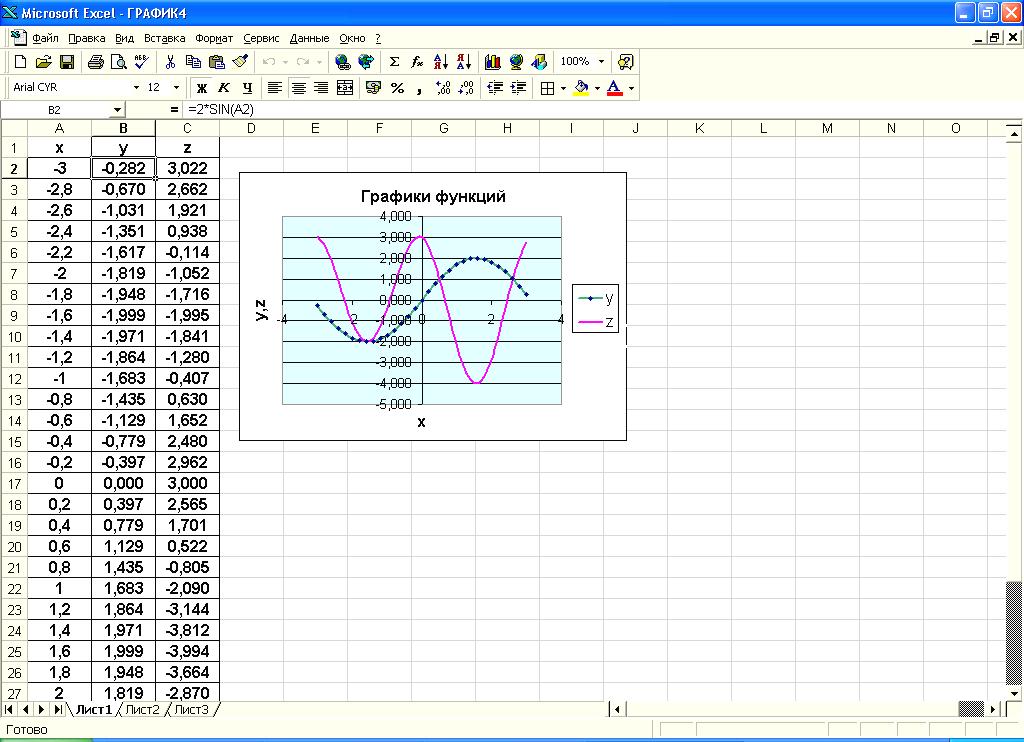 ыделите диапазон ячеек A1:C32 и постройте график функции в виде точечной диаграммы. Рисунок – Фрагмент листа Excel Самостоятельно постройте график функции для аргумента, изменяющегося с данным шагом в определенном интервале по вариантам: Используйте для расчета функции EXP(x) – ex, LN(x) – lnx, |x| – ABS(x) , КОРЕНЬ(х) = (x)^(1/2) - 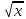 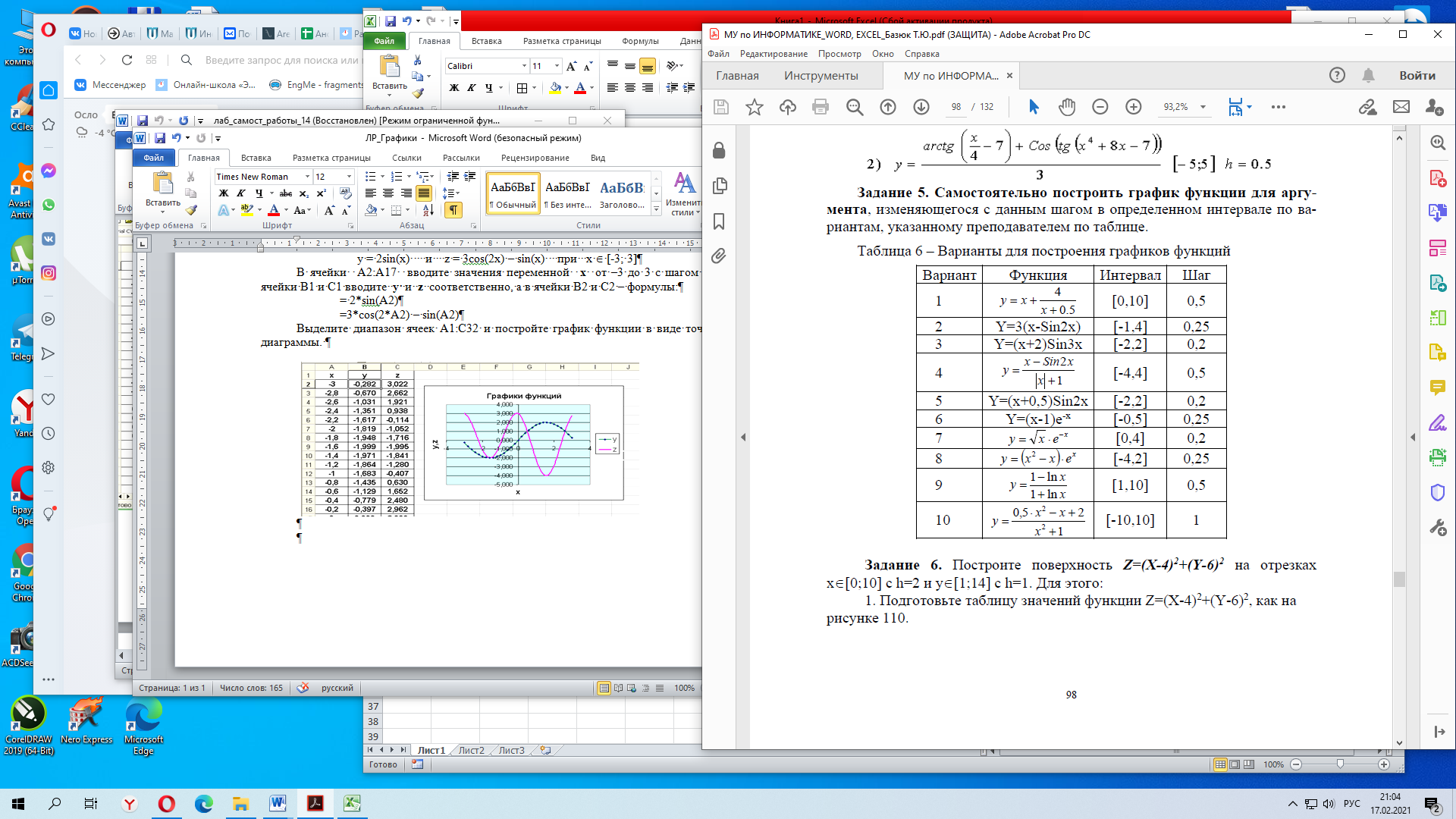 Задание 3. Построение алгебраических и трансцендентных линий на плоскости Часто различные линии на плоскости задаются в полярных координатах, общее уравнение которых можно записать в виде: 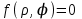 , где ρ,φ – полярные координаты. Если линия задана уравнением 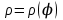 в полярных координатах, то ее уравнение в декартовых координатах можно записать в виде: 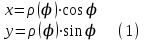 Итак, зная уравнение линии в полярных координатах, легко построить график в декартовой системе координат. Для этого следует: 1. Подготовить диапазон изменения координаты φ. 2. Рассчитать значение функции на данном диапазоне в полярных координатах 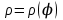. 3. Рассчитать значения х и у в декартовой системе координат по формулам (1). 4. Выделить диапазон области определения и области значения функции, т.е. все значения х и у на рабочем листе, и построить график. Для построения графиков лучше использовать типы диаграмм Точечная. 5. Отформатировать полученный график. Учитывая приведенные рекомендации, легко построить также и линии на плоскости, заданные параметрически (см задание 4). Построить функцию, заданную уравнением в полярных координатах: 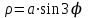 , а = 6, φ [0, 4] с шагом 0,05, в ячейку G2 введите число 6.Разместите на листе книги Excel заголовки четырех столбцов: φ, р, х, у, как показано на рисунке. Ввести формулы для расчета. В ячейку В2 – формулу в виде =$G$2*SIN(3*А2), в ячейку D2 – в виде =В2*CОS(А2), в ячейку Е2 – в виде =В2*SIN(А2). Автозаполнением заполните столбцы B, D, E 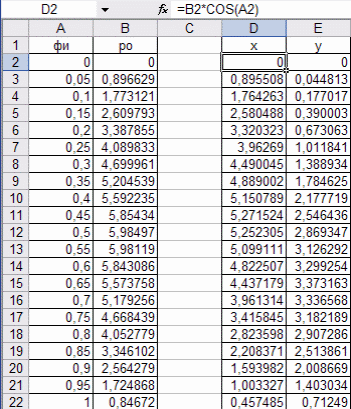 Постройте график функции используя тип диаграммы Точечная. Проверьте, как изменяется вид функции при варьировании константы а. 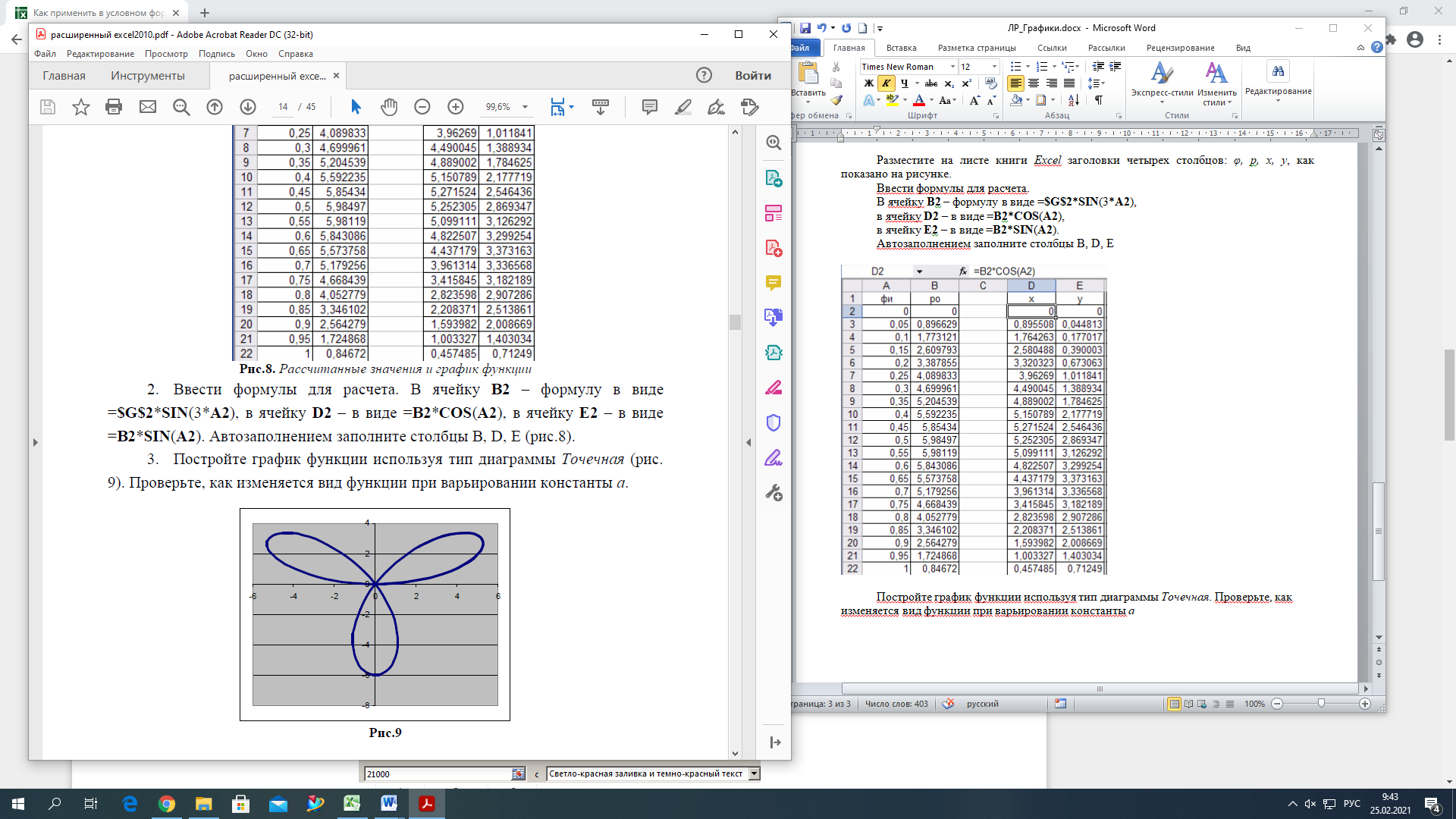 Самостоятельная работа Используя возможности Excel, постройте функцию, заданную уравнением. 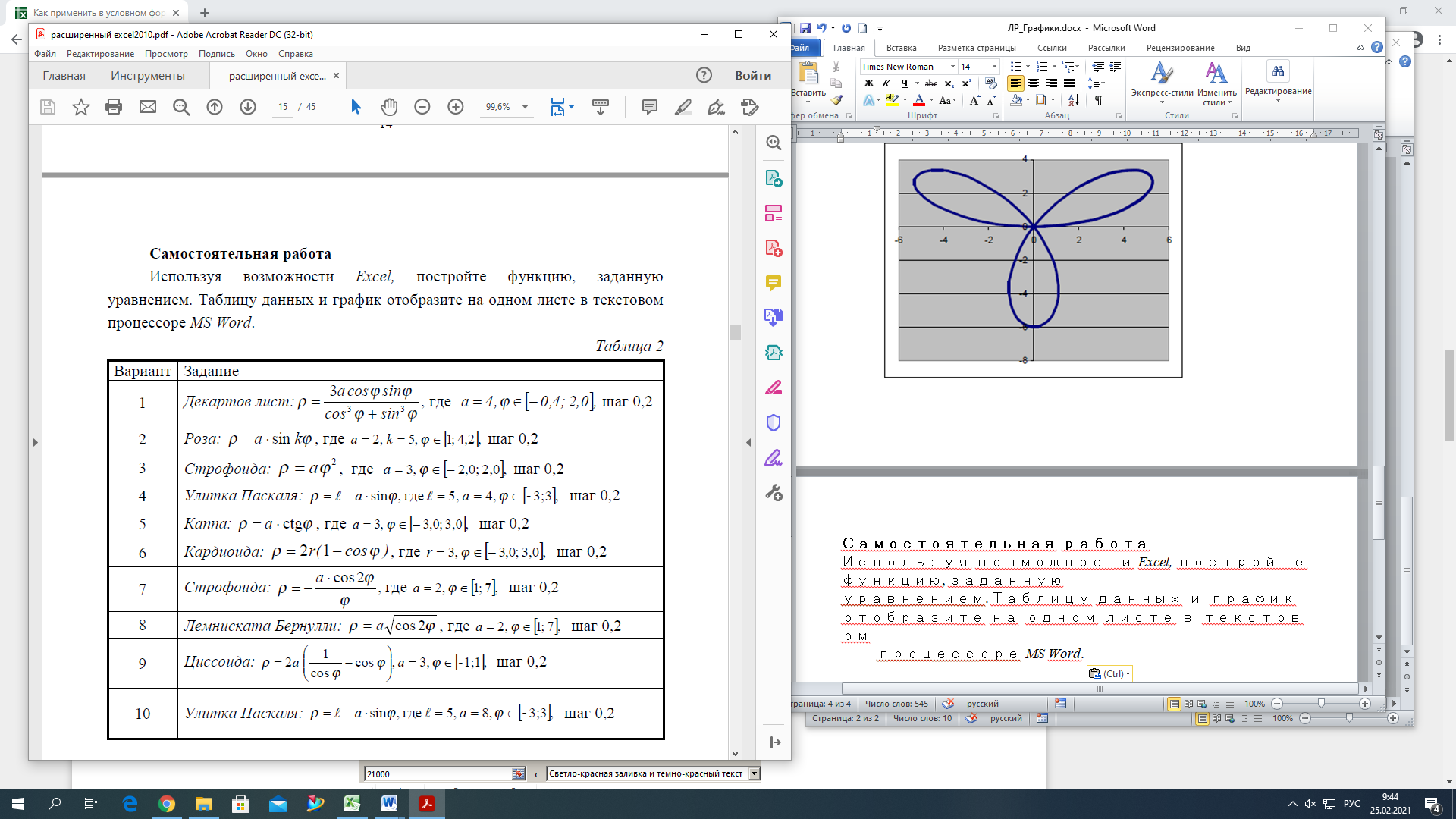 Задание 4. Построения графика параметрически заданной функции. 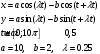 в ячейку G2 введите число 10, в G3 – число 2, в G4 – число 0,25. Разместите на листе книги Excel заголовки трех столбцов: t, х(t), у(t), как показано на рисунке. Параметр t задан от 0 до 10 π (это примерно до 31,5), введите данные автозаполнением или через кнопку Заполнить / Прогрессия, укажите начальное и конечное значение, предварительно выделив произвольный диапазон (примерно 62 ячейки). 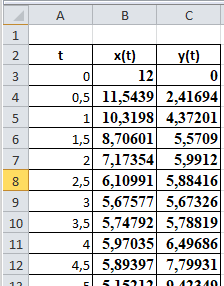 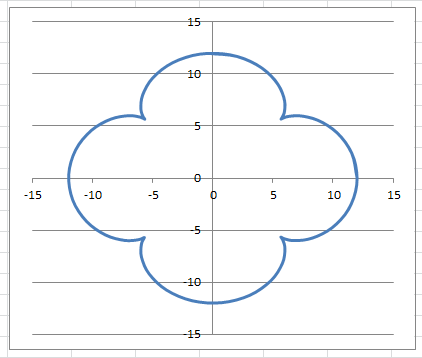 Введите формулы для расчета. В ячейку В3 – формулу в виде =G2*COS(G4 *А3)+ G3*СOS(A3+ G4* А3), в ячейку C3 формулу для расчета переменной у. Расставьте абсолютные ссылки, где необходимо, автозаполнением заполните столбцы B, C. По значениям переменных x и y необходимо построить график. Иногда, переменная t может быть задана в градусах, для ее перевода создается дополнительный столбец с формулой перевода градусов в радианы, а именно t(рад)=ГРАДУСЫ*ПИ()/180. Самостоятельно постройте спираль описанную формулой 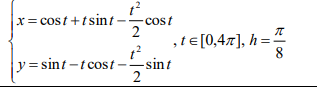 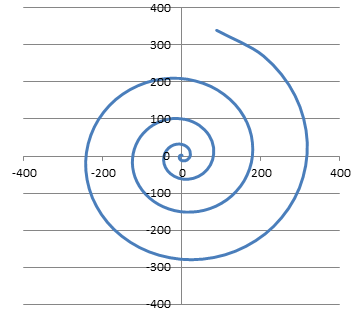 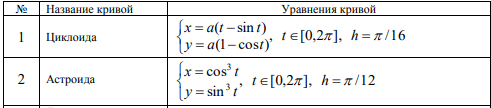   |