Оке. Лекция 7-8. ИДУ. Вычисление площадей плоских фигур, ограниченных кривыми, заданными в декартовых координатах, параметрически и в полярных координатах
 Скачать 163.68 Kb. Скачать 163.68 Kb.
|
Лекции 7 – 8.Вычисление площадей плоских фигур, ограниченных кривыми, заданными в декартовых координатах, параметрически и в полярных координатах.Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения.Вычисление длины дуги кривой и площади поверхности вращения.Вычисление площадей плоских фигур в декартовых и полярных координатах.В  Рис. 1 ычисление площадей плоских фигур в декартовых координатах  непрерывна на непрерывна на 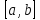 Найдем площадь фигуры, ограниченной линиями 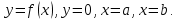 Пусть  – разбиение отрезка – разбиение отрезка 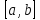 на элементарные отрезки на элементарные отрезки 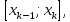 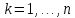 ; ;  ; ;  . .Рассмотрим площадь 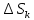 части фигуры, удовлетворяющей условию части фигуры, удовлетворяющей условию . .Пусть 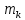 и и  – соответственно наименьшее и наибольшее значения функции – соответственно наименьшее и наибольшее значения функции  на на   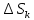 заключена между площадями прямоугольников с высотой заключена между площадями прямоугольников с высотой 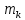 и и    Сложим по  от от  до до  : : Т.е.  где  – интегральные суммы, соответствующие разбиению – интегральные суммы, соответствующие разбиению  и выбору точек и выбору точек 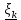 и и 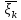 соответственно (нижняя и верхняя интегральные суммы Дарбу); при соответственно (нижняя и верхняя интегральные суммы Дарбу); при   Из (1) получаем:  Замечания:  (см. рис. 19.) (см. рис. 19.) Рис. 2 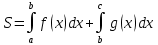 (см. рис. 20). (см. рис. 20).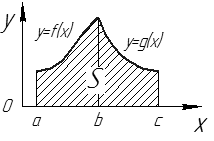 Рис. 3  (см. рис. 21). (см. рис. 21). Рис. 4 Вычисление площадей плоских фигур в полярных координатах. Рассмотрим кривую,  , где функция , где функция 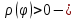 непрерывна на непрерывна на  . . Рис. 5 Найдем площадь фигуры, ограниченной линиями 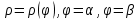 . Пусть . Пусть  – разбиение – разбиение  : : , , Рассмотрим площадь 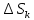 части фигуры, удовлетворяющей условию: части фигуры, удовлетворяющей условию: (см. рис. 22). (см. рис. 22).Пусть  и и  – соответственно наименьшее и наибольшее значения функции – соответственно наименьшее и наибольшее значения функции  : : . . заключена между площадями круговых секторов радиусов заключена между площадями круговых секторов радиусов 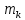 и и  : :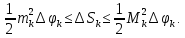 Сложим по  от от  до до  : : Т.е.  где  – интегральные суммы функции – интегральные суммы функции  , соответствующие разбиению , соответствующие разбиению  и выбору точек и выбору точек 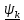 и и 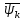 соответственно (нижняя и верхняя интегральные суммы). соответственно (нижняя и верхняя интегральные суммы). При  из (1.9.2) получаем: из (1.9.2) получаем: . .Замечания:  (см. рис. 23). (см. рис. 23). Рис. 6  (см. рис. 24). (см. рис. 24).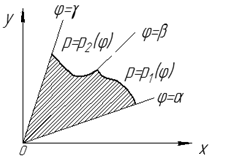 Рис. 7 Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения. Рис. 8 Рассмотрим в пространстве тело  , каждая точка , каждая точка  которого удовлетворяет неравенству которого удовлетворяет неравенству . .Пусть площадь сечения 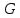 плоскостью плоскостью  равна равна   непрерывна на непрерывна на  . . Найдем объем  тела тела 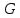 . . Зафиксируем 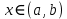 . Рассмотрим малое . Рассмотрим малое  . . Рассмотрим часть (слой) тела 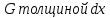 , соответствующий отрезку , соответствующий отрезку  . . Объем этой малой части  приблизительно (c точностью до бесконечно малых выше первого порядка относительно приблизительно (c точностью до бесконечно малых выше первого порядка относительно  равен объему цилиндра с площадью основания равен объему цилиндра с площадью основания  и высотой и высотой   Суммируя по всем таким тонким слоям, получаем 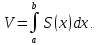 Объемы тел вращения.  Рис. 9 Фигура, ограниченная линиями  , вращается вокруг оси , вращается вокруг оси  (см. рис. 26). (см. рис. 26).Найдем объем  тела вращения. Зафиксируем тела вращения. Зафиксируем  . . Сечение тела плоскостью  – круг радиуса – круг радиуса   . . Тогда  Ту же фигуру вращаем вокруг оси  (см. рис. 27). (см. рис. 27). Рис. 10 Рассмотрим малый отрезок  , где , где 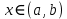 . . При вращении соответствующей части фигуры получаем тело объема  , ,где  – площадь кольца радиусов – площадь кольца радиусов  и и  соответственно: соответственно: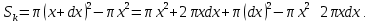 Тогда  Суммируя по тонким "слоям", получим:  Общий случай: 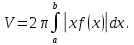 Таким образом получаем для вращения фигуры, ограниченной линиями  , имеем: , имеем: 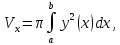  При вращении фигуры, ограниченной линиями  (см. рис. 28). (см. рис. 28).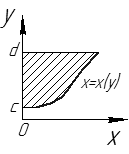 Рис. 11   Вычисление длин дуг кривых и площадей поверхностей вращенияДлина дуги кривой. Пусть дуга  задана параметрическими уравнениями: задана параметрическими уравнениями: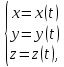  Функции  имеют на имеют на  непрерывные производные. непрерывные производные. , ,  Рассмотрим переменную точку   – переменная дуга длиной – переменная дуга длиной 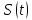 . .Дифференциал дуги   – длина всей дуги. – длина всей дуги. Случай плоской кривой:   Случай графика функции  : : Случай кривой, заданной в полярных координатах:   Площадь поверхности вращения.  Рис. 12 Рассмотрим функцию 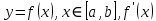 – непрерывна на – непрерывна на  Пусть  – дуга графика – дуга графика  – вращается вокруг оси – вращается вокруг оси  . . Рассмотрим ломаную 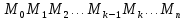 , вписанную в дугу , вписанную в дугу  , где , где (см. рис. 29). (см. рис. 29).При вращении вокруг  звена ломаной звена ломаной 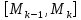 получим боковую поверхность усеченного конуса. получим боковую поверхность усеченного конуса.Опр. Площадью поверхности вращения называется предел сумм площадей боковых поверхностей усеченных конусов, полученных при вращении вписанной ломаной, при стремлении к 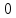 максимальной длины звена ломаной. максимальной длины звена ломаной.Площадь боковой поверхности усеченного конуса с радиусами оснований  и и 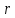 , образующей , образующей  равна: равна:  В данном случае   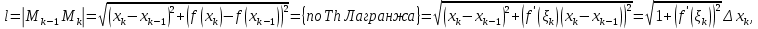  , ,  Тогда площадь боковой поверхности усеченного конуса , полученной при вращении звена ломаной   Отсюда площадь поверхности вращения равна:  или  (при  надо брать надо брать  ). ).Случай кривой, заданной параметрическими уравнениями:   Случай кривой, заданной в полярных координатах:  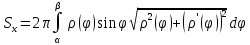 Аналогично при вращении вокруг оси  : :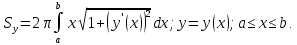 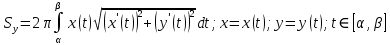 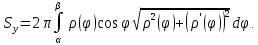 Случай произвольной оси вращения:  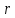 – расстояние от переменной точки кривой до оси вращения; – расстояние от переменной точки кривой до оси вращения;  – дифференциал дуги. – дифференциал дуги. |
