Эпюр №3. Взаимное пересечение кривых поверхностей. Развертки кривых поверхностей
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Министерство общего и профессионального образования Российской Федерации КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА Кафедра начертательной геометрии и машиностроительного черчения Халдеев И.М. Панин В.К. Щербаков А.В. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ. РАЗВЕРТКИ КРИВЫХ ПОВЕРХНОСТЕЙ (Расчётно-графическая работа №3) Учебно-методическое пособие. для студентов 1-го курса всех специальностей ИАНТЭ Казань 2003 УДК 514.18/077/ Составители: Халдеев И.М. Панин В.К. Щербаков А.В. Взаимное пересечение кривых поверхностей. Развертки кривых поверхностей: Учебно-методическое пособие. (эпюр№3) для студентов 1-го курса всех специальностей ИАНТЭ / Каз.гос.техн.ун-т; ; Сост. И.М. Халдеев, В.К. Панин, А.В. Щербаков. Казань, 2003. 26 с. Рассматриваются этапы выполнения эпюра № 3: решение задачи на пересечение двух кривых поверхностей, способы их решения на примерах аналогичных задач, примеры построения разверток, указания по оформлению эпюра. Табл. 1. Ил. 14. Библиогр.: 4 назв. Рецензент СОДЕРЖАНИЕ ВВЕДЕНИЕ………………………………………………………………………………… СОДЕРЖАНИЕ ЗАДАНИЯ И ПОРЯДОК ЕГО ВЫПОЛНЕНИЯ…………………………..1. Способы построения очерков кривых поверхностей.
1 1i-2i // P-Q .2. Построение гиперболы по ее вершинам А и А1 и точке М….... 1.3 Построение параболы по ее вершине A, точке M и оси I……… 1.4. Построение очерков поверхностей вращения, оси которых параллельны одной из плоскостей проекций………. 1.5. Проецирование линии пересечения двух поверхностей вращения второго порядка на плоскость, параллельную их общей плоскости симметрии………………………………………………. 1.6. Проецирование линии пересечения поверхности второго порядка с поверхностью тора на плоскость, параллельную их общей плоскости симметрии………………………… 2. Краткие сведения о способах построения линий взаимного пересечения двух кривых поверхностей…………………. 2.1. Способ вспомогательных секущих плоскостей……………….. 2. 2.Способ вспомогательных секущих концентрических сфер…. 2.3. Способ вспомогательных секущих эксцентрических сфер…. 3. Развертки кривых поверхностей……………………………………….. 3.1. Построение развертки прямого, кругового усеченного цилиндра вращения…………………………………………… СПИСОК ЛИТЕРАТУРЫ………………………………………………….. При выполнении проектных и конструкторских работ часто приходится строить линии пересечения кривых поверхностей. В авиационной и автомобильной промышленности, а также в общем машиностроении и приборостроении чаще всего используются кривые поверхности второго порядка, из элементов которых образуют проектируемые поверхности изделий сложных форм. Изготовление технологической оснастки, раскрой листовых материалов для обшивки поверхностей сложных форм, выполнение теоретических чертежей этих изделий требуют навыков в построении плоских сечений сложных поверхностей, умения строить развертки. Цель методического указания - помочь студентам в решении задач, связанных с выполнением комплексного задания "Взаимное пересечение поверхностей. Развертки поверхностей", а именно: 1. Указать основные способы решения задач на взаимное пересечение двух поверхностей при различном их расположении и сочетании. 2. Показать основные приемы построения разверток кривых поверхностей и нанесения на них найденной линии пересечения. 3. Дать рекомендации о порядке выполнения этого задания. СОДЕРЖАНИЕ ЗАДАНИЯ И ПОРЯДОК ЕГО ВЫПОЛНЕНИЯ1. Построить в трех проекциях линию взаимного пересечения поверхностей двух тел /на чертеже должны быть сохранены в тонких линиях все построения искомых точек этой /этих/ линий. /1-й формат - позиционная задача/. 2. Построить развертку одной из заданных поверхностей /цилиндр или конус/ с указанием на развертке найденной линии пересечения. Перенос точек на развертку поверхности выполнить с помощью образующих развертываемой поверхности /2-й формат - метрическая задача/. Оба формата АЗ/420 Задание для каждого студента группы индивидуальное. Оно содержит изображение двух заданных тел, которые могут быть представлены как в двух проекциях комплексного чертежа, так и в одной фронтальной проекции. Если задание дано в двух проекциях, его масштаб 1:2, и при вычерчивании на формате заданных тел в трех проекциях их размеры нужно увеличить в два раза, а в случае задания одной проекцией, следует считать, что заданные тела являются, главным образом, поверхностями вращения, имеющими общую плоскость симметрии, параллельную фронтальной плоскости проекций. Данное изображение следует ориентировать на эпюре согласно номеру на бланке задания, расположенному в верхнем правом углу. По заданной фронтальной проекции, таким образом, находят две другие проекции заданных тел - горизонтальную и профильную. Некоторые из заданных тел могут быть ограничены плоскими срезами /"основаниями"/ и представляют собой главным образом поверхности второго и четвертого порядка, то есть это могут быть цилиндры и конусы вращения: с плоскими срезами - основаниями, поверхности параболоидов вращения и гиперболоидов вращения, ограниченные аналогичными плоскими срезами, а также сферы и эллипсоиды. Кроме того: одной из заданных поверхностей может быть тор или его часть, ограниченная одним или несколькими срезами. В общем случае на задании двух тел одной фронтальной проекцией этих тел, как уже было сказано, представлены два тела с общей плоскостью симметрии, параллельной плоскости чертежа. Работу следует начать с выделения на листе бумаги формата будущего эпюра, как и при выполнении предыдущих работ, выделив в нем место основной надписи. Основные проекции размещаются на поле эпюра не скученно, а свободно, с соблюдением проекционных связей. Оси проекций на эпюре можно не наносить, а вести измерения от осей, изображенных на чертеже тел /рис.1/. 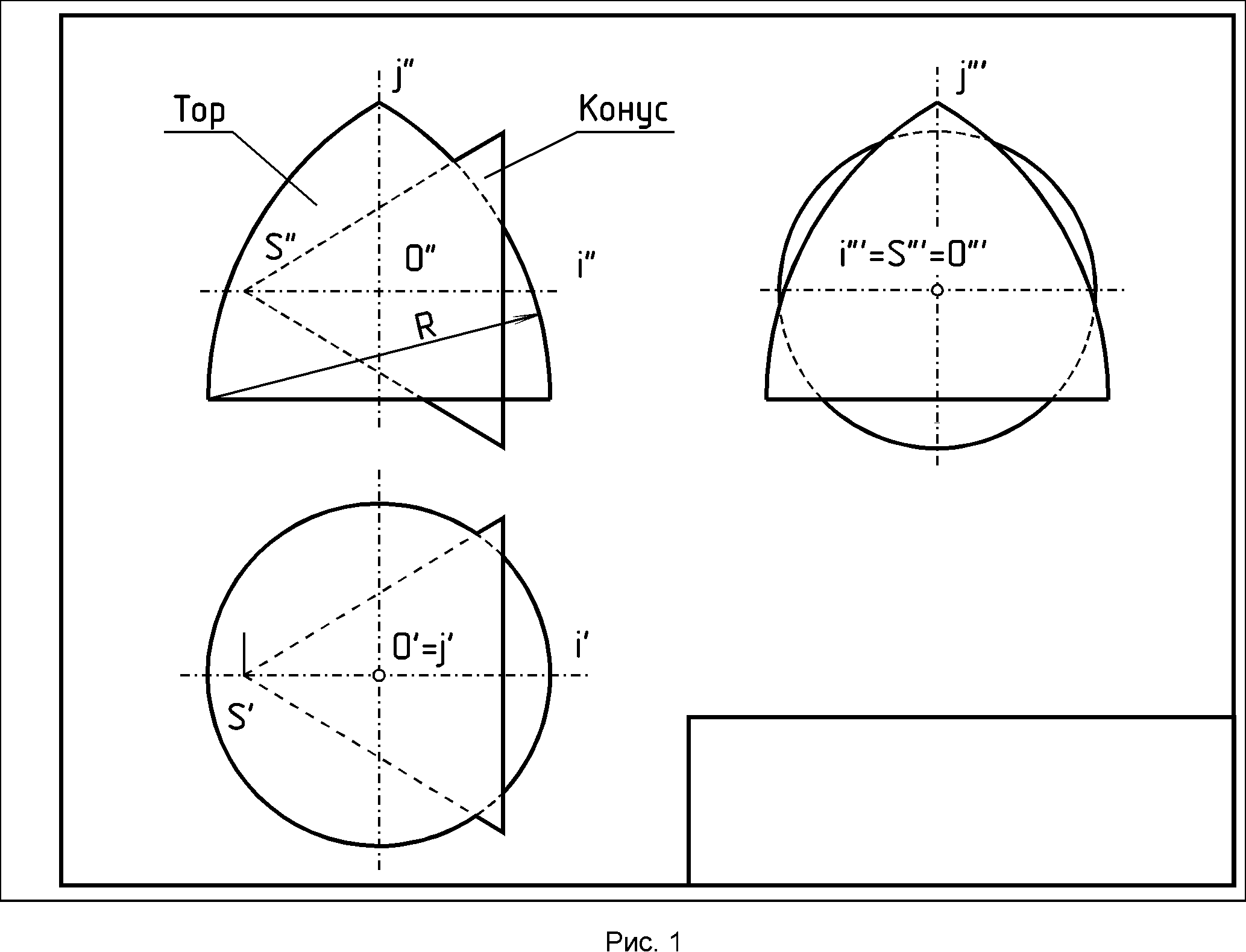 Рис.1 После изображения на чертеже в тонких линиях двух заданных тел, приступают к нахождению линии пересечения их поверхностей одним из возможных способов решения. Сначала определяют характерные или опорные точки искомой линии пересечения на всех трех проекциях заданных тел (крайние точки искомой линии, точки ее касания очерков поверхностей, а также точки изломов при переходе линии пересечения с одной поверхности на другую и т.д.), которые следует отметить на чертеже буквами или цифрами шрифтом № 5 или № 7 ГОСТ 2.304-81. Затем находят необходимое и достаточное количество промежуточных точек искомой линии пересечения кривых поверхностей друг с другом и линий пересечения этих поверхностей плоскостями оснований заданных поверхностей. Расстояния между вспомогательными секущими плоскостями или вспомогательными секущими сферами, используемыми в качестве посредников при решении эпюра, следует выбирать через 10 - 15 мм как минимум. Этого вполне достаточно для точного решения задачи нахождения линии взаимного пересечения поверхностей. Некоторые из промежуточных точек также следует обозначить буквами или цифрами. Одну из вспомогательных секущих плоскостей или вспомогательных секущих сфер следует выделить цветной линией и обозначить найденные с их помощью точки на всех трех проекциях. Все построения, выполненные в тонких линиях, сохраняются на чертеже, и после его обводки. Обводке подлежат очерковые линии и линии пересечения поверхностей, заданных тел. Рекомендуемая толщина линий обводки в пределах 0,8 - 0,9 мм, то есть равная расстоянию между штрихами масштабной линейки с ценой деления 1 мм. Рекомендуется во избежание грубых ошибок, перед обводкой эпюра, показать его преподавателю, ведущему практическое занятие в группе /получения его подписи в графе "Проверил"/. Законченная работа предъявляется преподавателю для окончательной сдачи /получения его подписи в графе "Утвердил"/. РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ОТДЕЛЬНЫХ ЭЛЕМЕНТОВ ЗАДАНИЯ 1. Способы построения очерков кривых поверхностей. Заданные на чертеже кривые поверхности являются главным образом поверхностями второго порядка. Их очерками /проекциями видимых контуров/ являются кривые второго порядка: эллипс, гипербола или парабола, а также окружности и прямые линии. Для точного построения очерков этих поверхностей нужно с задания перенести на эпюр характерные точки очерков заданных тел: вершины, точки на основаниях фигур и т.п.
Р 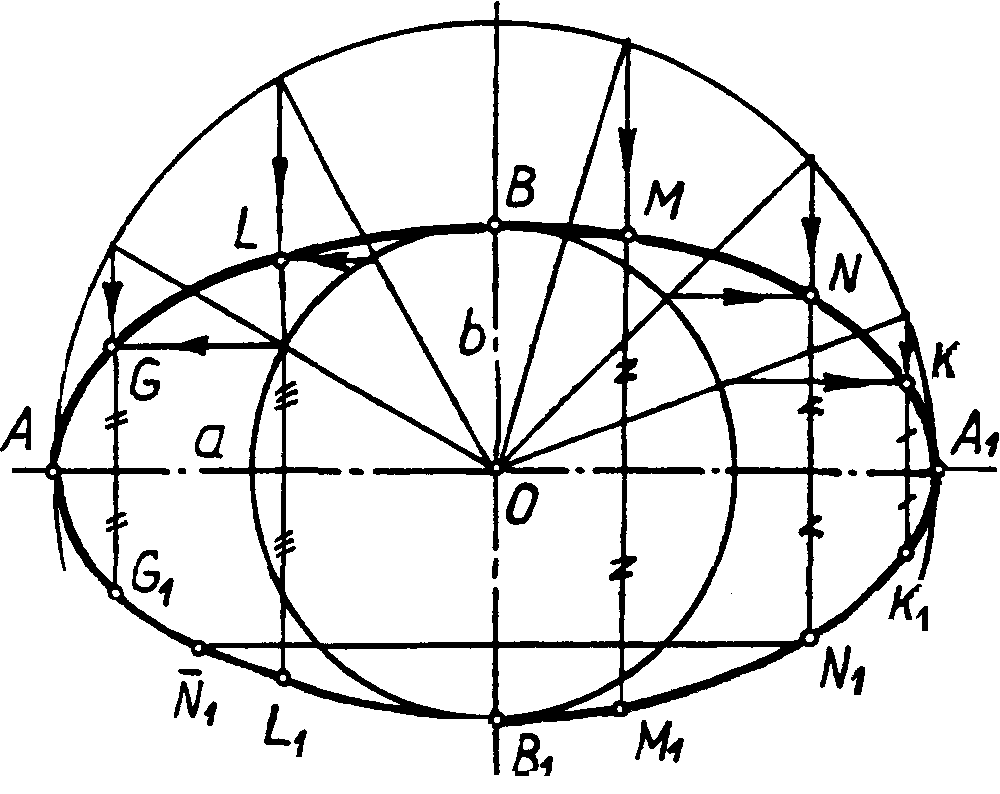 ис.2 Рис.2 1 1i-2i // P-Q .2. Построение гиперболы по ее вершинам А и А1 и точке М /рис.3/. 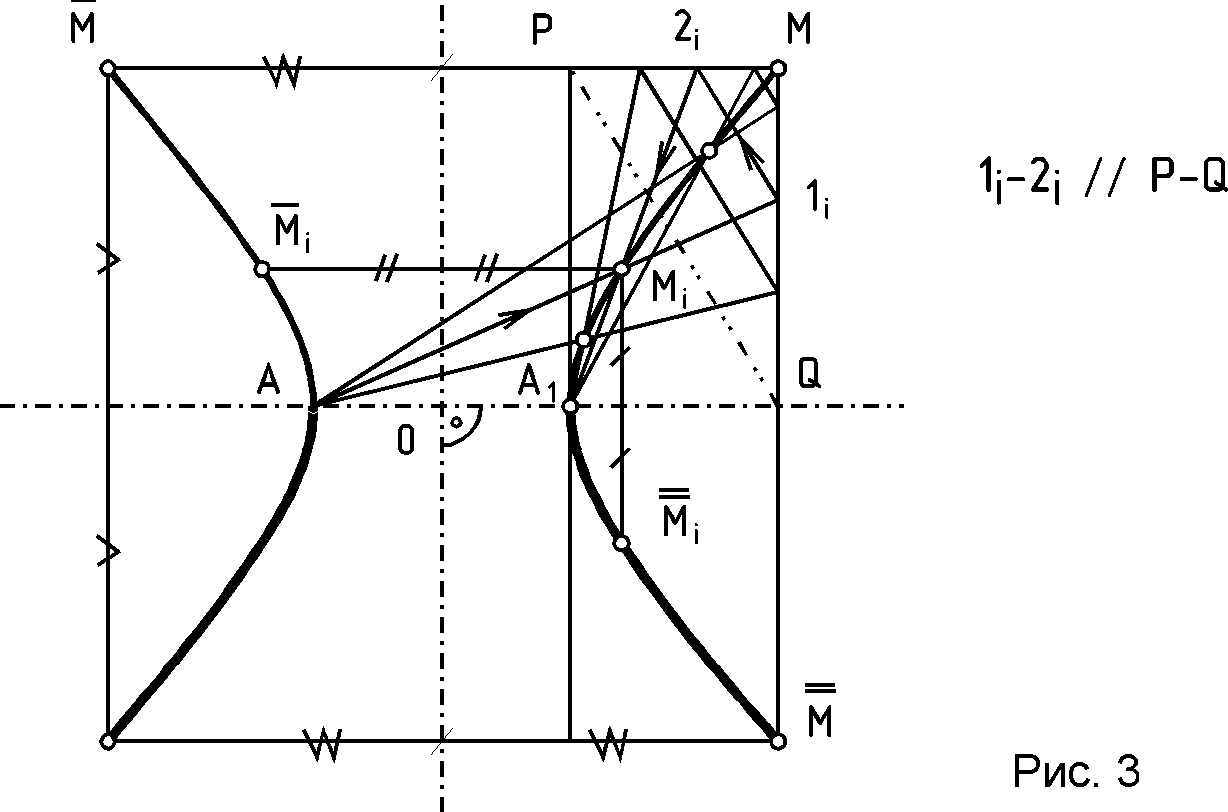 1.3 Построение параболы по ее вершине A, точке M и оси I /рис.4/. 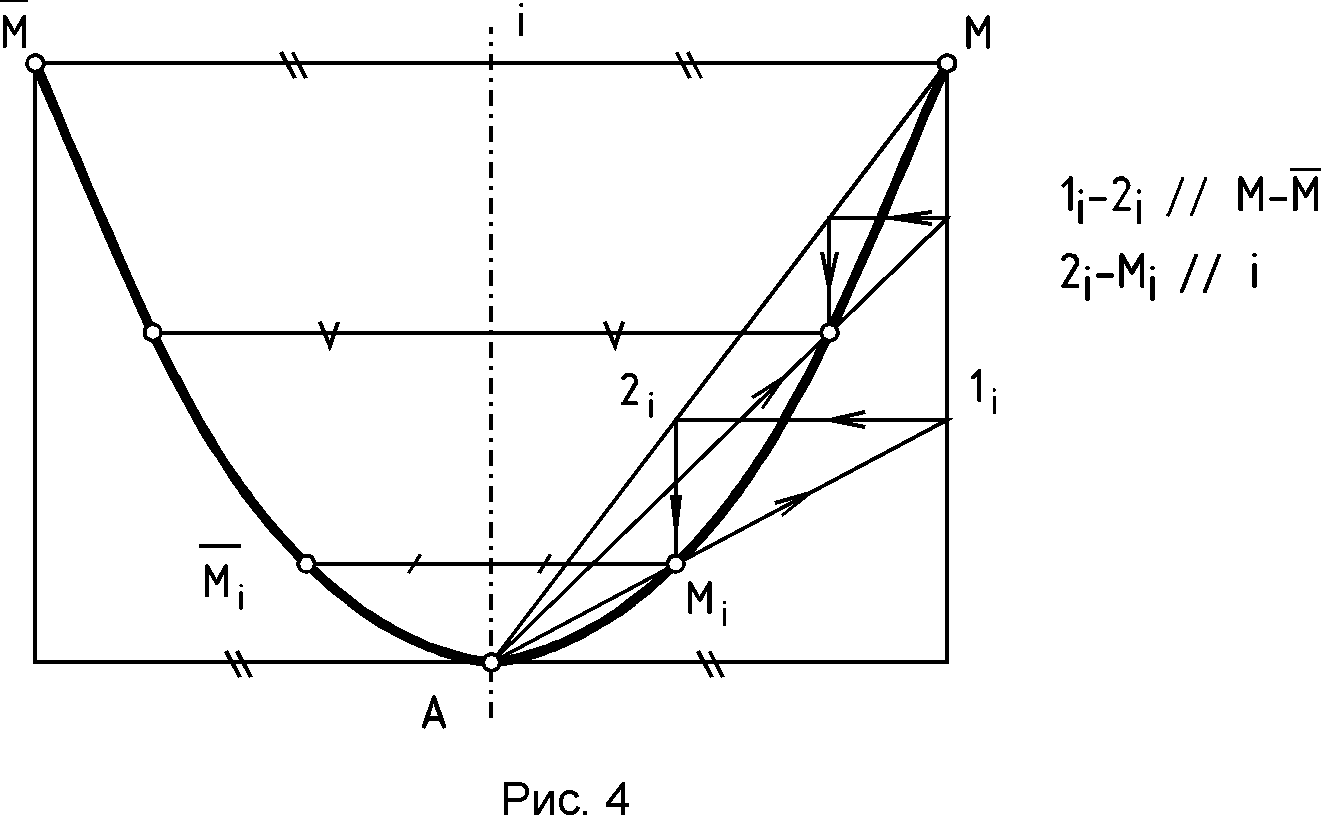 Более подробно о способах построения кривых линий второго порядка смотрите в литературе /1, 2/. 1.4. Построение очерков поверхностей вращения, оси которых параллельны одной из плоскостей проекций Задачи на построение очерков поверхностей вращения, оси которых параллельны одной из плоскостей проекций и наклонены к другим плоскостям проекций решаются с помощью вспомогательных сфер, которые выбираются касающимися заданной поверхности вращения вдоль ее параллелей. Пример 1.4.1./рис.5/. Построить профильную проекцию конуса вращения, ось i которого параллельна фронтальной плоскости проекций и наклонена к двум другим плоскостям проекций. Для построения образующих поверхности конуса на профильной плоскости проекций воспользуемся вспомогательной сферой с центром в точке 0" и касательной к конической поверхности по параллели Т"Т1" . Профильная проекция сферы, описанная из точки 0", позволит провести касательные S"' К"' и S"'K1"' известными из планиметрии геометрическими приемами П 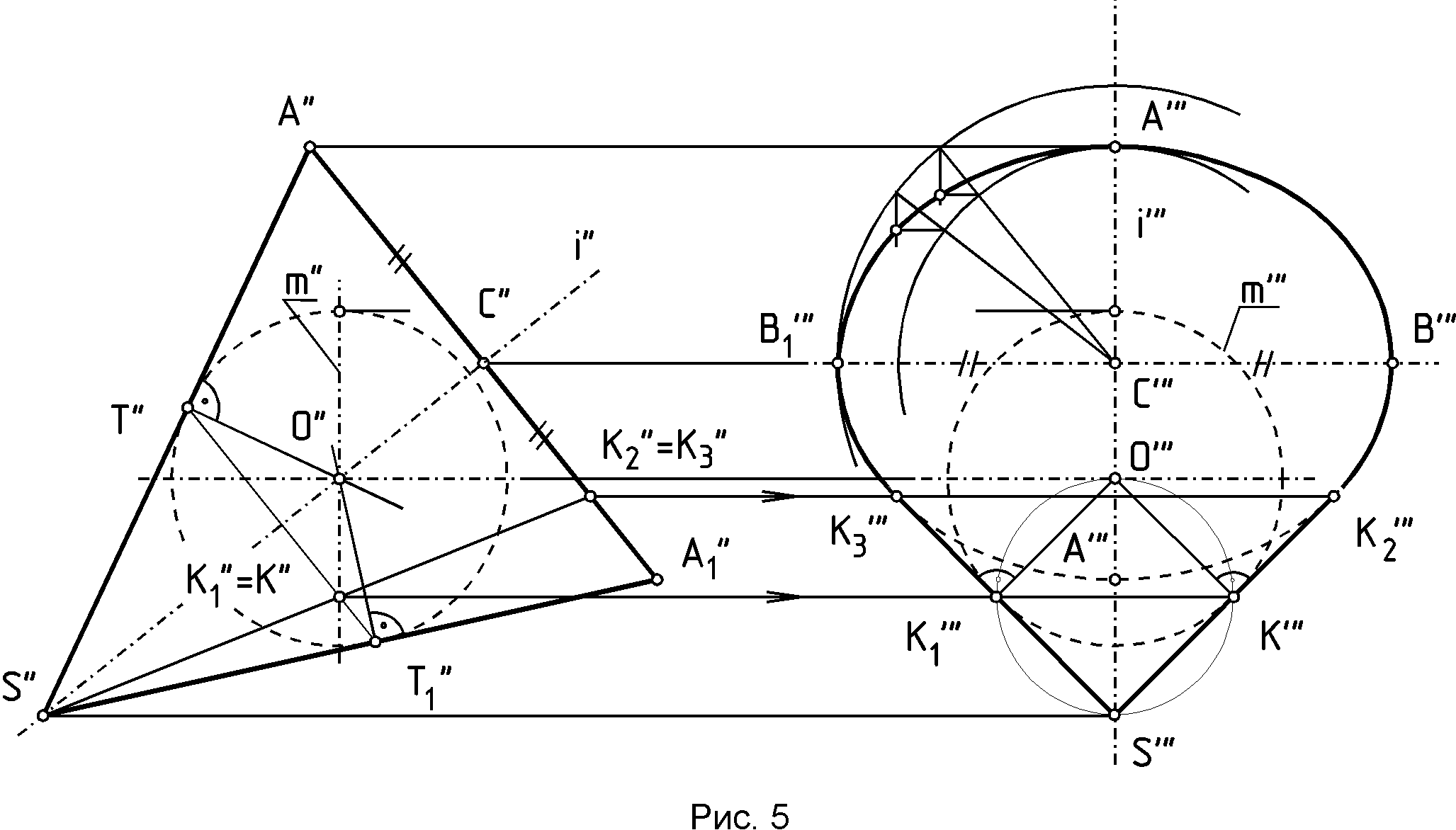 рофильную проекцию основания конуса - эллипс А"' В"' А1"' В1"' - можно построить по его главным осям, одним из известных способов, один из которых показан на чертеже. Пример 1.4.2./рис.6/. Построить профильную проекцию отсека параболоида вращения, ось i которого параллельна фронтальной плоскости проекций и наклонена к двум другим плоскостям проекций под некоторыми углами. Как известно, очерком поверхности второго порядка в общем случае является линия второго порядка, представляющая собой плоскую кривую /в данном случае - параболу/. Очерк фронтальной проекции параболоида вращения - парабола М"Мi"А"М1" на чертеже построен с помощью найденных промежуточных точек типа Мi" указанным на чертеже способом. 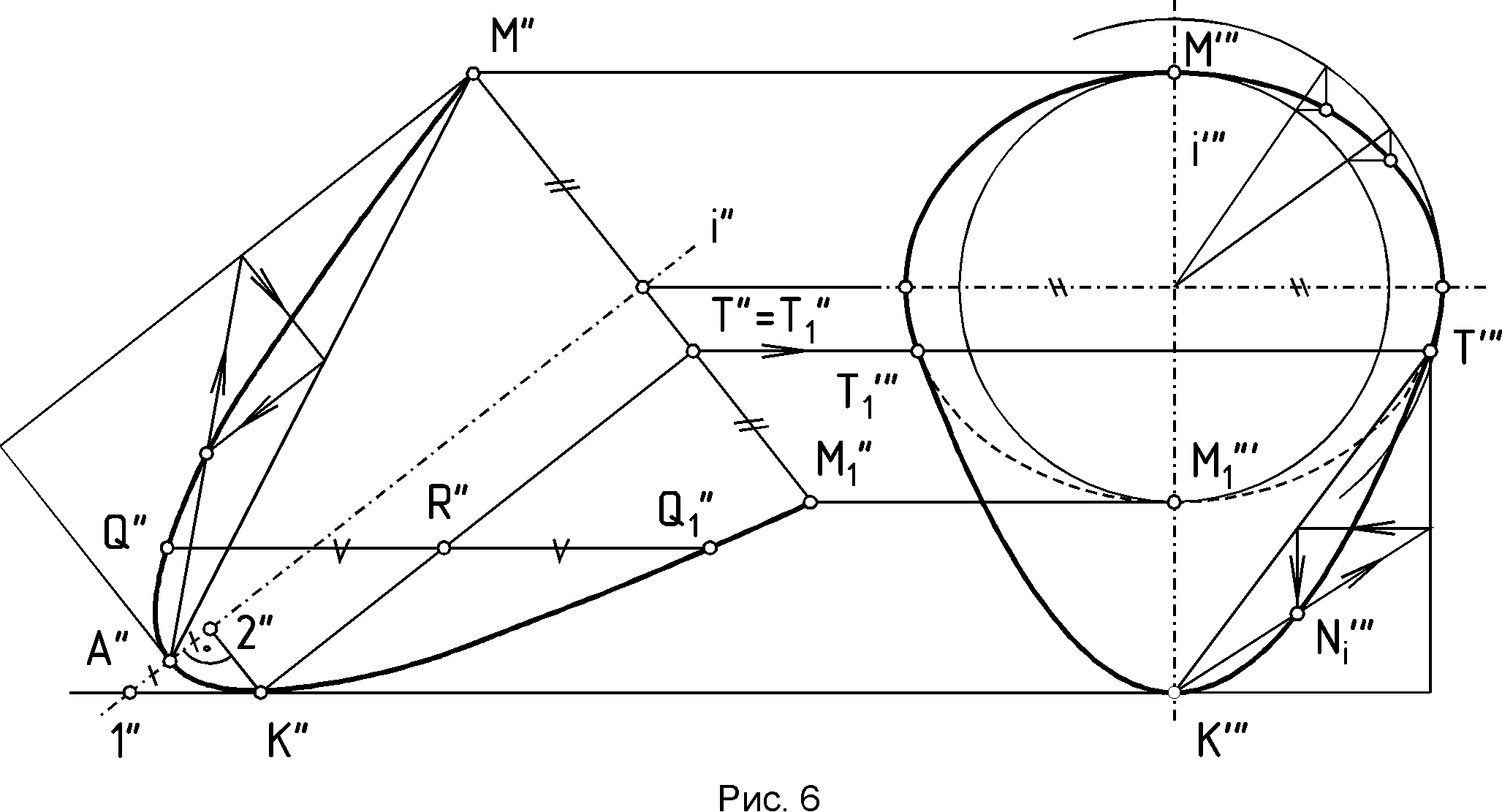 Проекция поверхности параболоида вращения на профильной плоскости проекций определяется очерком Т"' Ni"' K"' T1"' представляющим собой параболу, промежуточные точки этого очерка - точки типа Ni"' - найдены тем же приемом, что и точки типа Mi". Точку К" можно найти с помощью сопряженного диаметра параболы Q" Q1" , найдя середину которого - точку R", можно провести другой, сопряженный с первым, диаметр параболы К" Т", проходящий через точку R" и параллельный оси i" параболы М", Mi", А", К", M1", найдя профильные проекции точек Т " и T1" на очерке основания отсека параболоида вращения. Для нахождения точки K" можно воспользоваться свойством касательной к параболе, для которой характерно то, что проекция касательной на ось параболы /подкасательная/ делится вершиной А" параболы пополам. Таким образом, отмерив от точки А" по направлению оси i" параболоида отрезок А"2" равный отрезку 1"А". Найдя точку 2" и восстановив из нее перпендикуляр к оси i", можно найти точку K", через которую и пройдет контурная линия K"T"=T1" поверхности параболоида вращения при построении очерка этой поверхности на профильной плоскости проекций. Эта линия будет границей видимости поверхности параболоида вращения на профильной плоскости проекций. Зная точки К", Т" и Т1" можно построить очерк отсека параболоида вращения на профильной плоскости проекций известным способом, показанным на чертеже. Пример,1.4.3. /рис.7/. Построить профильную проекцию отсека закрытого тора, ось i" которого параллельна фронтальной плоскости проекций и наклонена к профильной плоскости проекций под некоторым углом. Образующая тора - дуга A"1"S" окружности радиуса А"С1" = А1"С". Для решения задачи воспользуемся методом вспомогательных сфер с центрами в точках 0", 01" , 02"..., вписанных в поверхность отсека тора. Например, сфера с центром в точке 0" касается очерка тора в точках 1" и 11" а его поверхности - по параллели диаметра 1"11" . Эта параллель пересечет меридиан 2"21" сферы, параллельный профильной плоскости проекций, в точках К" и К1", профильные проекции К" и К1" которых соответствующей проекции этого меридиана будут принадлежать очерку профильной проекции отсека закрытого тора. 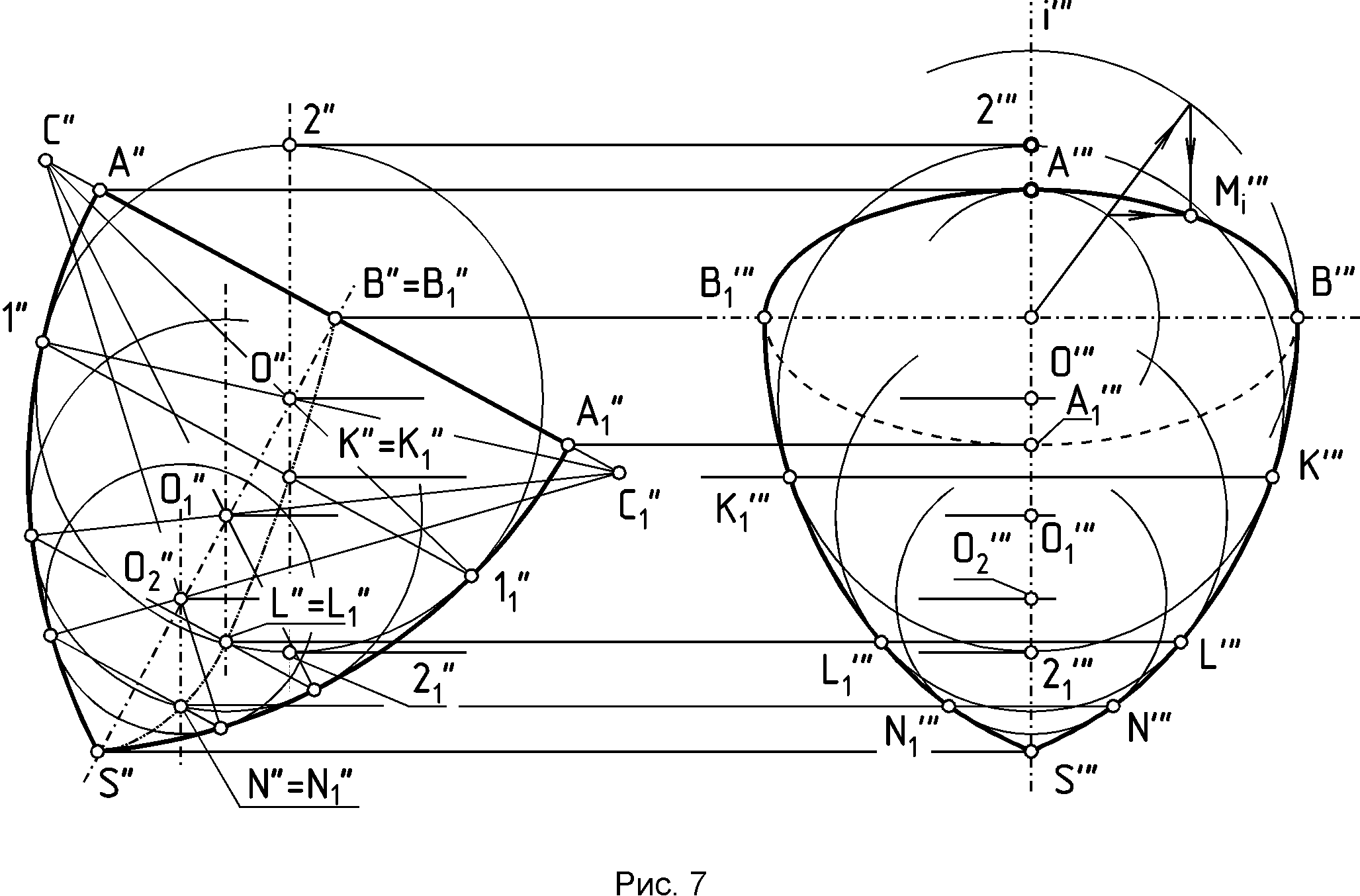 Найдя аналогичным способом точки L" и L1", N" и N1", S"', можно построить огибающую профильных проекций вписанных в отсек закрытого тора сфер - кривую В"', K"', L"', N"', S"', L1"', К1"', В"1 - очерк отсека тора на профильной плоскости проекций. Контурной линией этого очерка на фронтальной проекции тора будет линия В"=B1", К"=К1", L"=L1", N"=N1", S" являющаяся границей видимости профильной проекции отсека тора. 1.5. Проецирование линии пересечения двух поверхностей вращения второго порядка на плоскость, параллельную их общей плоскости симметрии, встречающиеся в домашнем задании эпюр №З.
Более подробно см. /2,с. 220-230; 4,с. 211-216/. 1.6. Проецирование линии пересечения поверхности второго порядка с поверхностью тора на плоскость, параллельную их общей плоскости симметрии, см. /2,с. 217-220/. 2. Краткие сведения о способах построения линий взаимного пересечения двух кривых поверхностей Две поверхности второго порядка в общем случае пересекаются по кривой четвертого порядка, которая может распадаться на две части. Иногда /см. теорему Монжа и другие случаи/ эта кривая линия может вырождаться в две плоские кривые второго порядка. Об этом будет сказано ниже. Обычно линию пересечения кривых поверхностей строят по точкам этой линии, которые могут быть найдены одним из двух принципиально отличных способов. Это способ вспомогательных секущих плоскостей и способ вспомогательных секущих сфер, как концентрических, так и эксцентрических. Эти вспомогательные секущие плоскости или сферы играют роль посредников. Наиболее рациональным способом решения задачи будет считаться тот, который дает простые линии пересечения поверхности-посредника с заданными поверхностями /окружности или прямые/, то есть инструментально простые линии. Выбор способа вспомогательных секущих плоскостей или вспомогательных секущих сфер зависит в первую очередь от тех свойств поверхностей, заданных, на чертеже и от их взаимного расположения. Например, если на чертеже заданы две поверхности вращения, оси которых перпендикулярны к одной из плоскостей проекций, или две поверхности, одна из которых имеет образующие, параллельные некоторой плоскости проекций, а вторая поверхность является поверхностью вращения, ось которой перпендикулярна к этой плоскости проекций и т.п., то в этом случае может быть применен способ вспомогательных секущих проецирующих плоскостей. В случае задания на чертеже двух поверхностей вращения, оси которых пересекаются и параллельны одной из плоскостей проекций или перпендикулярны к различным плоскостям проекций, может быть применен способ вспомогательных секущих концентрических сфер, а при некоторых других условиях взаимного расположения поверхностей и при определенных свойствах их плоских сечений могут быть применены и другие способы решения задач. Рассмотрим примеры применения указанных способов. 2.1. Способ вспомогательных секущих плоскостей Пример 2.1.1. /рис.8/. Построить в трех проекциях линию пересечения поверхностей двух тел вращения - конуса и тора, имеющих общую плоскость симметрии, параллельную фронтальной плоскости проекций и оси вращения, параллельные оси х. 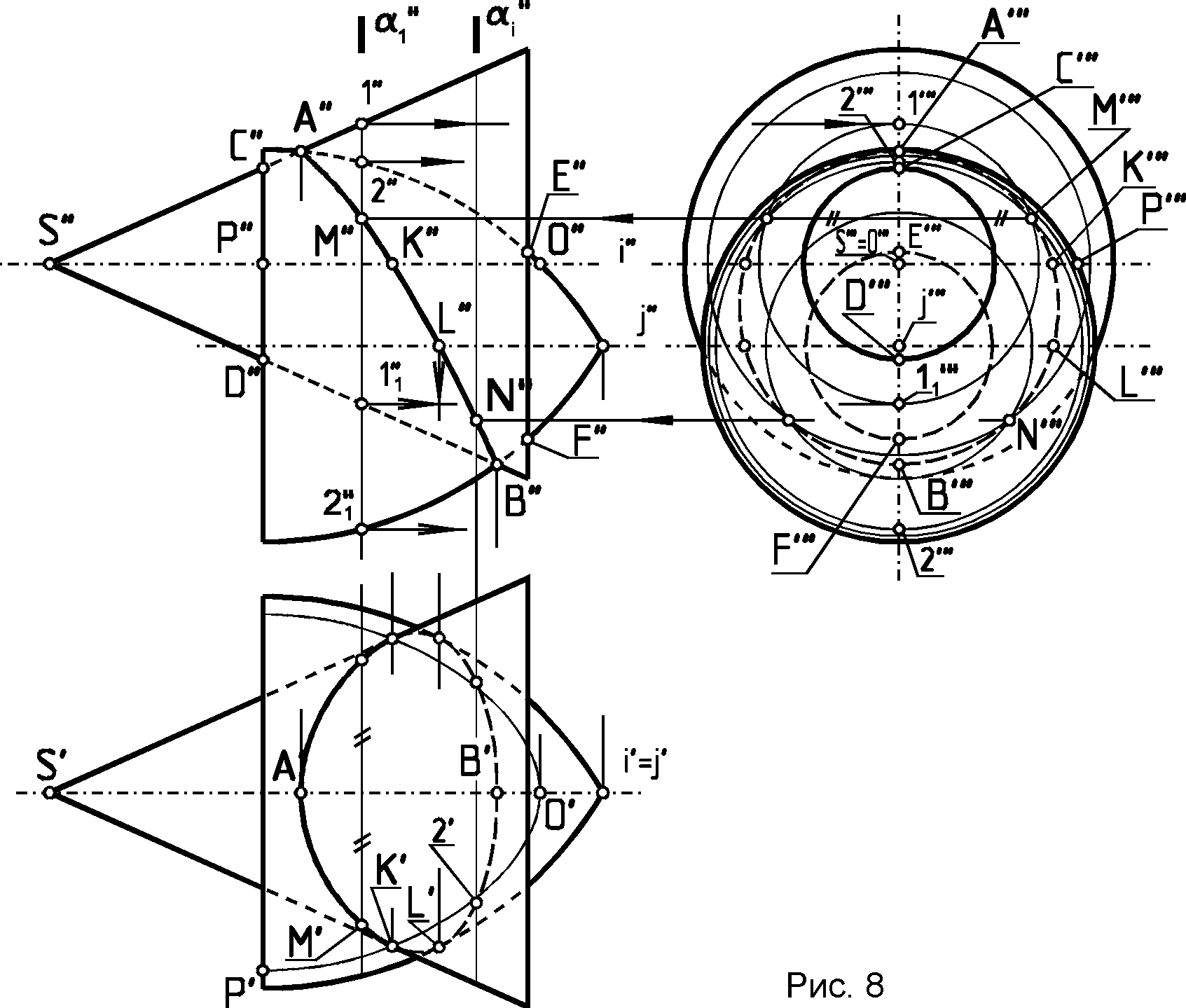 После нахождения характерных или опорных точек искомой линии пересечения - точек: А, В, С, D, Е, F пересечения очерковых образующих, находим промежуточные точки искомой линии. Для этого воспользуемся вспомогательными секущими плоскостями 1/1"/... i/i"/, пересекающими заданные поверхности по параллелям. Например, плоскость 1, пересечет конус по параллели 1-11 , а тор - по параллели 2-21 , общие точки М и М1, которых будут принадлежать искомой линии пересечения заданных поверхностей, а плоскость i позволит найти точки N и N1, этой линии. Найдя необходимое и достаточное количество точек, а в их числе и точки типа К и L, принадлежащие очерковым образующим, а также окружности диаметров CD и EF пересечения оснований тел вращения с поверхностями, можно провести искомые линии. Пример 2.1.2. /рис.9/. Построить в трех проекциях линию пересечения поверхностей конуса и цилиндра. Данная задача относится ко второму типу задач на взаимное пересечение двух поверхностей, так как одна из заданных поверхностей /цилиндрическая/ - профильно проецирующая. И 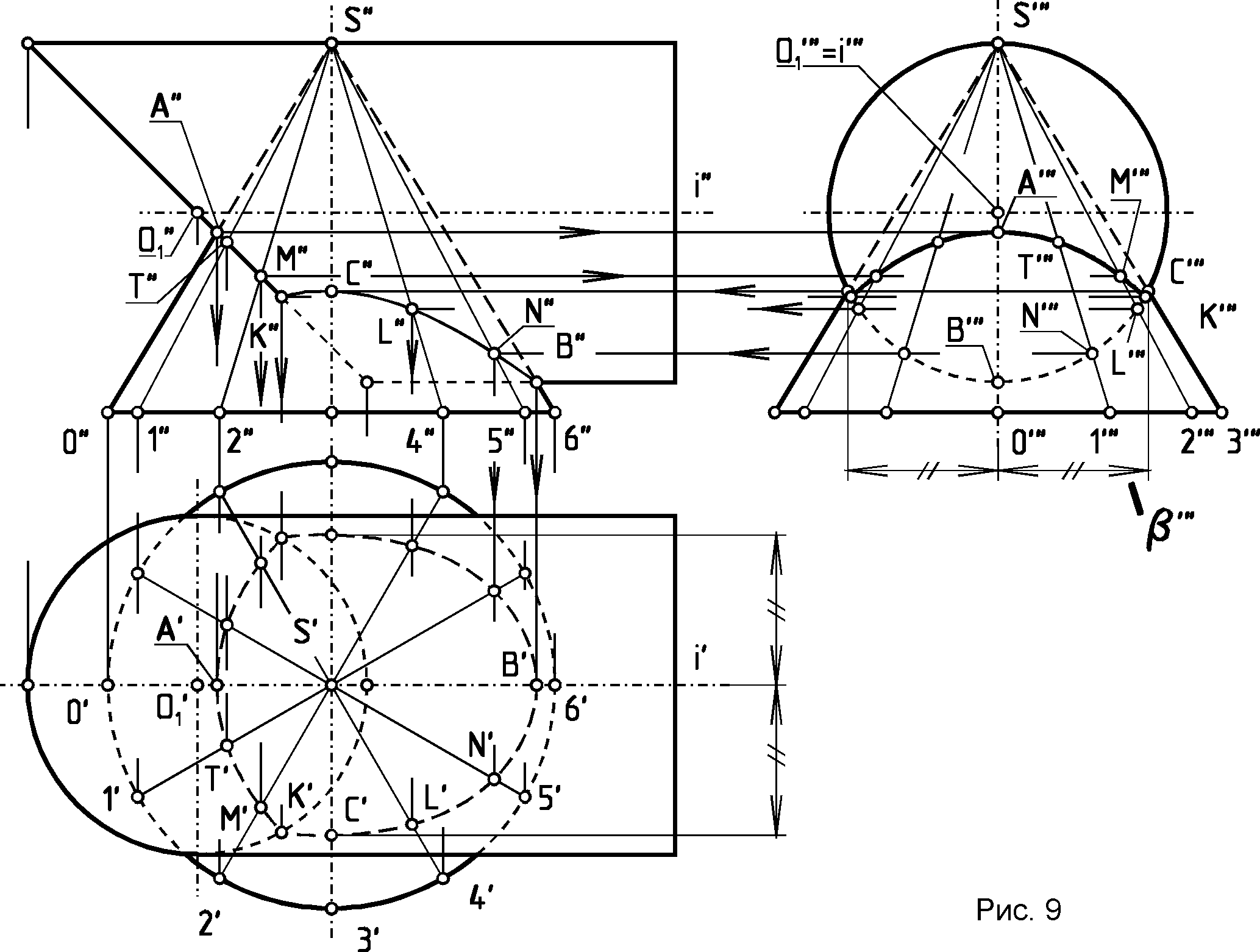 звестно, что в данном случае одна из проекций искомой линии пересечения /или ее часть/ на чертеже уже есть. В данном случае это линия С"'...В"'...С1"'. Другие проекции этой линии можно построить по принадлежности точек этой линии соответствующим образующим второй /конической/ поверхности. Сначала найдем характерные точки искомой кривой пересечения поверхностей - точки А, В, С и С1, лежащие на очерковых образующих. Затем, для упрощения решения задачи и последующего построения развертки /эпюр ЗБ/ построим равномерный каркас из 12, 16 или 24 образующих конуса в зависимости от размеров чертежа и найдем точки пересечения этих образующих с цилиндрической поверхностью, а также точки типа М, М1.. пересечения образующих с основанием цилиндра и, соединив их последовательно от одной образующей к другой, получим искомую линию пересечения заданных поверхностей. В данном случае применение вспомогательных секущих плоскостей типа плоскости /"'/ - отпадает. Пример 2.1.3. /рис.10/. Построить в трех проекциях линию пересечения двух поверхностей вращения второго порядка - цилиндра и конуса, - соприкасающихся в двух точках. В этом случае линия пересечения заданных поверхностей - кривая четвертого порядка - распадается на две плоские кривые линии, проходящие через эти точки /2, c.241-245; 3, с.163-155; 4, с.202-204/. Поскольку заданные поверхности на чертеже имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций, эти линии пересечения на эту плоскость будут проецироваться в виде прямых линий. Проекции этих линий на других плоскостях проекций находятся по принадлежности либо к образующим цилиндра, либо к образующим конуса. Построение аналогично решению предыдущей задачи и понятно из приведенного чертежа. 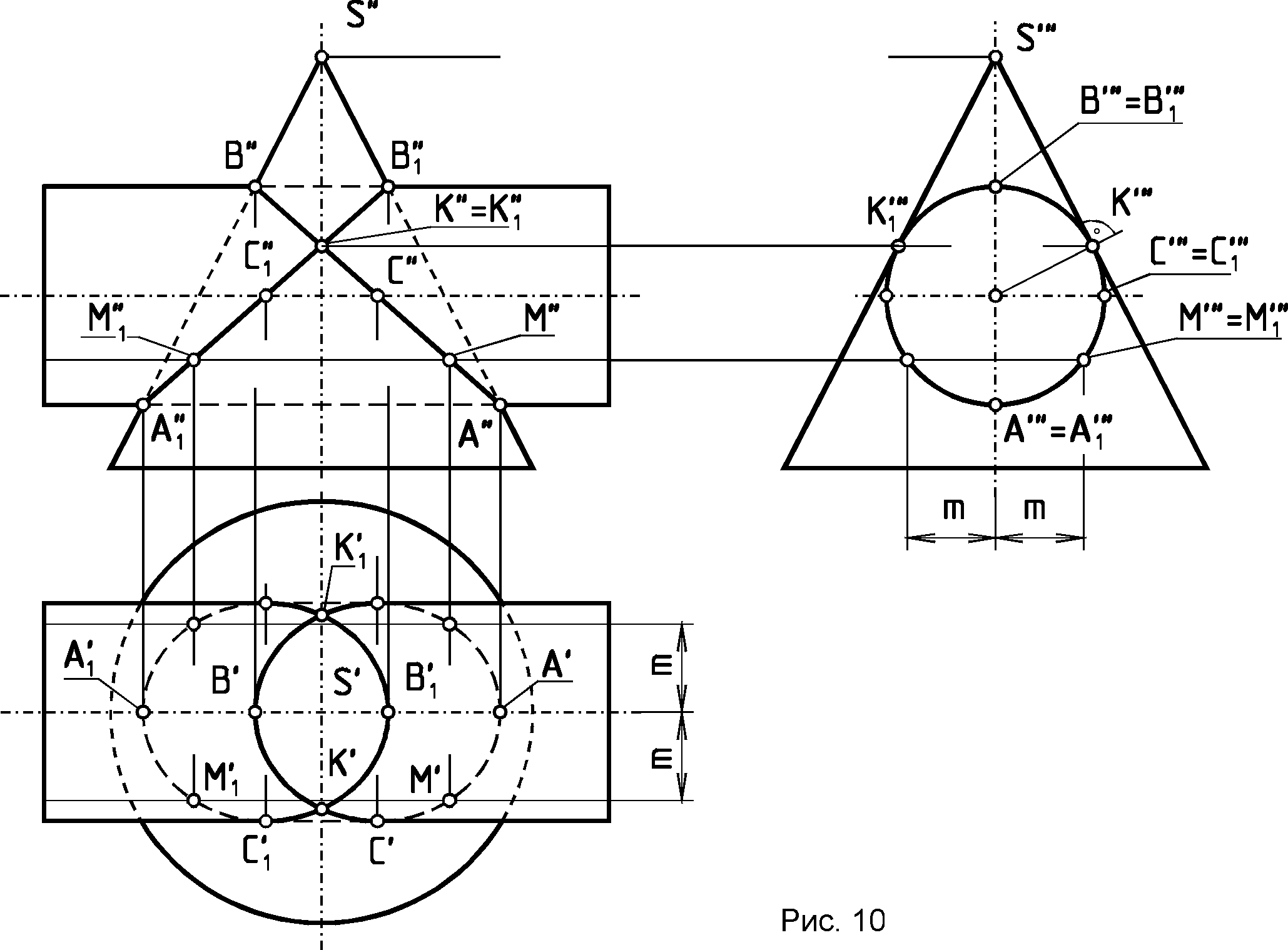 2.2. Способ вспомогательных секущих концентрических сфер. Если на чертеже заданы две поверхности вращения, оси которых пересекаются и параллельны одной из плоскостей проекций, то линию пересечения этих поверхностей можно построить способом вспомогательных секущих концентрических сфер с центром в точке пересечения осей. Пример 2.2.1. /рис. 11/. Построить линию пересечения поверхности отсека закрытого тора с поверхностью конуса вращения, оси которых пересекаются и параллельны фронтальной плоскости Находим опорные точки А и В искомой кривой пересечения. Приняв точку пересечения осей заданных поверхностей вращения за центр вспомогательных секущих сфер, которые пересекут обе поверхности по их параллелям, опишем ряд сфер. Например, сфера радиуса R 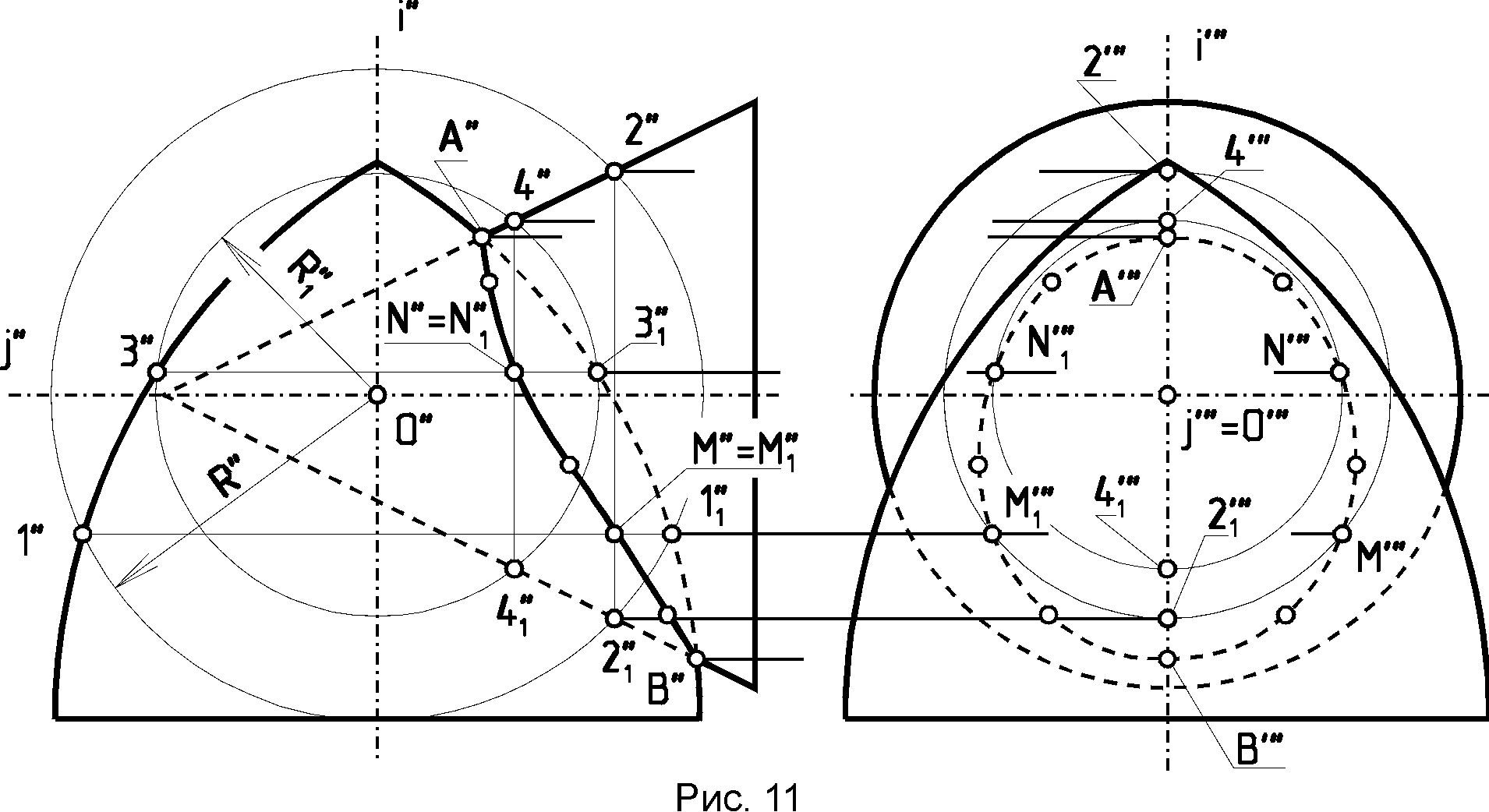 пересечет поверхность тора по параллели 1"-1" , а конус - по параллели 2"-2", которые пересекаются между собой в точках М" и М1" , принадлежащих искомой линии пересечения заданных поверхностей. Профильные проекции этих точек находим по принадлежности этих точек проекции параллели - окружности диаметра 2"'-2"' , проведя линию связи M"-M"'. Аналогичным образом с помощью сферы радиуса R1,определены точки N и N1 искомой линии пересечения, а затем - другие точки искомой линии пересечения заданных поверхностей. 2.3. Способ вспомогательных секущих эксцентрических сфер Если на чертеже будут заданы две поверхности с общей плоскостью симметрии, параллельной одной из плоскостей проекций , одна из которых является поверхностью вращения, а другая поверхность будет иметь семейство плоских круговых сечений, перпендикулярных к общей плоскости симметрии, то линию пересечения этих поверхностей можно построить по точкам, найденным с помощью вспомогательных секущих эксцентрических сфер. П 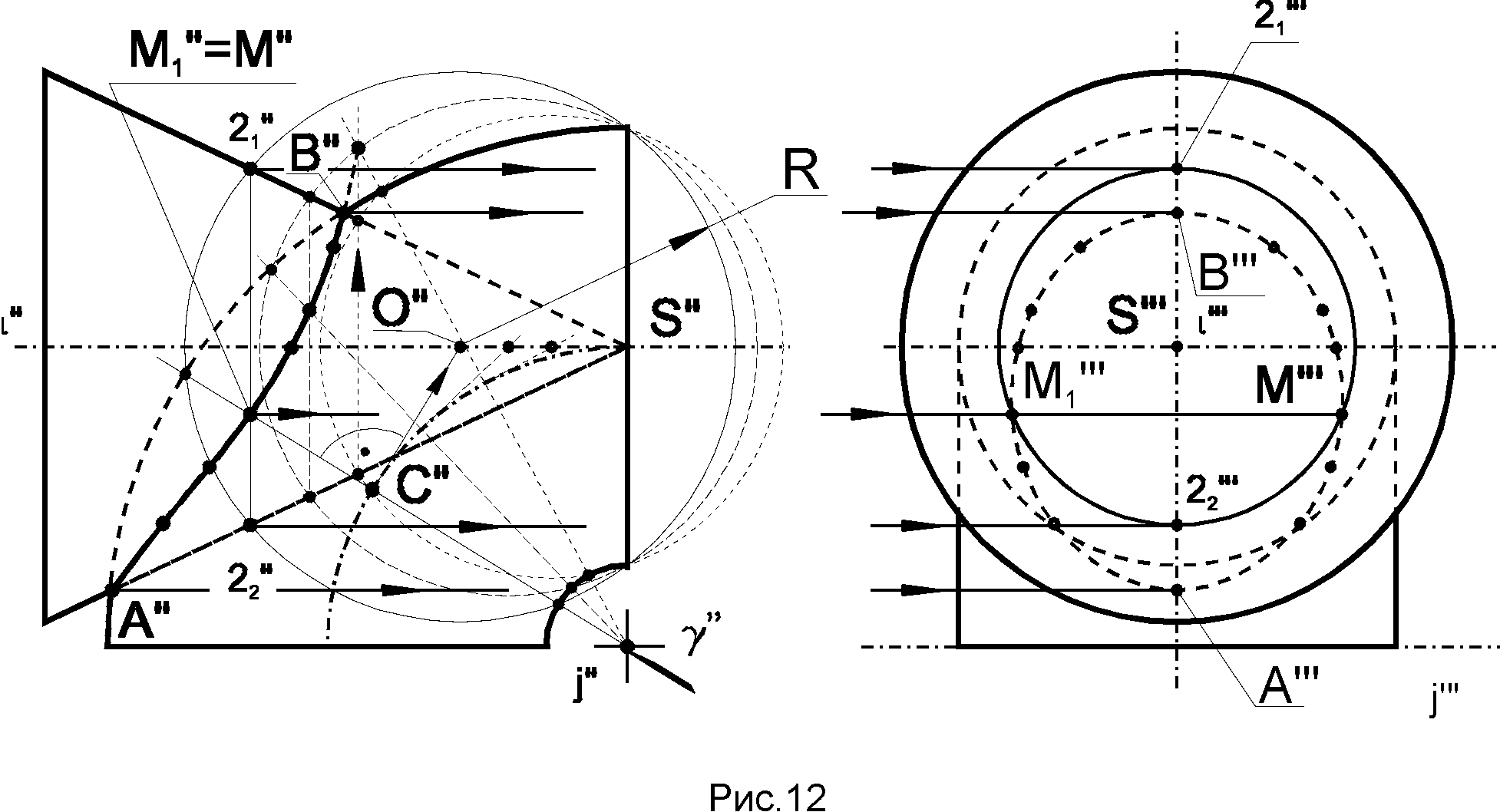 ример 2.3.1. /рис. 12/. Построить линию пересечения конуса вращения с отсеком тора /кругового кольца/, имеющих общую плоскость симметрии, параллельную фронтальной плоскости проекций. Находим опорные точки А и В искомой линии пересечения. Плоскость, в которой перемещается центр окружности, образующей /производящей/ при своем движении поверхность тора, совпадает с главной меридиональной плоскостью конуса вращения. Учитывая это, образующую /производящую/ окружность тора, например, если она расположена в плоскости , можно принять за линию пересечения тора вспомогательной секущей сферой. При этом центр этой сферы - точку 0"- следует выбирать на оси конуса в месте пересечения перпендикуляра, восставленного из центра С" к плоскости окружности, до пересечения с осью i конуса вращения. Аналогичным образом, выбирая в интервале между опорными точками А" и В" новые окружности сечения тора и проводя соответствующие сферы, найдем необходимое и достаточное количество точек искомой линии пересечения заданных поверхностей. 3. Развертки кривых поверхностей Кривые поверхности, которые полностью, без растяжения или сжатия, без разрывов и складок можно совместить с плоскостью, называют р а з в е р т ы в а е м ы м и. К этим поверхностям относятся лишь линейчатые и только такие, у которых смежные образующие пересекаются между собой или параллельны. Этим свойством обладают т о р с ы /поверхности, образованные прямыми, касательными к направляющей пространственной кривой/, конические и цилиндрические поверхности. Остальные линейчатые поверхности, а также все нелинейчатые являются н е р а з в е р т ы в а е м ы м и.3.1. Построение развертки прямого, кругового усеченного цилиндра вращения /рис.13/ Для построения развертки цилиндра достаточно представить его как призму с большим количеством граней /практически достаточно 12-16 таких граней / равномерно разделив окружность основания цилиндра на равное число частей. Если на поверхности цилиндра расположена какая-либо линия, то на развертку цилиндра эту линию можно перенести по точкам, принадлежащим соответствующим образующим этой поверхности. 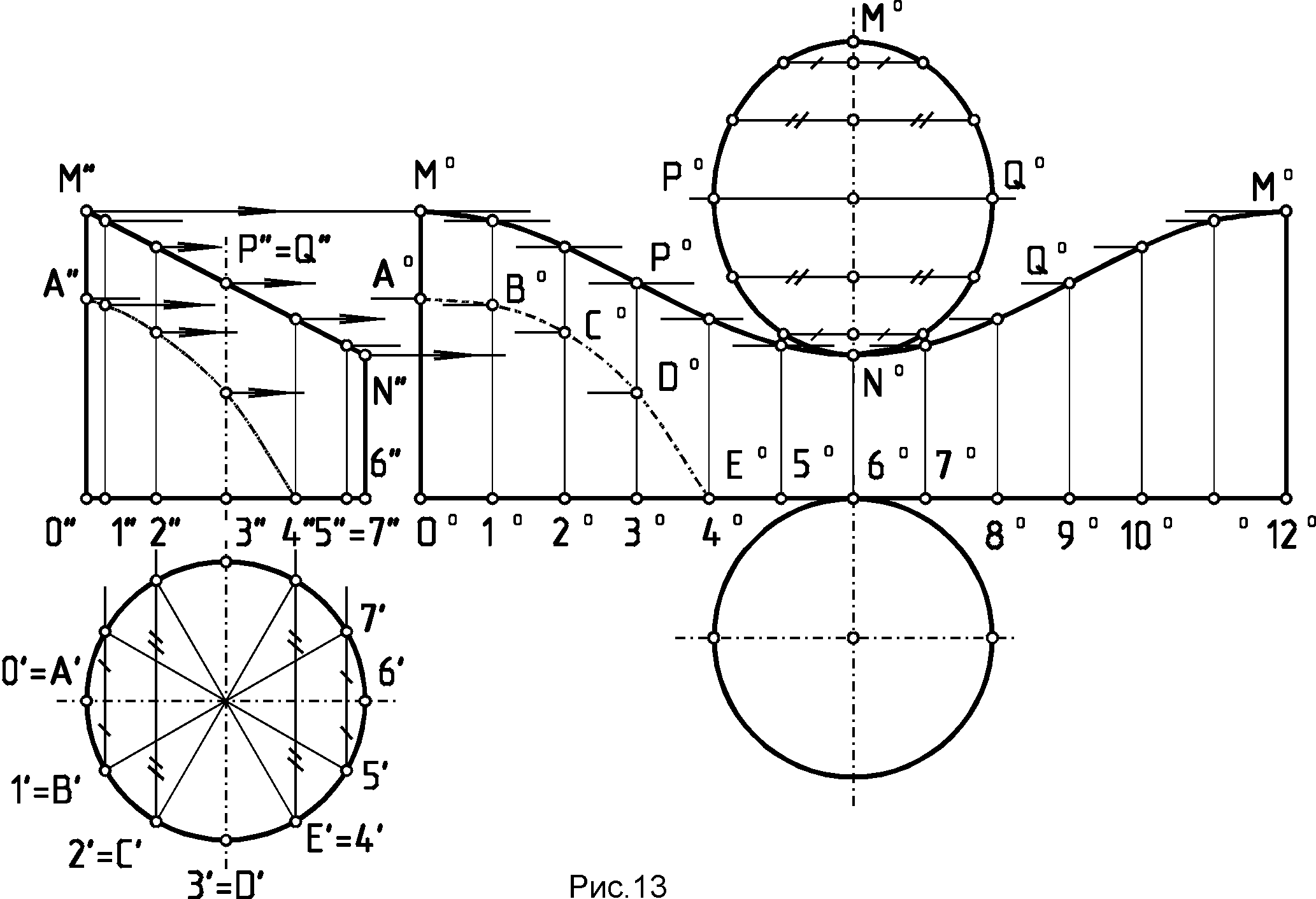 3.2. Построение развертки полной поверхности прямого кругового конуса /рис.14/ Для построения развертки прямого кругового конуса достаточно представить его поверхность как правильную пирамиду с большим числом граней и далее построить ее развертку, найдя натуральную величину одной из граней, представляющей coбой равнобедренный треугольник, по его боковой стороне и основанию. Построение развертки конуса видно из чертежа, где основание "грани" S01 равно хорде 0'1'. Развертка боковой поверхности конуса, в данном случае, содержит 12 таких "граней". Развертка боковой поверхности будет найдена точнее, если определить угол 0 при точке S на развертке по формуле: 0= (R/l)*3600, где: R- радиус основания конуса, a l- длина образующей конуса. 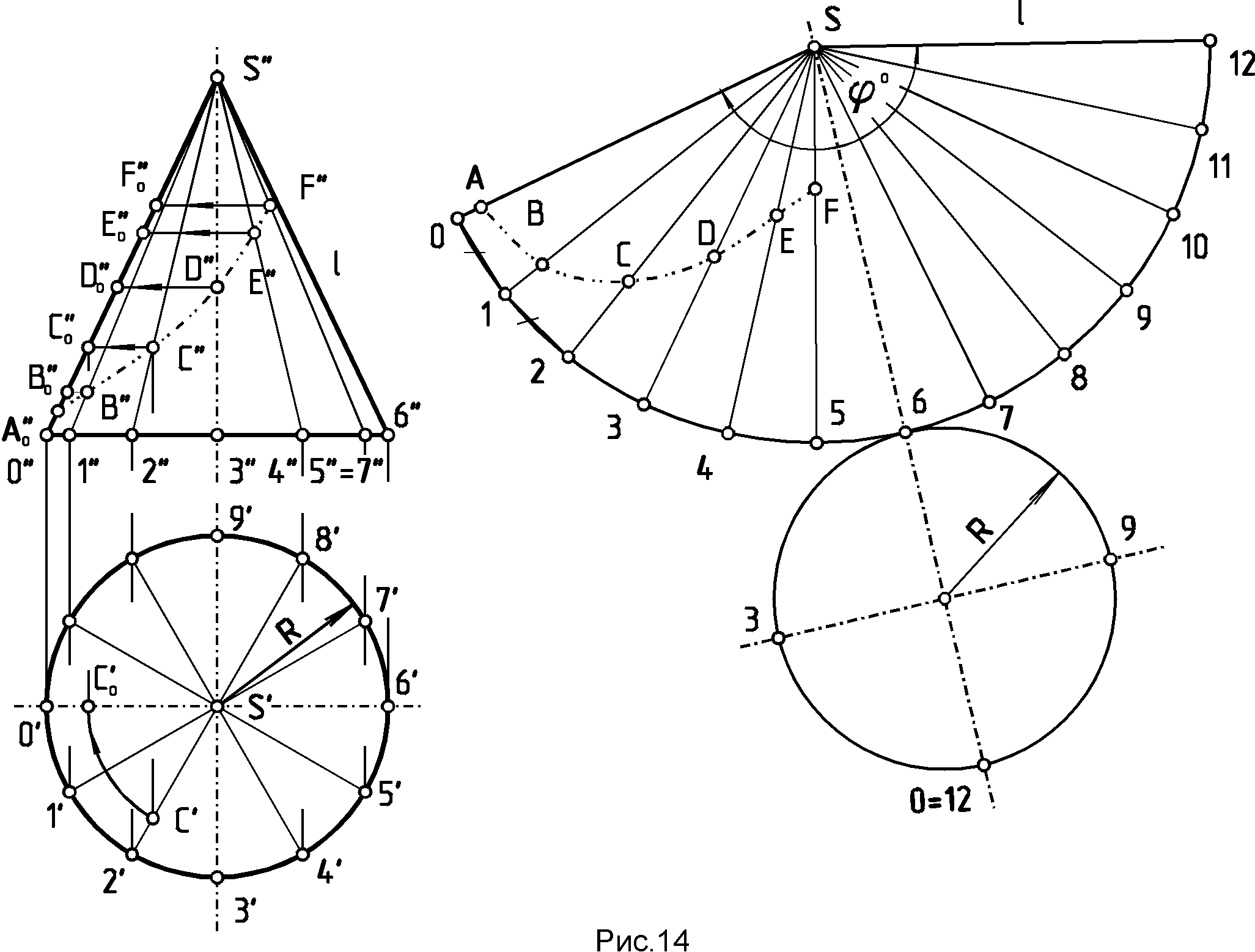 Принадлежащие боковой; поверхности конуса точки некоторой: кривой ABCDEF можно найти по принадлежности этих точек соответствующим: образующим конической поверхности. Для этого достаточно способом вращения, как показано на примере точки С, принадлежащей образующей S2, найти отрезки SB0"=SB, S"B0"=SB, S"E0"= SE т.п. Найденные отрезки отложить по соответствующим образующим на развертке конуса и провести через них линию ABCDEF. Для получения полной развертки конуса ее нужно дополнить основанием конуса, касательным в соответствующей точке развертки боковой поверхности. При построении развертки необходимо обратить внимание на то, чтобы внешняя поверхность конуса на развертке была обращена наружу, к наблюдателю, как указано на чертеже. Развертка боковой поверхности наклонного конуса находится как развертка наклонной пирамиды с большим количеством граней, каждую из которых находят по трем сторонам - двум боковым "ребрам" и "основанию" грани /2,с.447—449; 3, с.201-204, 4; с.227-229/. На рис. 15 представлен пример выполнения работы "Построение линии пересечения кривых поверхностей". 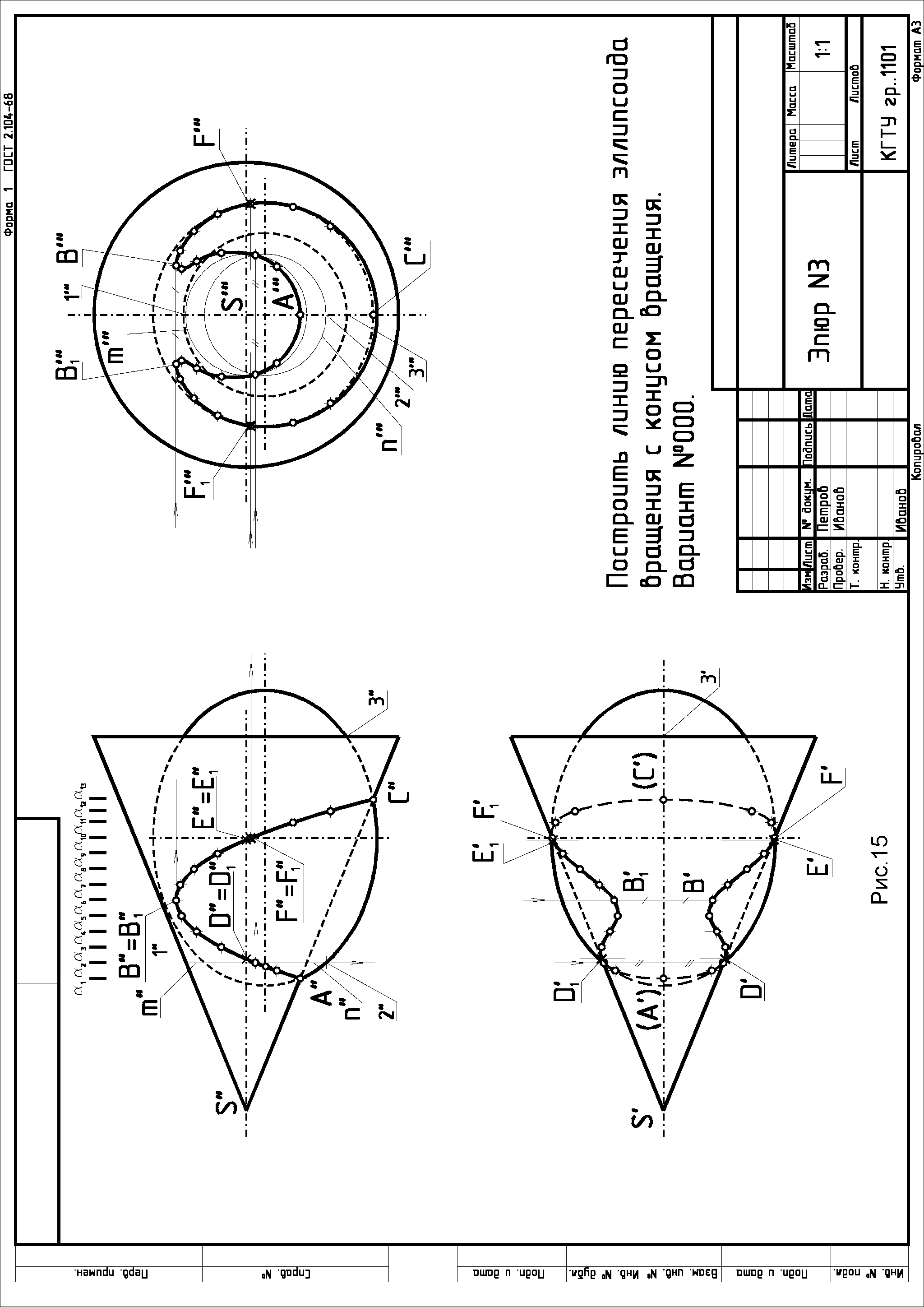 СПИСОК ЛИТЕРАТУРЫ1. Л е в и ц к и й В. С. Машиностроительное черчение: Учеб. для студентов высших технических учебных заведений. -М.: Высш. шк., 1988. - 351 с. 2. Б у 6 е н н и к о в A. В. Начертательная геометрия: Учеб. для вузов. - 3-е изд., перераб. и доп. - М.: высш. шк., 1985. - 288 с. 3. Фролов С. А. Начертательная геометрия: Учебник для втузов. - 2-е изд., перераб. и доп. - М.: Машиностроение,1983. - 240 с. 4. Г о р д о н В.О., С е к е н ц с в - О г и е в с к и й М. А. Курс начертательной геометрии: Учеб. пособие /Под ред. Ю.Б. Иванова. - 23-е изд., перераб. -М.: Наука. Гл. ред. физ,-мат., лит., 1988. - 272 с. |
