Контрольная работа интегралы Вариант 1. Решение. Для вычисления данного интеграла сделаем замену. После подстановки в интеграл получим Решение
 Скачать 254 Kb. Скачать 254 Kb.
|
|
Контрольная работа 1 Вариант №1 Найти неопределённые интегралы 1. Решение. Для вычисления данного интеграла сделаем замену После подстановки в интеграл получим:  2. Решение. Для вычисления данного интеграла преобразуем подынтегральную функцию и применим подстановку После подстановки в интеграл получим:  3. Решение. Для вычисления данного интеграла применим подстановку После подстановки в интеграл получим: 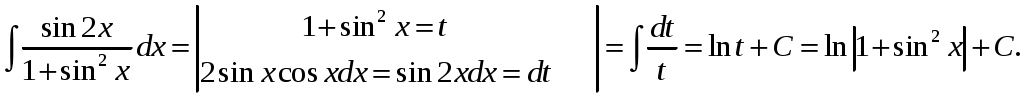 4. Решение. Для вычисления данного интеграла применим подстановку После подстановки в интеграл получим:  5. Решение. Применим формулу интегрирования по частям  6. Решение. Для вычисления данного интеграла необходимо сделать замену После подстановки в интеграл получим: 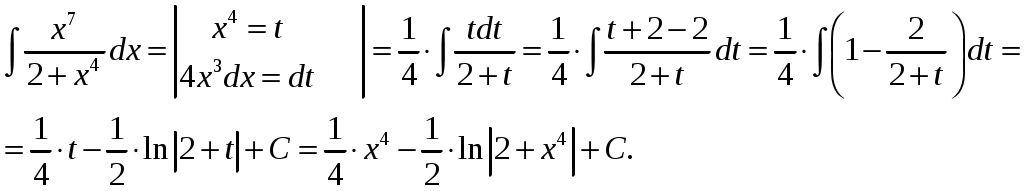 7. Решение. Применим подстановку 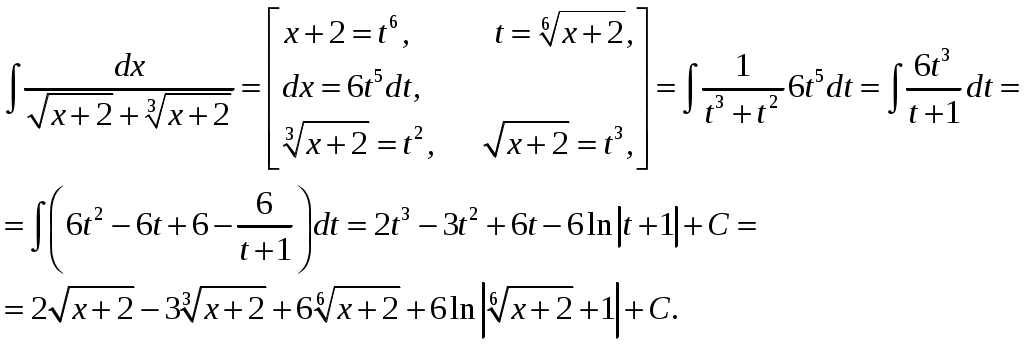 8. Решение. Применим формулу синуса двойного угла: 9.  . .Решение. Разложим подынтегральную функцию на сумму простейших дробей: 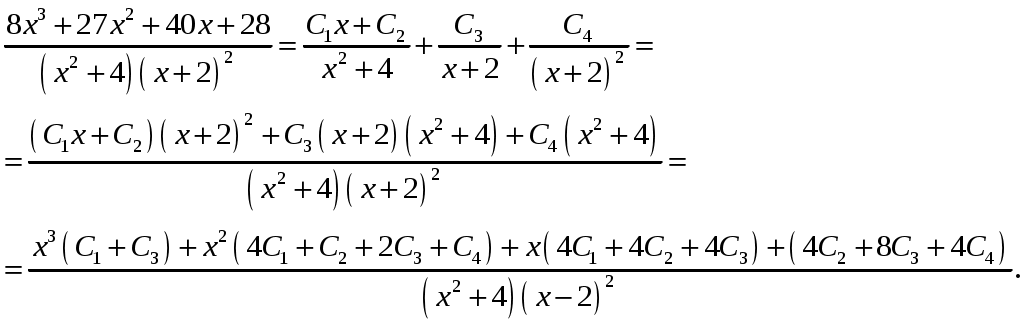 Коэффициенты найдем из условия: Приравняем коэффициенты с одинаковыми степенями при x:  откуда откуда 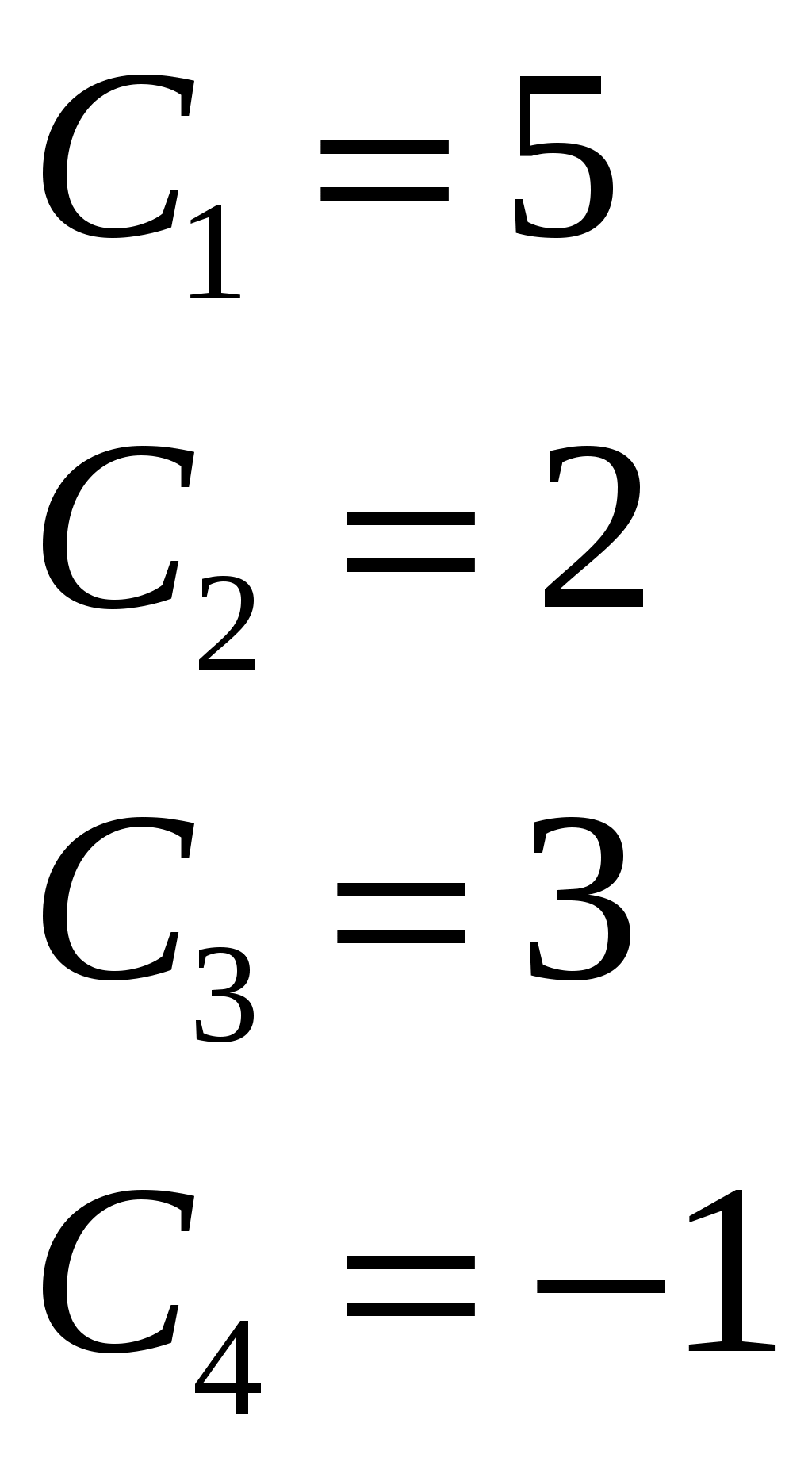 Таким образом, 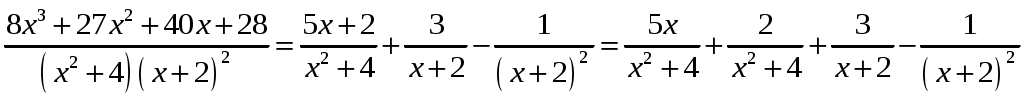  Вычислить определённые интегралы 10. 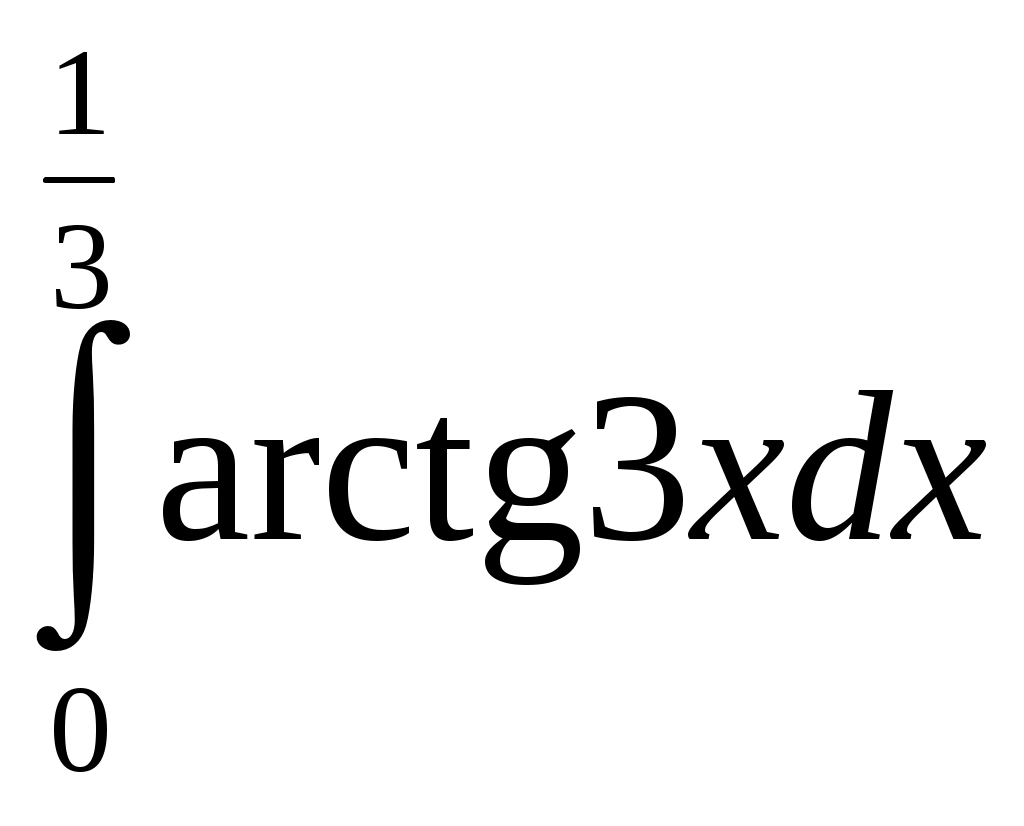 ; ; Применим формулу интегрирования по частям  Ответ: 11. Применим тригонометрическую формулу произведения косинуса на синус: 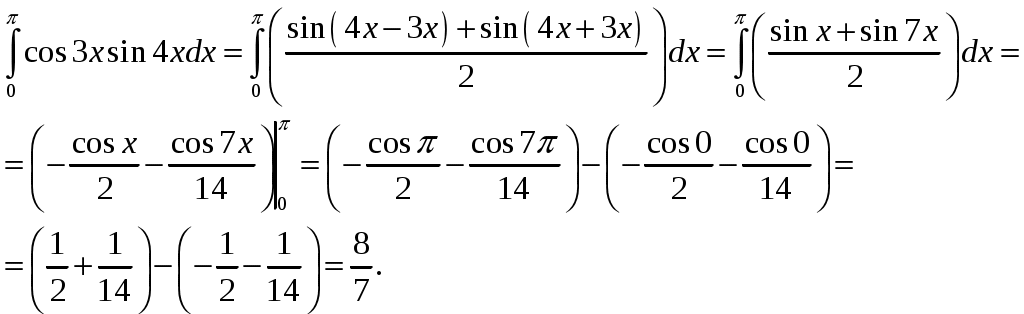 Ответ: Вычислить несобственные интегралы или установить их расходимость 12. Решение. Это несобственный интеграл I рода (с бесконечным пределом интегрирования). Согласно определению несобственного интеграла I рода  имеем 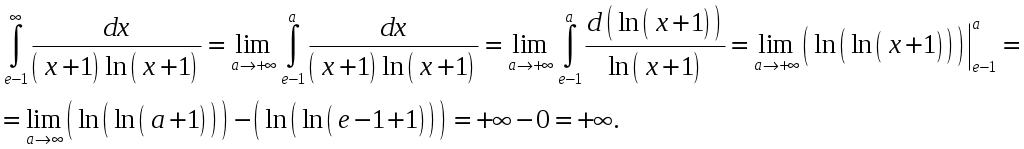 Ответ: интеграл расходится. 13. Это несобственный интеграл II рода. Согласно определению несобственного интеграла II рода 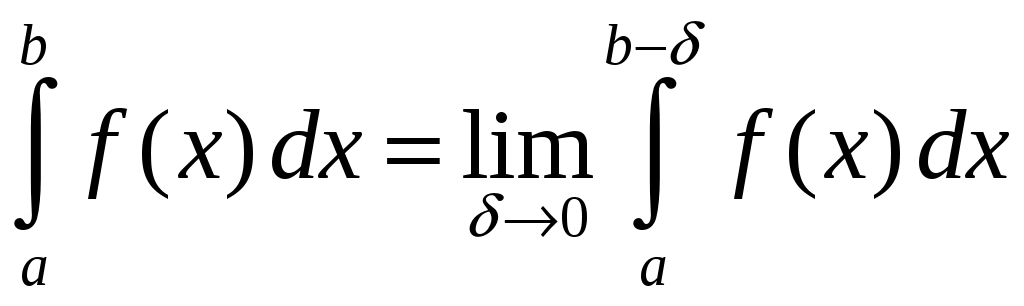 имеем Данный интеграл сходится. Ответ: интеграл сходится. Выяснить сходимость несобственных интегралов 14. Решение. Так как на промежутке  . .Поскольку интеграл в правой части неравенства сходится, то исследуемый интеграл тоже сходится согласно общему признаку сравнения несобственных интегралов. Ответ: интеграл сходится. 15. Так как при  Поскольку данный интеграл расходится, то исследуемый интеграл тоже расходится согласно общему признаку сравнения несобственных интегралов. Ответ: интеграл расходится. 16. Найти площадь области, ограниченной кривыми Решение. Координаты точек пересечения линий находим из системы:  Отсюда: Строим заданные линии на плоскости ХOУ. Составляем определенный интеграл: где 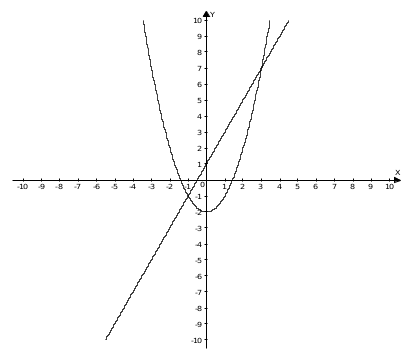 Искомая площадь:  Ответ. 17. Найти длину дуги кривой Решение. Длина дуги кривой заданной параметрическими уравнениями находится по формуле: Находим: Получаем: 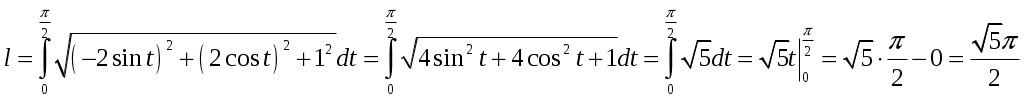 Ответ: Ответ: |
