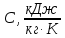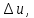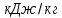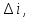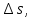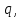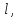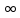Термодинамика, вариант №11 (Задачи №3 и №4). Решение Для заданных условий молярная изобарная теплоемкость азота n 2 составит Массовая изобарная теплоемкость азота
 Скачать 420.53 Kb. Скачать 420.53 Kb.
|
|
Контрольная задача №3 Азот N2, массой m = 44 кг, расширяется в цилиндре, перемещая поршень от начального давления 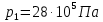 и температуры t1 = 375 и температуры t1 = 375 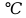 (T1 = 375 + 273 = 648 K) до конечного давления (T1 = 375 + 273 = 648 K) до конечного давления 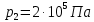 . . Требуется определить изменение внутренней энергии, работу расширения и теплоту для адиабатного и политропного процессов (показатель политропы n = 1,1). Решение Для заданных условий молярная изобарная теплоемкость азота N2 составит: 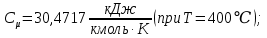 Массовая изобарная теплоемкость азота: 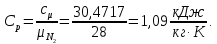 Изохорная теплоемкость определяется из уравнения Майера: 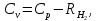 где газовая постоянная для азота 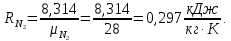 Тогда 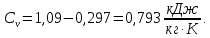 Определим параметры для адиабатного процесса Уравнение адиабатного процесса: 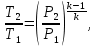 где k – показатель адиабаты: 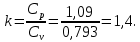 Значение температуры 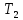 : :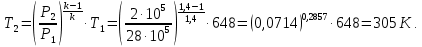 Изменение внутренней энергии газа: 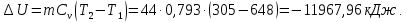 Работа расширения газа: 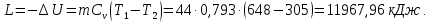 Подведенная теплота: 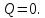 Определим параметры для политропного процесса Уравнение политропного процесса: 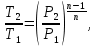 отсюда выразим температуру 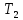 : :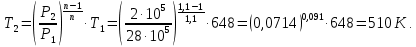 Изменение внутренней энергии газа: 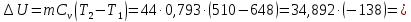 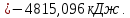 Работа расширения газа: 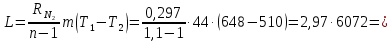 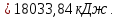 Подведенная теплота: 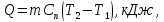 где 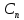 – политропная массовая теплоемкость газа: – политропная массовая теплоемкость газа: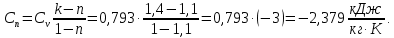 Тогда значение подведенной теплоты к газу: 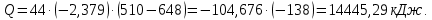 Ответ: для адиабатного процесса: 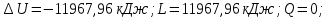 для политропного процесса: для политропного процесса: 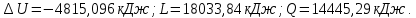 Контрольная задача №4 Построить и проанализировать произвольный цикл, который состоит из четырех произвольных последовательно осуществляемых следующих термодинамических процессов для сухого воздуха массой m = 1кг: 1-2 – изотермический (T = const); 2-3 – изобарный (p = const); 3-4 – изотермический (T = const); 4-1 – изобарный (p = const). В основных точках заданы следующие параметры: давление 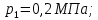 температура температура 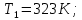 давление давление 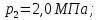 температура температура 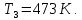 Принять удельную теплоемкость воздуха 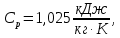 газовую постоянную газовую постоянную 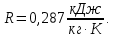 Требуется определить: давление, удельный объем и температуру для основных точек цикла (точек пересечения процессов); для каждого термодинамического процесса заданного цикла показатель политропы, теплоемкость, изменение внутренней энергии, энтальпи, энтропии, количество теплоты, работу; количество теплоты, подведенной и отведенной за цикл, работу цикла, термический КПД цикла; построить цикл в координатах 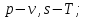 результаты расчета представить в форме таблицы. Решение: Так как процесс 1-2 является изотермическим, то температура в точках 1 и 2: 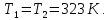 На основании уравнения Клапейрона можно определить удельный объем в точке 1: 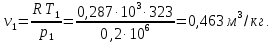 Удельный объем в точке 2: 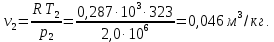 Так как процесс 2-3 является изобарным, то давление в точках 2 и 3: 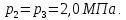 Удельный объем в точке 3: 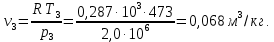 Так как процесс 3-4 является изотермическим, то температура в точках 3 и 4: 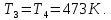 Так как процесс 4-1 является изобарным, то давление в точках 4 и 1: 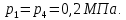 Удельный объем в точке 4: 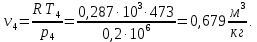 Определяем требуемые калорические параметры Процесс 1-2 (T = const): Изменение внутренней энергии: 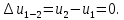 Изменение энтальпии: 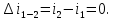 Изменение энтропии: 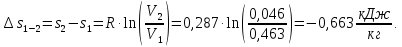 Работа: 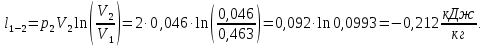 Количество теплоты: 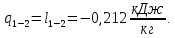 Процесс 2-3 (p = const): 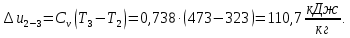 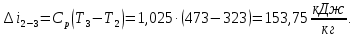 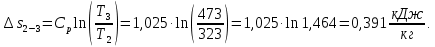 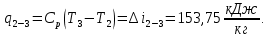 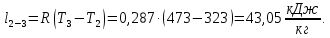 Процесс 3-4 (T = const): 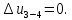 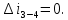 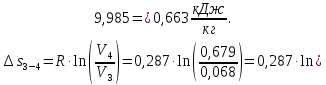 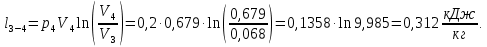 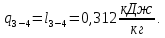 Процесс 4-1 (p = const) 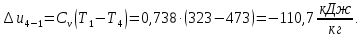 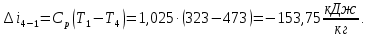 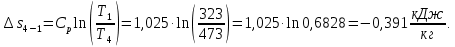 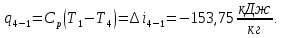 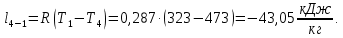 Полученные данные сводим в таблицу:
Количество теплоты, подведенное за цикл: 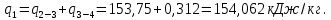 Количество теплоты, отведенное за цикл: 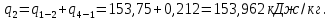 Термический КПД цикла: 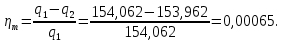 Работа цикла: 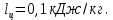
П 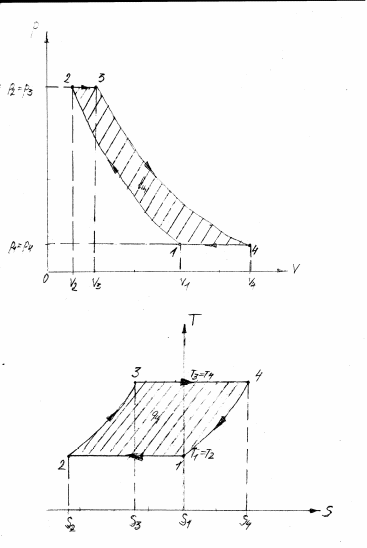 остроим графики цикла в координатах остроим графики цикла в координатах 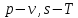 : : |