описание ОДР. Решение. Геометрическое представление исходных данных отображено на рис. 11

• Название: Решение. Геометрическое представление исходных данных отображено на рис. 11
• Анкор: описание ОДР
• Дата: 11.06.2021
• Размер: 71 Kb.
• Имя файла: Opisanie__ODR (1).doc
• Тип: Документы; #216718

Описание ОДР

Пример расчета попадания точки в заданную область.

Задана таблица работоспособности объекта.
Работоспособность объекта Таблица 1.2.

№ п/п	x1	x2	работоспособность объекта
1	6	10	Да
2	1	8	Да
3	2	3	Да
4	7	5	Да
5	8	2	Да
6	11	6	Да
7	10	8	Да

Вопрос: будет ли работоспособен объект с параметрами ?

Решение. Геометрическое представление исходных данных отображено на рис. 1.11.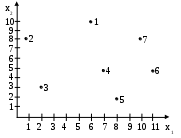




D


Рис. 1.11. Координаты исходных точек в ПДСК.

Из графического представления видно, что точка с координатами (6,6) попадает внутрь выпуклой области. Докажем этот факт аналитически, предварительно построив выпуклую область работоспособности заданного объекта.
Проведем построение области согласно алгоритму, изложенному в разделе 1.2.

1 шаг. Берется (N + 1) точки в N – мерном пространстве в нашем случае N=2, т.е.берем точки 1, 2, 3.

Через каждые N точек проводится гиперплоскость и заполняется таблица

Прямая	1 – 2	2 – 3	1 – 3
Вершина	3	1	2
координаты вершин	2; 3	6; 10	1; 8
координаты 1-ой точки	6; 10	1; 8	6; 10
координаты 2-ой точки	1; 8	2; 3	2; 3
уравнение прямой	x1 – 2,5x2 + 19 = 0	x1 + 0,2x2 – 2,6 = 0	7x1 - 4x2 – 2 = 0

2 шаг. Для точки 4 ищем генеральную гиперплоскость среди всех ранее построенных плоскостей. Является ли (1 – 2) генеральной гиперплоскостью для точки 4.

S (т.4) = 7 – 2,5  5 + 19 > 0

S (т.3) = 2 – 2,5  3 + 19 > 0, т.е. (1-2), не является для точки 4 генеральной гиперплоскостью.

Для т. 4 генеральная гиперплоскость (1-3);

S (т.4) = 7  7 – 4,5 - 2 > 0

S (т.2) = 7  1 – 4,8 - 2 < 0, т.е. (1-3), является для точки 4 генеральной гиперплоскостью.

Мы снова имеем (N + 1) точку – это 1, 3, 4

Через каждые N точек проведем гиперплоскости (в данном случае прямые)

Для упрощения построения часть таблицы не заполняется.

Прямая	1 – 3	3 – 4	1 – 4
Вершина	4	1	3

После обработки каждой точки генеральная гиперплоскость и плоскости повторяющиеся (одни и те же плоскости в разных таблицах) вычеркиваются.

3 шаг. Для точки 5 генеральная гиперплоскость (1 – 4)

Прямая	1 – 4	4 – 5	1 – 5
Вершина	5	1	4

а также (3 – 4)

Прямая	3 – 4	3 – 5	5 – 4
Вершина	5	4	3

4 шаг. Для точки 6 генеральная гиперплоскость (1 – 5)

Прямая	1 – 5	5 – 6	1 – 6
Вершина	6	1	5

5 шаг. Для точки 7 генеральная гиперплоскость (1 – 6)

Прямая	1 – 6	6 – 7	7 – 1
Вершина	7	1	6

Получили границу области работоспособности:

(1 – 2) – (2 – 3) – (3 – 5) – (5 – 6) – (6 – 7) – (7 – 1).

Окончательный шаг объекта для перехода от уравнений к неравенствам необходимо в линейную форму (левая часть равенства) поставить координаты вершины.

Если величина линейной формы положительна, то знак “=” заменяется на “”, если же отрицательна то знак “=” заменяется на “”.

Пример: (1 – 2): x₁ – 2,5x₂ + 19 = 0, S(т.3) = 2 – 2,5  3 + 19 > 0.

Соответствующее неравенство имеет вид: x₁ – 2,5x₂ + 19  0.

Аналогично получаем всю совокупность неравенств, которые описывают область работоспособности объекта.

(1 – 2) x₁ – 2,5x₂ + 19  0

(2 – 3) x₁ + 0,2x₂ – 2,6  0

(3 – 5) x₁ + 6x₂ - 20  0

(5 – 6)  -x₁ + 0,75x₂ + 6,5  0

(6 – 7)  -x₁ – 0,5x₂ +14  0

(7 – 1)  -x₁ - 2x₂ + 26  0

Полученная область представлена на рис. 1.12.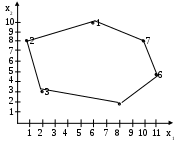



Рис. 1.12. Область решений системы неравенств.