Решение инженерных задач с помощью программ Excel и Mathcad». Решение инженерных задач с помощью программ Excel и Mathcad

• Название: Решение инженерных задач с помощью программ Excel и Mathcad
• Анкор: Решение инженерных задач с помощью программ Excel и Mathcad
• Дата: 26.12.2021
• Размер: 0.94 Mb.
• Имя файла: zapisko.doc
• Тип: Курсовая; #318568

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

БРЯНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Информатика и программное обеспечение»

КУРСОВАЯ РАБОТА

по курсу

«Информатика»

Тема: «Решение инженерных задач с помощью программ Excel и Mathcad»

Выполнил ст. гр. 16-КТО:

Резанов И.С.

Проверил:

БРЯНСК 2017

Содержание

Содержание 2

Введение 3

1. ЗАДАНИЕ №1 4

1.1. Условие задания 4

1.2. Решение 4

2. ЗАДАНИЕ №2 10

2.1. Условие задания 10

2.2. Решение 10

3. ЗАДАНИЕ №3 12

3.1. Условие задания 12

3.2. Решение 12

4. ЗАДАНИЕ №4 20

4.1. Условие задания 20

4.2. Решение 20

заключение 26

список используемой литературы 27

Введение

На дворе XI век – век компьютерных технологий. Компьютеры и все связанное с ними постоянно совершенствуются и все больше облегчает работу человека, в том числе при решение инженерных задач и при выполнение различных математических расчетов.

Часто при решение инженерных задач применяются традиционные языки программирования (BASIC[3], Pascal[4] и др.), а не электронные таблицы (Excel[2]) и специальные математические программы (Mathcad[1]), в связи с этим в данной курсовой работе основное внимание будет уделено использованию именно их.

Mathcad и Excel предназначены для решения схожих задач, поэтому рационально будет провести сравнение принципов работы этих пакетов программ при решении одних и тех же задач. Это позволит сделать выводы об использовании Mathcad и Excel, основанные на практических знаниях, и выяснить какая из них на сегодня является предпочтительней.

1. ЗАДАНИЕ №1

1.1. Условие задания

Дано нелинейное уравнение вида f(x)=0. Необходимо в программах Excel и Mathcad:

• 
  Построить график функции f(x) на заданном интервале. При построении графика в Excel использовать шаг табуляции h=0.2
  

• 
  Найти корни этого уравнения.
  
• 
  Найти экстремумы функции f(x).
  
• 
  Найти производную функции f(x) и построить ее график (выполняется только в Mathcad).
  
• 
  Сравнить полученные результаты и сделать выводы об эффективности Excel и Mathcad при решении таких задач.
  

Уравнение и интервал [-10; 5].

1.2. Решение

1. 
   Выполним табулирование функции в Excel на интервале [-10; 5] с шагом 0.2.
   
2. 
   На основе полученной таблицы табуляции строим график функции f(x) (рис 1.1).
   
3. 
   При таком построение мы получаем неверный график функции. Excel не определил наличие у графика функции наличия асимптот при х= 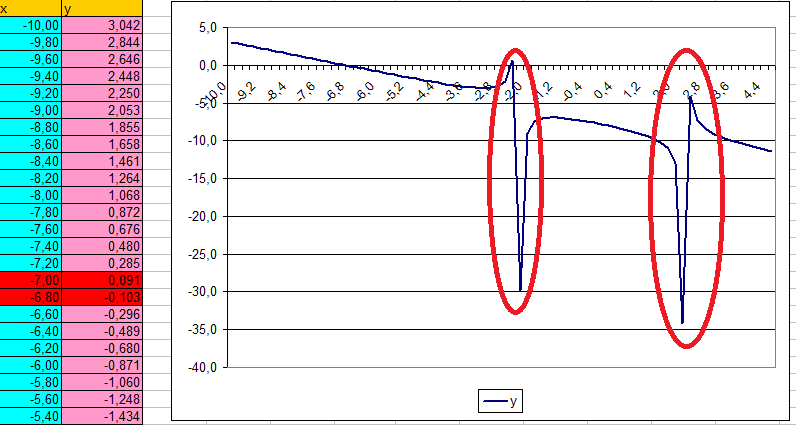(ошибка выделена на рис. 1.1). Для исправления ошибки исключим из таблицы значения аргумента равные , а добавим и построим заново график (рис. 1.2).
   

Рис. 1.1. Табуляция функции и построение графика в Excel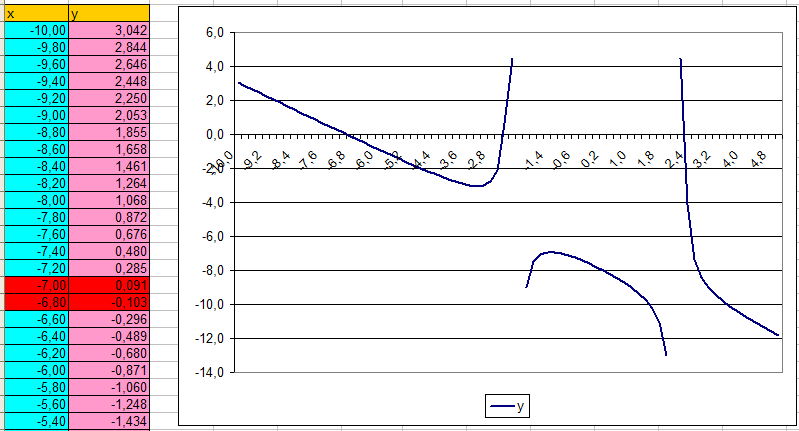


Рис. 1.2. Табуляция функции и построение графика в Excel после исправлений

4. 
   На полученном графике определяем приближенное значение корней уравнения. Данные корни будут находиться в точках пересечения графика функции с осью абсцисс, а также их приближенные значения можно определить по таблице табуляции в строках, где значения в столбце y меняют свой знак. Получаем следующие приближенные значения корней уравнения: -7; 2,4 и -2,4.
   
5. 
   С помощью процедуры подбор параметра определяем точное значение корня для каждого приближенного значения. Получаем значения корней представленные далее (рис. 1.3).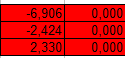
   

1.3. Фрагмент листа Excel с найденными корнями уравнения

6. 
   Найдем в Excel экстремумы функции f(x). По графику видно, что данная функция имеет только две точки экстремума (при х 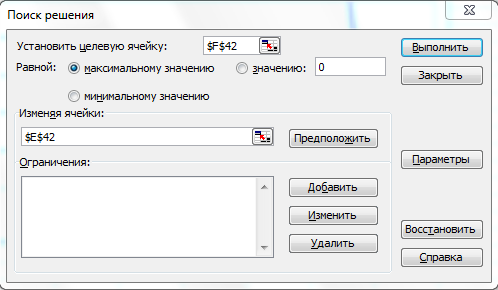[-3,6; -6] – минимума, а при х [-2; -0,4] – максимум). Для нахождения этого экстремума воспользуемся надстройкой «Поиск решений» и настроим ее согласно рис. 1.4. и рис. 1.5.
   

Рис. 1.4. Настройка формы «Поиск решений» для нахождения максимума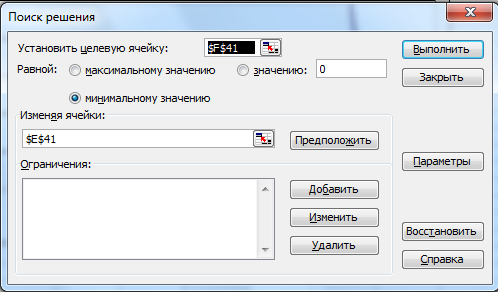



Рис. 1.5. Настройка формы «Поиск решений» для нахождения минимума

7. 
   Сформируем отчеты о результатах поисков (рис 1.6 и рис. 1.7), из которых видно, что искомые значения экстремумов функции x_макс=-1,32; x_мин=-3,17.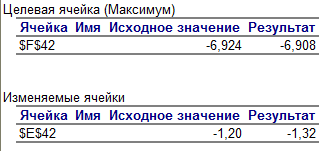
   

Рис. 1.6. Отчет о результатах поиска максимума функции с помощью надстройки «Поиск решений»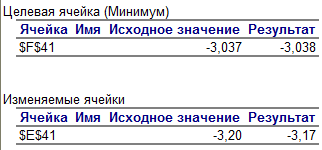


Рис. 1.7. Отчет о результатах поиска минимума функции с помощью надстройки «Поиск решений»

8. 
   С помощью программы Mathcad построим график функции 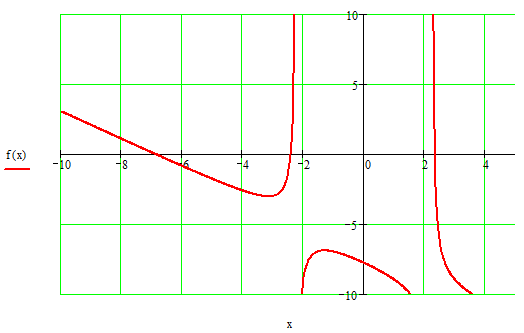на интервале [-10; 5] (рис. 1.8.). По графику определяем приближенные значения корней уравнения: -7, -2,5 и 2,4.
   

Рис. 1.8. График функции f(x), построенный в Mathcad

9. 
   С помощью функции root находим точные значения корней уравнения: x₁ =-2,33; x₂ =-2,424; x₃ =-6,906.
   
10. 
    Используя символьные вычисления Mathcad, найдем производную: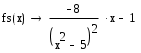
    

11. 
    Построим график производной функции f(x). По графику определяем приближенное значение корней 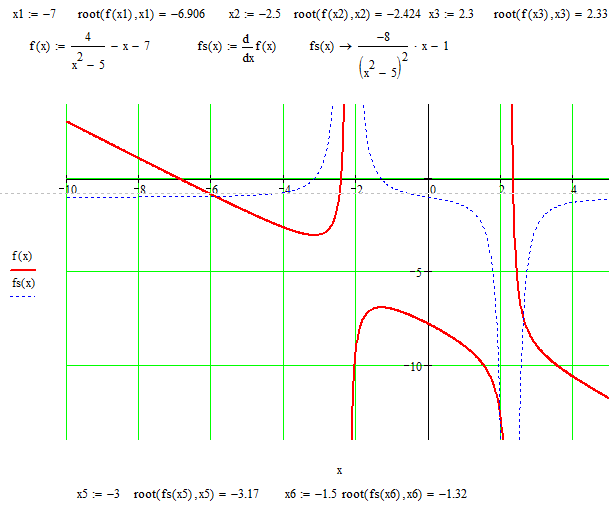: x₁=-3; x₂=-1,5. С помощью функции root находим точное значение корня уравнения (рис. 1.9), а значит и значение экстремума f(x): x_макс=-1,32; x_мин=-3,17.
    

Рис. 1.9. Нахождение корней уравнения и экстремума функции с помощью Mathcad
Выполнив данное задание, можно заметить ряд явных преимуществ Mathcad над Excel, таких как построение в одной системе координат графиков нескольких функций, а также нахождение производных.

2. ЗАДАНИЕ №2

2.1. Условие задания

Даны матрицы A, B, и С. Вычислить матрицу D по формуле. Используя коэффициенты полученной матрицы D решить систему уравнений.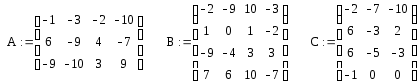





Система уравнений: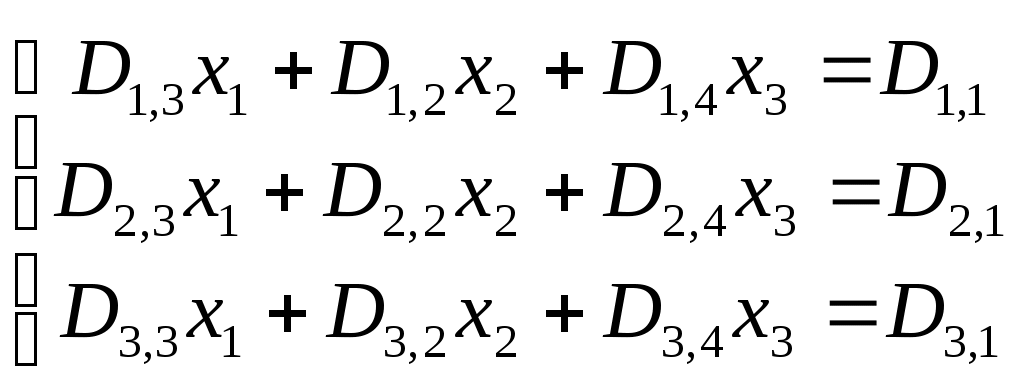

2.2. Решение

1. 
   С помощью Excel произведем расчеты матрицы D (рис. 2.1).
   

Рис. 2.1. Вычисление матрицы D в Excel

2. 
   Запишем систему уравнений, используя коэффициенты из полученной матрицы: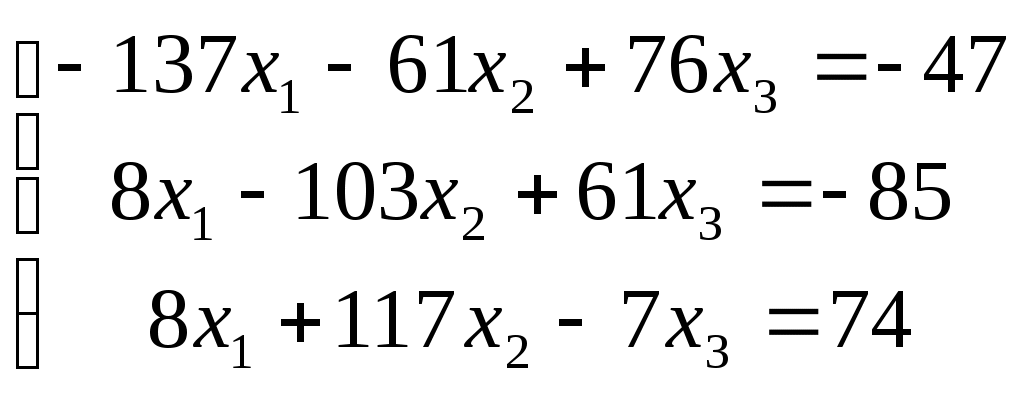
   

3. 
   Решим полученную систему уравнений в Excel с помощью обратной матрицы (рис. 2.2). В результате получим вектор решения: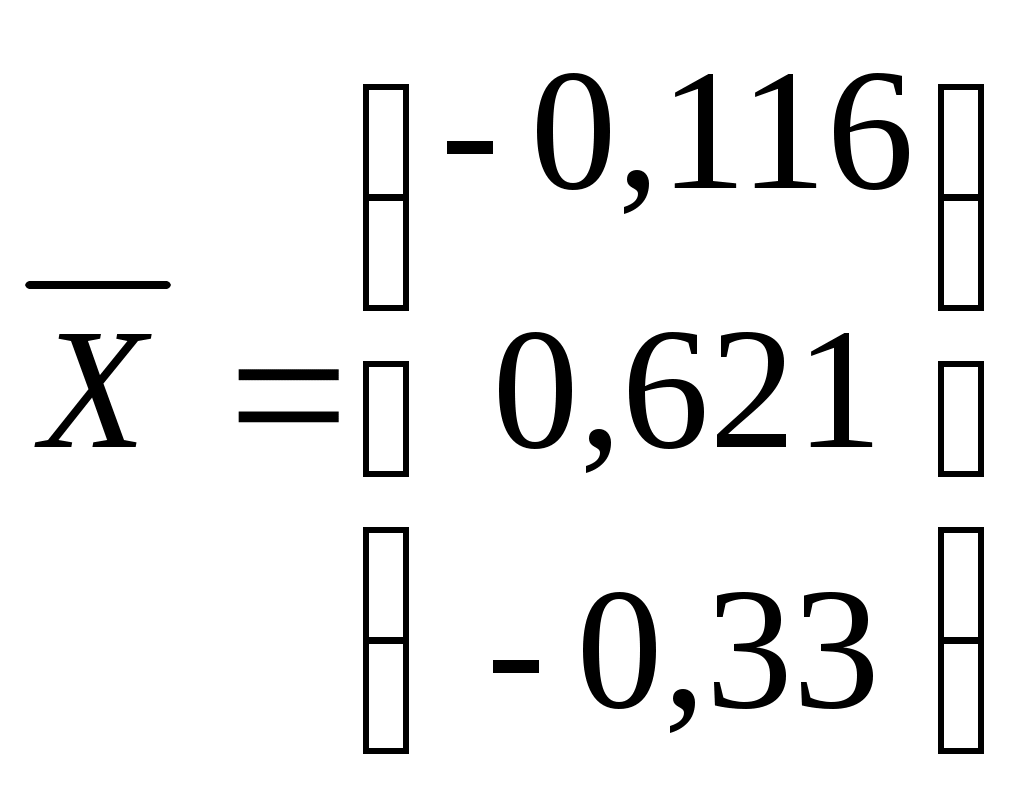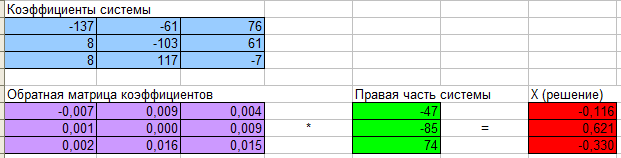
   

Рис. 2.2. Решение системы линейных уравнений с помощью Excel

4. 
   Проведем расчет матрицы D средствами Mathcad. Заполним матрицу коэффициентов системы уравнений и найдем ее решение (рис. 2.3).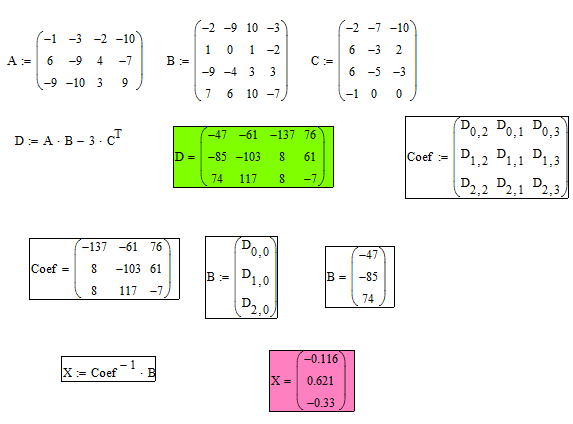
   

Рис. 2.3. Вычисление матрицы D и нахождение решения системы уравнений в Mathcad

3. ЗАДАНИЕ №3

3.1. Условие задания

Даны координаты точек (x_i,y_i), для которых необходимо:

• 
  Провести кусочно-линейную интерполяцию и найти значения y для следующих значений x: 1.3, 2.6, 4.4, 5.9, 7.1, 8.75. Построить график.
  
• 
  Провести полиномиальную интерполяцию и найти значения y для следующих значений x: 1.3, 2.6, 4.4, 5.9, 7.1, 8.75. Построить график. Записать уравнение полинома (коэффициенты полинома указать с точностью 7 знаков после запятой)
  
• 
  Провести 2 вида аппроксимации согласно варианту. Построить оба графика на одной координатной плоскости. В обоих случаях определить сумму квадратов отклонений для узловых точек. Данное задание выполнить как в Excel, так и в Mathcad.
  

Таблица 1

Узловые точки

x	0	1	2	3	4	5	6	7	8	9
y	-31,57	5,51	-25,71	10,47	8,46	-0,56	24,07	12,04	30,45	7,6

Виды аппроксимации:

• 
  Полином 4-ой степени;
  
• 
  Полином 6-ой степени.
  

3.2. Решение

1. 
   Проведем кусочно-линейную интерполяцию (интерполяция – определение наиболее правдоподобных промежуточных значений в интервале между известными значениями (подбор гладкой кривой, проходящей через заданные точки или максимально близко к ним)) для заданных точек (x_i,y_i) и определяем значение функции для указанных значений аргумента (рис. 3.1). Результат представлен в таблице 2.
   

Таблица 2

Значения функции для указанных значений аргумента при кусочно-линейной интерполяции

x	1.3	2.6	4.4	5.9	7.1	8.75
y	3.856	-4.002	4.852	21.607	13.881	13.313

Для решения данной задачи использовалась функция linterp(X, Y, xx), которая осуществляет кусочно-линейную интерполяцию. Аргументами этой функции являются два вектора X и Y, содержащие исходные данные и независимая переменная xx.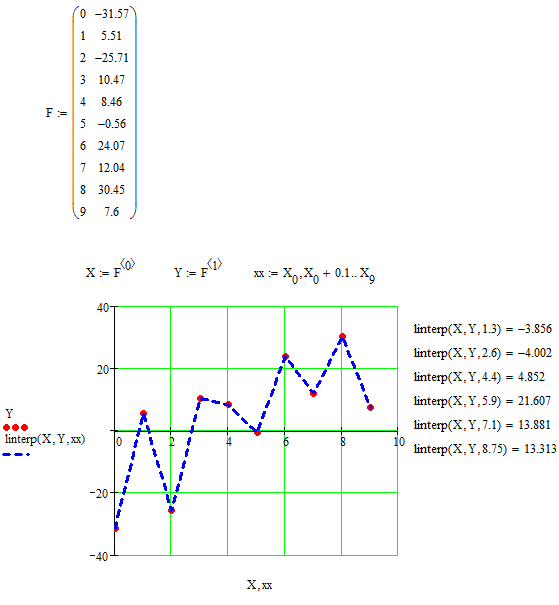


Рис. 3.1. Кусочно-линейная интерполяция в Mathcad

2. 
   Проведем полиномиальную интерполяцию. Учитывая, что задано 10 точек, то полином должен быть 9-й степени.
   

В результате получили полином: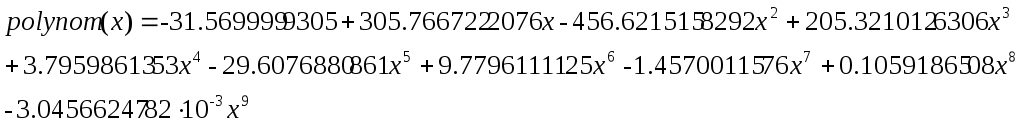



Построим его график, на котором отметим исходные точки. По графику можно убедиться, что полином проходит через все заданные точки. С помощью полученного полинома определим для заданных точек значения функции (рис. 3.2). Найденные значения представлены в таблице 3.

Таблица 3

Значения функции для указанных значений аргумента при полиноминальной интерполяции

x	1.3	2.6	4.4	5.9	7.1	8.75
y	-14.869	-3.458	0.779	21.923	8.642	96.351

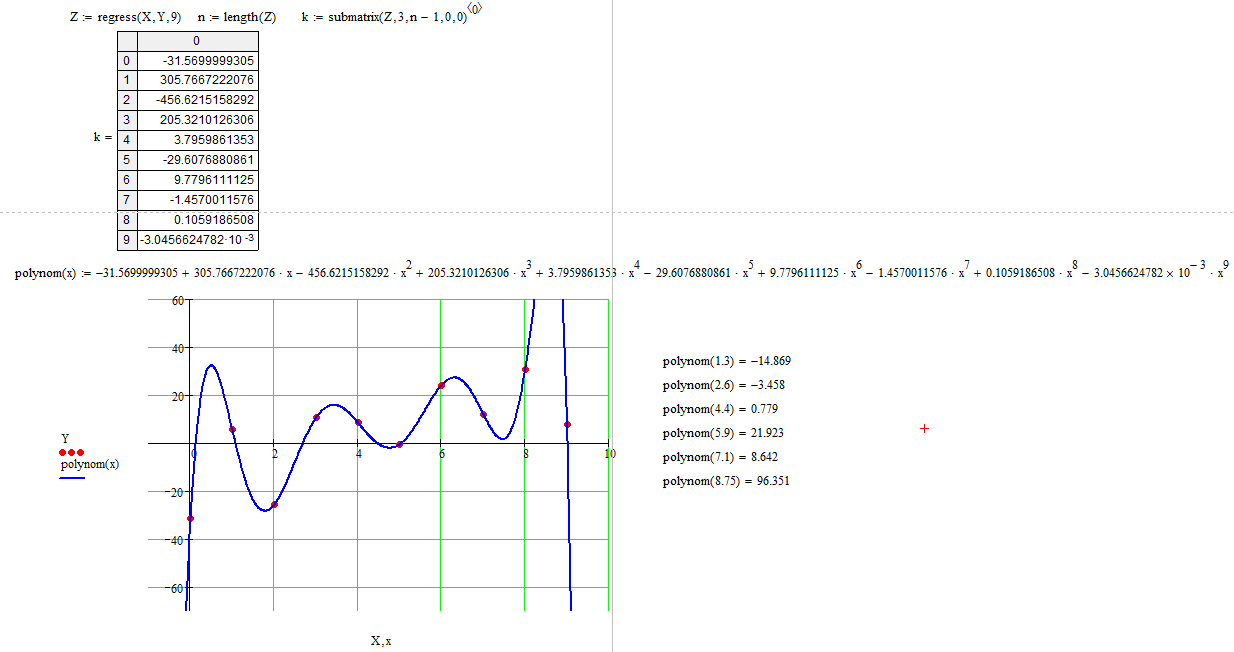Рис. 3.2. Полиномиальная интерполяция в Mathcad

При решение данной поставленной задачи мы воспользовались рядом функций: regress, length, submatrix.

regress(х, у, k) — возвращает вектор коэффициентов для построения полиномиальной регрессии данных (зависимость одной переменной от другой).

• 
  x — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
  

• 
  у — вектор действительных данных значений того же размера;
  

• 
  k — степень полинома регрессии (целое положительное число);
  

length(Z) – количество элементов в векторе Z.

submatrix(A, ir, jr, ic, jc) – подматрица, состоящая из всех элементов, содержащихся в строках с ir по jr и столбцах с ic по jc матрицы А.

3. 
   Проведем с помощью Mathcad аппроксимацию (Аппроксимация – поиск функции, которая с заданной степенью точности описывает исходные данные) для заданных точек с помощью линейной и степенной функций. Определим сумму квадратов отклонений для узловых точек (рис. 3.3):
   
   • 
     Для полинома 4-ой степени эта величина равна 1,228*10³.
     
   • 
     Для полинома 6-ой степени эта величина равна 906,989.
     

Можно сделать вывод, что с помощью полинома 6-ой степени можно получить более точное приближение.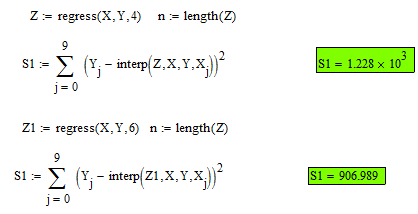


Рис. 3.3. Аппроксимация точек в Mathcad

3. 
   Построим графики аппроксимирующих функций: полинома 4-ой (рис. 3.4) и 6-ой (рис. 3.5) степеней.
   
4. 
   Проведем аппроксимацию точек с помощью Excel. Для этого сначала заполним исходную таблицу точек и отметим эти точки на координатной плоскости (рис. 3.6).
   
5. 
   Вызовем контекстное меню для одной из точек на графики и выберем пункт «Добавить линию тренда…». Для начала проведем аппроксимацию с помощью полинома 6-ой степени. Для этого в открывшемся диалоговом окне «Линия тренда» выберем «полиноминальная» и выберем степень «6» (рис. 3.7).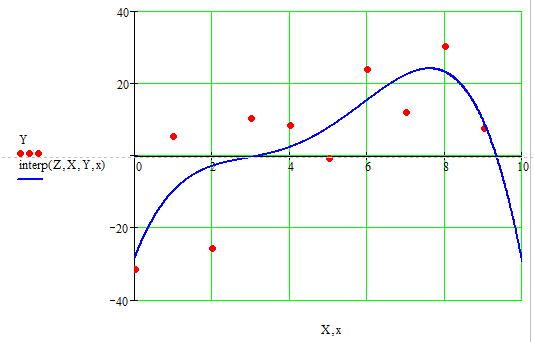
   

Рис. 3.4. График аппроксимации с помощью полинома 4-ой степени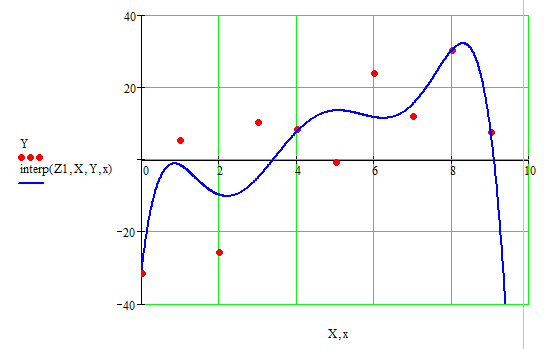


Рис. 3.5. График аппроксимации с помощью полинома 6-ой степени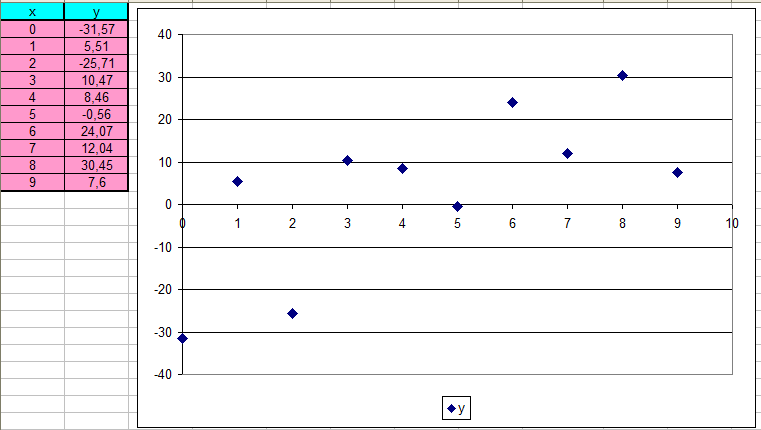



Рис. 3.6. Исходные точки для аппроксимации на координатной плоскости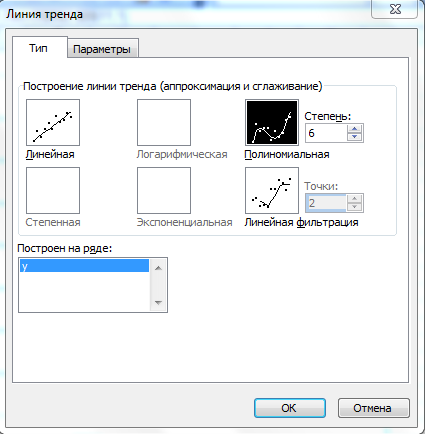


Рис. 3.7. Добавление на график аппроксимирующей линии (линии тренда)

3. 
   Аналогично добавляем линию тренда для полинома 4-ой степени. В настройках линии тренда выставим галочку «показать уравнение на диаграмме». Результат представлен на рис. 3.8 и 3.9. Получили следующие аппроксимирующие функции:
   
   • 
     Для полинома 6-ой степени:
     

y = -0,031953x⁶ + 0,865191x⁵ - 8,892620x⁴ + 42,972152x³ - 97,182284x² + 91,113205x - 30,372927

• 
  Для полинома 4-ой степени:
  

y = -0,108446x⁴ + 1,886240x³ - 10,797746x² + 27,613821x - 28,134580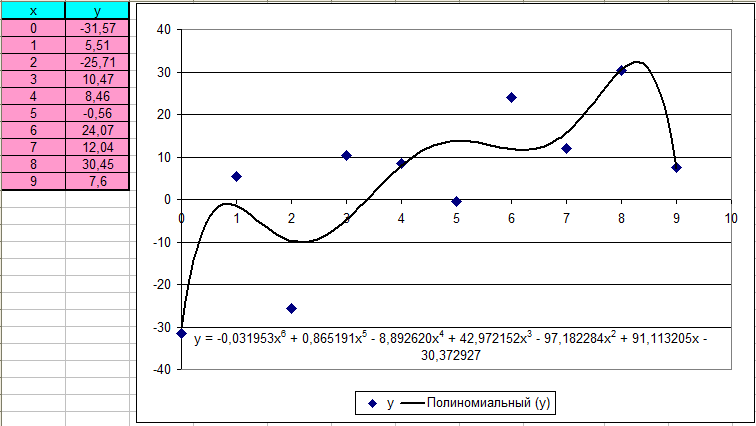


Рис. 3.8. График аппроксимации с помощью полинома 6-ой степени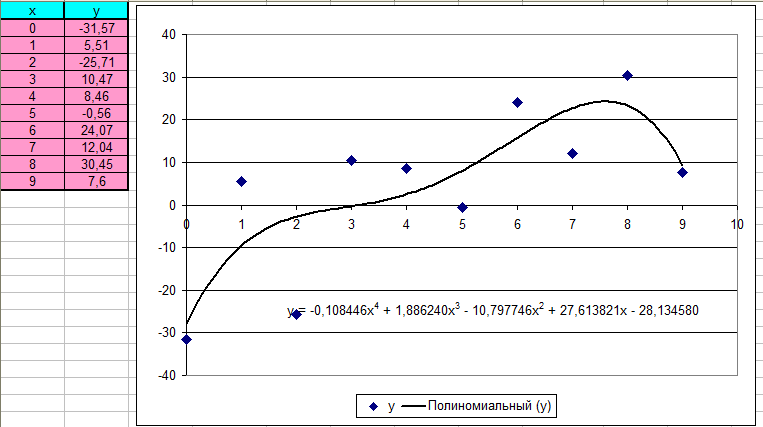



Рис. 3.9. График аппроксимации с помощью полинома 4-ой степени

3. 
   Определим сумму квадратов отклонений для полученных функций в узловых точках (рис.3.10). Получим:
   
   • 
     Для полинома 4-ой степени эта величина равна 1228,243.
     
   • 
     Для полинома 6-ой степени эта величина равна 907,065.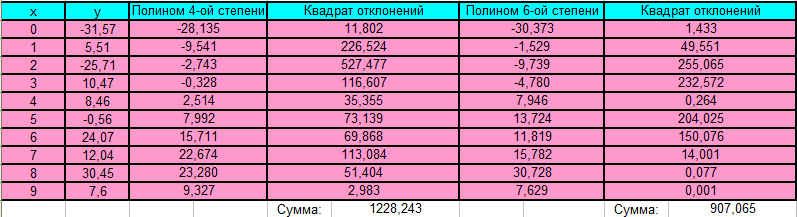
     

Рис. 3.10. Расчет в Excel суммы квадратов отклонений для аппроксимирующих функций

4. ЗАДАНИЕ №4

4.1. Условие задания

Найти экстремум функции двух переменных согласно варианту в Excel и Mathcad. Построить график двухмерной поверхности в Excel и Mathcad. Сравнить результаты и сделать выводы.

4.2. Решение

1. 
   Построим график функции в Mathcad (рис.4.1).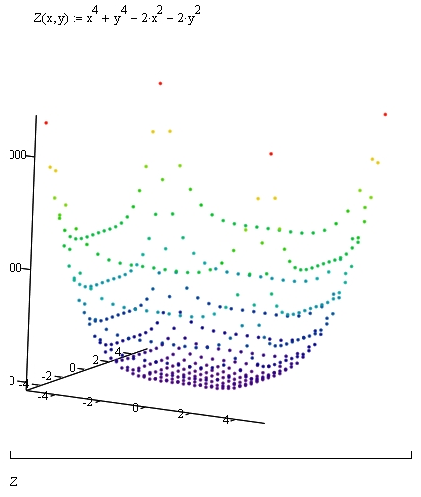
   

Рис. 4.1. Построение поверхности в Mathcad

2. 
   По графику видим, что функция z имеет целую область экстремумов, напоминающую квадрат, в которой имеется целый ряд перегибов поверхности.
   
3. 
   Для нахождения экстремумов данной функции необходимо вычислить частные производные и . Затем, используя определенные по графику координаты точек перегиба, решим систему уравнений, в которой найденные ранее частные производные 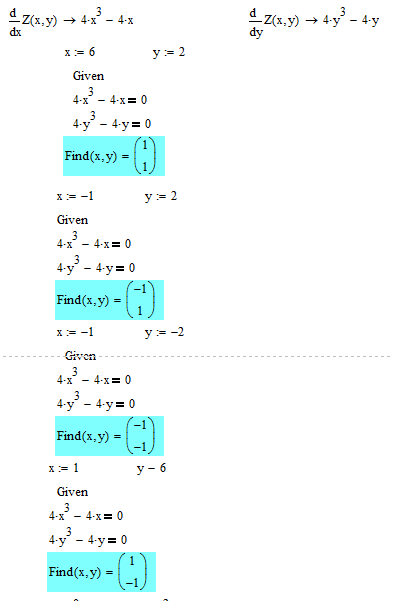равны 0. Решение этих систем являются координатами точек перегиба графика функции. Результаты представлены на рис. 4.2 и рис 4.3
   

Рис. 4.2 Нахождение экстремумов функции в Mathcad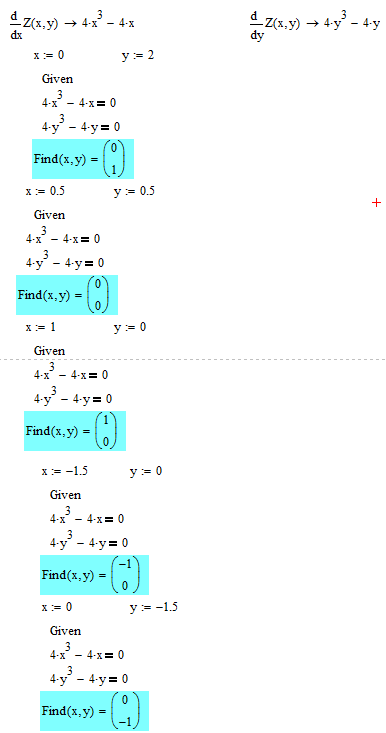



Рис. 4.3 Нахождение экстремумов функции в Mathcad

4. 
   Теперь выполним это же задание в Excel. Для этого сначала проведем табуляцию функции на интервале по х 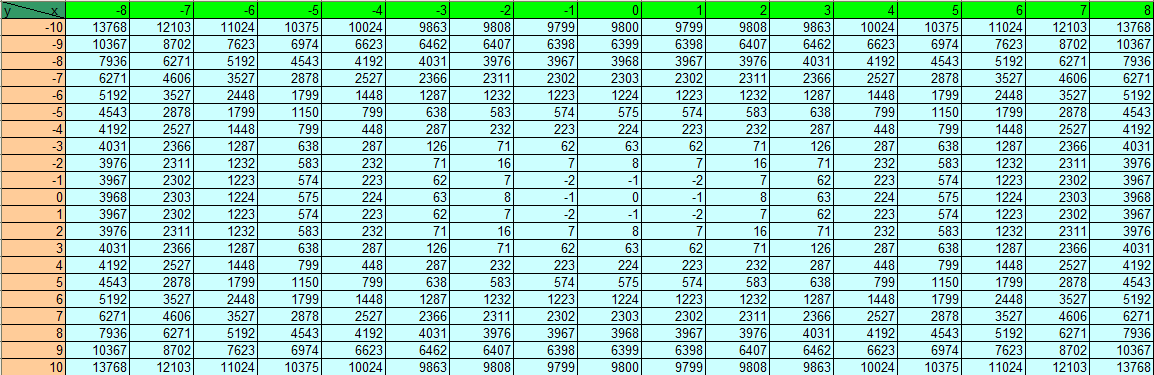[-8;8] и y [-10;10] (рис. 4.4).
   

Рис. 4.4. Табуляция функции двух переменных в Excel

5. 
   На основе полученной таблицы строим поверхность (рис. 4.5).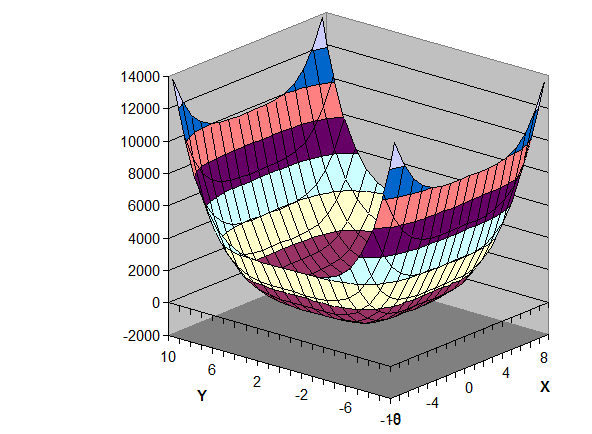
   

Рис. 4.5. График функции двух переменных в Excel

6. 
   С помощью надстройки «Поиск решения» найдем точки экстремумов. Для нахождения минимумов настроим соответствующие диалоговые окна аналогично рис. 4.6, а для максимума – рис. 4.7. В результате выполнения получим искомые точки (рис. 4.8).
   

Рис. 4.6. Настройка формы «Поиск решения» для нахождения минимума функции двух переменных


Рис. 4.7. Настройка формы «Поиск решения» для нахождения максимума функции двух переменных


Рис. 4.8. Координаты искомых экстремумов

6. 
   Искомые значения экстремумов функции двух переменных можно также увидеть в отчетах по результатам поиска, сформированным в ходе поиска. В качестве примера приведём один из четырех отчетов поиска минимума и отчет по поиску максимума (рис. 4.9 и рис 4.10).
   

Рис. 4.9. Отчет о результатах поиска минимума функции двух переменных с помощью надстройки «Поиск решений»


Рис. 4.10. Отчет о результатах поиска максимума функции двух переменных с помощью надстройки «Поиск решений»

6. 
   Однако в Excel проблематично найти часть экстремумов. По графику видно, что в части экстремумов график по x принимает максимальное значение, а по y – минимальное. В результате этого, их через «Поиск решения» не удастся, так как благодаря «Поиску решения» можно найти максимум (минимум) функции двух переменных, только в том случае, когда обе переменные принимают в одной точке либо максимальное значение, либо минимальное.
   

заключение

Технология работы в средах Excel и Mathcad имеет много общего. Но поработав в этих программных средах, можно прийти к выводу о преимуществе Mathcad над Excel при решение математических задач.

Mathcad является более продуманной системой, в частности этом пакете имеется возможность нахождения производных и построение нескольких графиков функций в одной системе координат и др. Бесконечноe количество адресов ячеек, которые приходится записывать при вводе формул, в Excel является одним из минус этого пакета. Ведь в случае ошибки в записи формулы найти ее будет крайне трудно. В то время как в Mathcad прозрачный и простой пользовательский интерфейс и он действительно позволяет пользователю решать задачи именно на том языке, которому его учили в школе и институте, а не заставляет выучивать новый, свой собственный.

Проделанная работа в ходе выполнения работы позволила сформировать более четкое представление о Mathcad и Excel, о их плюсах и минусах, закрепить и развить навыки по данным программным продуктам.

список используемой литературы

1. 
   Кирьянов, Д. В. Mathcad 14/ Д. В. Кирьянов. – СПб.: BHV, 2007. – 704с.
   

2. 
   Веденеева, Е. А. Функции и формулы Excel 2007. Библиотека пользователя/ Е. А. Веденеева. — СПб.: Питер, 2008. – 384с.
   
3. 
   Курилович, В. Информатика. Языки Basic/ В. Курилович. – М.: СОЛОН-Пресс, 2005. – 224с.
   
4. 
   Ушаков, Д. М. Паскаль для школьников/ Д. М. Ушаков, Т. А. Юркова. – СПб.: Питер, 2005. – 256с.