проект. ПЗ 19 Решение иррациональных неравенств (1). Решение иррациональных неравенств
 Скачать 26.4 Kb. Скачать 26.4 Kb.
|
|
Практическая работа «Решение иррациональных неравенств» Цель работы: Обобщить и систематизировать знания по теме «рациональные и иррациональные неравенства». Совершенствовать умения и навыки решения рациональных и иррациональных неравенств Теоретические сведения к практической работе: Свойства числовых неравенств. 1. Если а > b , то b < а; наоборот, если а < b, то b > а. 2. Если а > b и b > c, то а > c. Точно так же, если а < b и b < c, то а < c. 3. Если а > b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е. к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же величину. 4. Если а > b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать. Замечание. Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным 5. Если а > b и c < d, то а – c > b – d; если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак того неравенства, из которого вычиталось другое. 6. Если а > b и m – положительное число, то m а > m b и 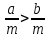 , , т.е. обе части неравенства можно умножить или разделить на одно и то же положительное число (знак неравенства остаётся тем же). Если же а > b и n – отрицательное число, то n а < n b и 7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать. Следствие. Если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2, т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат. 8. Если а > b, где а, b > 0, то Опр. Иррациональными неравенствами называются, в которых переменные или рациональные функции переменных находятся под знаками корней. При решении таких неравенств используют следующее утверждение: если обе части принимают только неотрицательные значения, то возведя обе части неравенства в квадрат, сохранив знак исходного неравенства, получим неравенство равносильное данному. Задания для самостоятельного решения: Вариант 1. А) 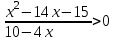 б) б)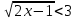 в) в) Вариант 2 А) 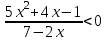 б) б) 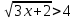 в) в)Контрольные вопросы: Каковы свойства числовых неравенств? Какие неравенства являются иррациональными? В чем заключаются особенности решения иррациональных неравенств? |
