асэм контрольная. КОНТРОЛЬНАЯ ГАЙДИС. Решение Исходная таблица состояний Sj S0
 Скачать 256.8 Kb. Скачать 256.8 Kb.
|
1 2 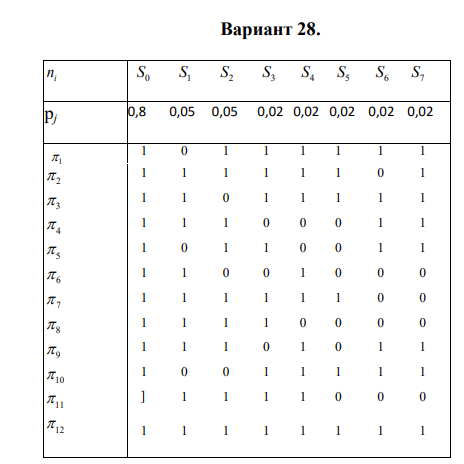 Курсанты, которые выполняют варианты 27-38 должны: 1) произвести минимизацию теста информационным методом; 2) по полученной минимизированной таблице состояний построить дерево безусловного алгоритма поиска места отказа. Минимизация теста информационным способом Решение Таблица 1 Исходная таблица состояний
Количество информации, которое несет i-я проверка о состоянии объекта диагностирования на первом шаге отбора: 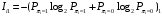 , (1) , (1)где цифра в индексах левой и правой частей уравнения обозначает номер шага; 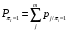 - вероятность того, что объект находится в тех m-состояниях из их общего числа N, для которых результатi-й проверки равен 1; - вероятность того, что объект находится в тех m-состояниях из их общего числа N, для которых результатi-й проверки равен 1;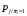 - вероятность нахождения объекта в состоянии Sj, для которого проверке - вероятность нахождения объекта в состоянии Sj, для которого проверке 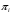 соответствует 1; соответствует 1;m-число состояний, для которых проверка 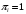 ; ;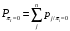 - вероятность того, что объект находится в тех n-состояниях, для которыхi-я проверка равна 0; - вероятность того, что объект находится в тех n-состояниях, для которыхi-я проверка равна 0;n-число состояний, для которых 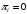 ; ;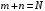 (Для рассматриваемого случая N=8). (Для рассматриваемого случая N=8).Сумма всех вероятностей для каждого 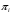 : :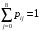 . .В соответствии с этими зависимостями для отбора первой проверки в тест найдем суммы вероятностей тех состояний, для которых 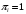 , и суммы вероятностей тех состояний, для которых , и суммы вероятностей тех состояний, для которых 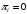 . .Так для π1: 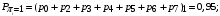 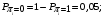 Для π2: 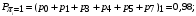 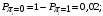 Для π3: 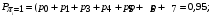 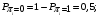 Для π4: 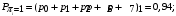 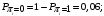 Для π5: 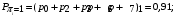 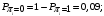 Для π6: 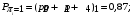 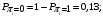 Для π7: 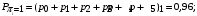 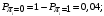 Для π8: 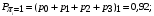 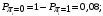 Для π9: 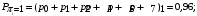 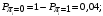 Для π10: 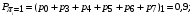 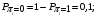 Для π11: 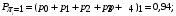 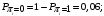 Для π12: 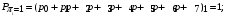 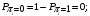 Количество информации, которое несет 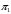 на первом шаге подсчитывается по формуле (1): на первом шаге подсчитывается по формуле (1):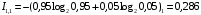 ; ;Для π2: 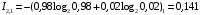 ; ;Для π3: 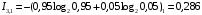 ; ;Для π4: 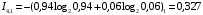 ; ;Для π5: 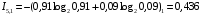 ; ;Для π6: 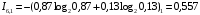 ; ;Для π7: 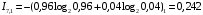 ; ;Для π8: 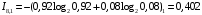 ; ;Для π9: 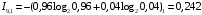 ; ;Для π10: 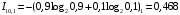 ; ;Для π11: 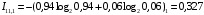 ; ;Для π12: 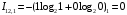 ; ;Эти данные записаны в последней колонке табл. 1. В тест отбирается проверка π6, как дающая максимум информации. По этой проверке табл. 1 делится на две части L1 и L2, представленные в табл. 2. Для отбора следующей проверки (второй шаг) используется формула 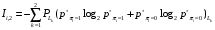 , (2) , (2)где 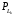 - вероятность того, что состояние объекта попало в часть Lkтабл. 2. Она равна сумме вероятностей тех состояний, которые вошли в данную часть таблицы: - вероятность того, что состояние объекта попало в часть Lkтабл. 2. Она равна сумме вероятностей тех состояний, которые вошли в данную часть таблицы: 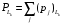 . .Для табл. 2 получаем 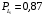 ; ;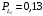 . .Таблица 2 Результат первого шага минимизации
Условные вероятности 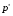 того, что проверка принимает значение 1 или 0 соответственно при условии, что состояние находится в Lk-й части таблицы: того, что проверка принимает значение 1 или 0 соответственно при условии, что состояние находится в Lk-й части таблицы: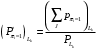 ; ; 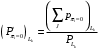 . .Для π1 имеем: 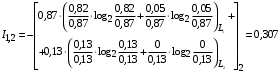 Для π2: 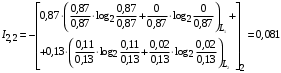 Для π3: 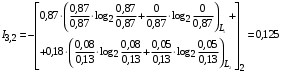 Для π4: 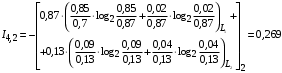 Для π5: 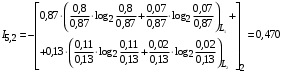 Для π7: 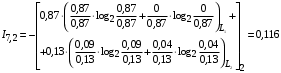 Для π8: 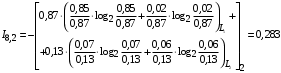 Для π9: 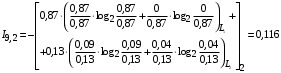 Для π10: 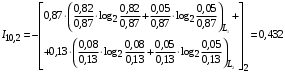 Для π11: 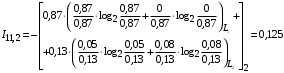 Для π12: 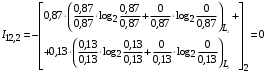 Производя подобные вычисления, заполняем столбец Ii2 в табл. 2. В тест по максимальному значению выбирается π5, разбивающий каждую часть табл. 2 на две части. В результате получается табл. 3, состоящая из четырех частей L1..L4. Строка проверки π4 поставлена первой. Здесь оказывается уже выделенным состояние S0, S4, из которого состоит часть L1. Отбор следующей проверки в тест (третий шаг) производится по табл. 3 с использованием формулы 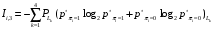 , (3) , (3)где 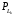 , ,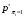 и и 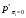 имеют смысл: имеют смысл: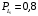 2; 2;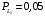 ; ;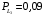 ; ;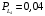 . .Если в какой-то части Lkтаблицы проверке πi соответствует только единицы или только нули, то для этой части информация равна 0. 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
