ОФВ Задачи. ОФВ до пасхи. Решение Используем формулу для определения наращенной суммы (простые проценты) s n S
 Скачать 151.45 Kb. Скачать 151.45 Kb.
|
|
Вариант № 6 1. Ссуда 350000 руб. выдана на 4 года под 23% годовых (простые проценты). Во сколько раз больше наращенная сумма по сравнению со ссудой? Решение Используем формулу для определения наращенной суммы (простые проценты): Sn = S0 *(1+ i *n) S0 – сумма ссуды; Sn – наращенная сумма; i – годовая ставка; n – число лет. Подставляем: Sn =350000*(1+ 0,23*4) =672 000 руб. Увеличение составит 672000/350000= 1,92 раза. 2. Номинальная процентная ставка составляет 12% годовых при годовом темпе инфляции 4%. Чему равна годовая ставка с учётом инфляции? Чему равна эффективная реальная процентная ставка, если проценты начисляются ежемесячно? ежедневно? ежеквартально? Решение Дано: i = 12% = 0,12, h = 4% = 0,04 Найти: r, i Реальную годовую ставку с учетом инфляции определим по формуле: 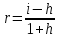 где i - номинальная процентная ставка; h - темп инфляции 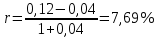 Эффективная процентная ставка вычисляется по простой формуле: r = (1 + i/n)^n - 1. Ежемесячно r = (1+0,0769/12)^12 - 1 = 7,967% ежедневно = (1+0,0769/365)^365 – 1 = 7,993% ежеквартально = (1+0,0769/4)^4 – 1 = 7,915% 3. Клиент поместил в банк вклад в сумме 1800000 руб. под 8% годовых с ежемесячной выплатой процентов. Какую сумму клиент будет получать каждый месяц, если начисление производится по формуле простых процентов? Решение P= 1800 000 r=0,08 n=1/4 1) F=P(1+nr)=1800000*(1+0,08/4)= 1836000 I=1836000-1800000=36 000 руб 2) F=1800000*(1+(1/12)*0,08)= 1812000 I=1 812 000 4. Месячный темп инфляции составляет 2%. Найти индекс цен и темп инфляции за год, определить реальную наращенную сумму с учётом инфляции, если на сумму 1500000 руб. в течение года начислялась простая процентная ставка 15% годовых (К=360). Решение Темп инфляции за год равен: а=(1+0,02)^12–1= 26,82% Индекс цен= 1,26 Наращенная сумма равна 1500000*1,15=1 725 000 руб В случае сложных процентов месячная ставка равна (1+0,15)^(1/12)-1 = 1,17% Или 1,17%. Годовая ставка, при которой потери из-за инфляции равны наращению составит 26,82 % 5. Фонд создается в течение 10 лет. Средства поступают в фонд в конце года равными суммами. На собранные средства в конце года начисляется 10% годовых. На сколько процентов возрастет наращенная сумма фонда при переходе к взносам в конце каждого квартала? Ответ привести с точностью до 0,01%. Решение Определим коэффициент наращения для каждого способа начисления процентов по формуле: r = [(1 + j/m)^(n*m) - 1]/[(1 + j/m)^(m) – 1] = где j – номинальная процентная ставка ренты , m и p число периодов начисления процентов и платежей в году, n – число лет. r =((1 + 0,1/4)^(10*4) - 1)/((1 + 0,1/4)^(4) - 1)= 16,2317399 ответ 16,23 % 6. Найти срок ренты постнумерандо, если наращенная сумма равна 5000; процентная ставка равна 10%; рентный платёж равен 1000. Решение 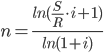 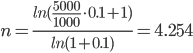 7. Какую сумму нужно положить в банк под 10% годовых мужчине 52 лет, чтобы по достижении им пенсионного возраста 60 лет в течение 15 лет в начале каждого месяца снимать по 10000 рублей, если проценты капитализируются в конце каждого месяца? Решение R – сумму, нужную положить в банк S – наращенная сумма по достижении им пенсионного возраста 60 лет. А = S Капитализация в конце месяца: А = 10 000*(1-(1+0,10/12)^(–15*12) )*(1+0,10/12)^ (12/12)/((1+0,10/12)^(12/12) –1) = 938 329,17 S = R*(1 + 0,1/12)^(60– 52)*12 = R*(1 + 0,01)^96 = 2,60 R = S/(1+0,01)^96 = S/2,60 = 938329,17/ 2,60 = 360 996,79 Ответ 360 996,79 8. Рыночная цена 10-ти процентной облигации номиналом 2000 руб. за три года до погашения равна 2500 руб. найти текущую стоимость облигации при процентной ставке 9% и её курс. Решение Дано: С = 10% = 0,1, N = 2000 руб., n = 3 года, V = 2500 руб., г = 9% Найти: К, Р Найдем курс по формуле: К = V/N = 2500/ 2000 = 125 % Текущая стоимость Р вычисляется по формуле: 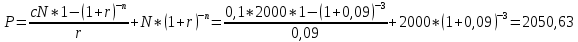 Ответ К= 125%, Р= 360 996,79 9. Заемщик должен уплатить 80000 руб. через 75 дней. Кредит выдан под 29% годовых (простые проценты). Какова первоначальная сумма долга и дисконт (К=360)? Решение  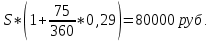 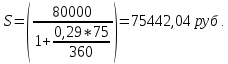 Дисконт равен D = 80000 – 75442,04 = 4557,96 ОТВЕТ: S = 75442.04 руб., D = 4557,96 руб. 10. В банк положен депозит в размере 2400 руб. под 7% годовых по схеме сложных процентов. Найти величину депозита через три года при начислении процентов 4 раз в году. Решение 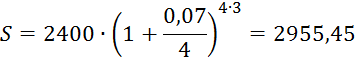 Ответ 2995,45 11. Портфель состоит из двух ценных бумаг A и B, ожидаемая доходность и риск которых, выраженные в процентах, равны A(7,19), B(12,24). Коэффициент корреляции бумаг равен 1. Найти множество допустимых портфелей, построить график. Определить доходность портфеля минимального риска. Решение Риск портфеля, состоящий из двух активов, рассчитывается по формуле:  Таким образом, целевая функция σp → min При следующих ограничениях: — по составу портфеля θa + θb = 1, — удельные веса не должны быть отрицательны. 1. Определяем доходность портфеля минимального риска. В случае положительной корреляции, для того, чтобы получить портфель с минимальным риском, необходимо коротко продать один из активов, и инвестировать все имевшиеся и вырученные за счет короткой продажи средства во второй актив. Поскольку коэффициент корреляции бумаг равен 1, то: где σ – уровень риска той или иной ценной бумаги. Отсюда: Доля А = 0,24/(0,24-0,19) = 4,8 Доля В = 0,19/(0,19-0,24) = - 3,8 То есть, доля рисковых бумаг В изначально должна составлять 380 %, но эти бумаги необходимо очень быстро продать, инвестировав средства в ценные бумаги А. Доходность такого портфеля будет равна: μр = 4,8*0,07+3,8*0,12 = 0,792 или 79,2 % Эта доходность будет обеспечена только в случае короткой продажи ценной бумаги Б и дальнейшего нахождения в портфеле только ценной бумаги А. 2. Определяем риск портфеля максимальной доходности. Поскольку ценная бумага В обладает максимальной из двух бумаг доходностью, то в случае, если портфель состоит только из бумаг В, он и будет характеризоваться максимальной доходностью. Риск такого портфеля будет равен: σр2 = ξB где ξB – риск ценной бумаги В Отсюда: σр = 0,24 = 4,8 или 480 % 12. Найти доходность к погашению облигации со сроком обращения 8 лет, номинальной стоимостью 3000 и купонной ставкой 8%, если: 1) она продаётся за 3000, 2) её розничная цена увеличится на 10%, 3) уменьшится на 5%. Решение 1) она продаётся за 3000, 300 = 240/R*[1-1/(1+R)^8] + 3000/(1+R)^8 R = 0,8 или 80 % 2) её розничная цена увеличится на 10%, 2) её розничная цена увеличится на 10% — 3000 *1,1 = 3300: 3300 = 240/R*[1-1/(1+R)^8] + 3000/(1+R)^8 R = 0.0636622 или 6.36 % 3) уменьшится на 5%? уменьшится на 5% — 3000 * 0,95 = 2850: 2850 = 240/R*[1-1/(1+R)^8] + 3000/(1+R)^8 R = 0,089000 или 89 % 13. Портфель состоит из двух ценных бумаг А и В, ожидаемые доходность и риск которых, выраженные в процентах, равны А(14; 27), В(37; 46). Коэффициент корреляции бумаг равен -1, а его доходность равна 20%. Найти портфель и его риск. Решение Решение. В случае полной корреляции портфелем минимального риска является безрисковый портфель. Его доходность по формуле 4.12 равна 14. Текущая цена актива равна 800 USD. Предполагается, что месяц спустя цена актива может быть равна 770 USD или 840 USD. В рамках однопериодной модели ценообразования опционов вычислить текущую стоимость месячного колл опциона на этот актив, цена исполнения которого равна 820 USD. Процентная ставка постоянна, выполняется непрерывно и равна 7% годовых. Решение S0 = 800 руб. S0u – цена актива в момент времени t = 1 в случае повышения = 840 руб.; S1(d) = S0d – цена актива в момент времени t = 1 в случае понижения = 760; Х0 – цена исполнения = 820 руб. Цена опциона в случае повышения = 840 - 820 = 20 руб. Стоимость опциона (1+0,07/12)*(820-800*(1+0,07/12) = 15,42 руб. Ответ 15,42 руб 15. Текущая цена актива равна 3000 руб. За год его стоимость может повысится на 18% или понизиться на 15%. Безрисковая годовая ставка равна 10%. Цена исполнения опциона «колл» со сроком исполнения в конце года равна 3150 руб. Определить величину премии за опцион. Решение Определим величину премии за опцион. Если цена актива вырастет и составит 1,18*3000 = 3540 руб., то владелец опциона воспользуется своим правом на покупку актива за 3000 рублей. Следовательно, цена опциона C1(u) составит 3540 –3150 = 390 руб. Если цена актива понизится и составит 0,85 * 3000 = 2550 руб., то владелец опциона свое право на покупку актива за 3150 рублей использовать не станет, и цена опциона C1(d) будет равна нулю. 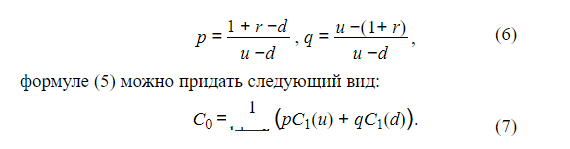 В соответствии с (6) и (7) находим коэффициенты:
и премию за опцион: C0 =1/1,1 *(0,7575*390 +0,2424* 0)= 268,6 руб. Ответ 268,6 руб | |||||||||||||||||||||||
