1-5(6 вариант). Решение. Используем Теорему 5 (сложение без повторения) Ответ 1,07 10 15 Задача 2 Условие
 Скачать 28.65 Kb. Скачать 28.65 Kb.
|
|
Задание 1. Условие На приёме у терапевта 18 человек, в день терапевт осматривает 15 человек. Сколькими способами можно составить очередь на приём к врачу? Дано: m=15 n=18 Решение. Используем Теорему 5 (сложение без повторения) 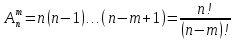 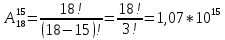 Ответ: 1,07 * 1015 Задача 2 Условие Какова вероятность того, что в написанном наудачу трёхзначном числе все цифры различны? Дано: Х Х Х n = 10 Решение. Решим задачу, используя Теорему умножения зависимых функций 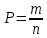 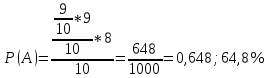 Ответ: 64,8% Задание 3 Условие Первый участок включает 25 человек, второй – 30 человек, третий – 20 человек, четвёртый участок – 15 человек. Вероятность полного выздоровления больных на первом участке – 0,78, на втором - 0,6, на третьем - 0,9, на четвёртом – 0,9. Найти вероятность полного выздоровления одного больного из этих участков. Дано: P(B) 1 25 2 30 3 20 4 15 Решение: А- полностью выздоровеет один больной. Bi – выбор участка, причем P(B1) = 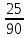 ; P(B2) = ; P(B2) = 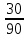 ; P(B3) = ; P(B3) = 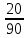 ; P(B4) = ; P(B4) = 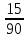 P(А/ B1) – вероятность того, что полностью выздоровеет один больной на первом участке = 0,78 P(A/B2) - вероятность того, что полностью выздоровеет один больной на втором участке = 0,6 P(A/B3) - вероятность того, что полностью выздоровеет один больной на третьем участке = 0,9 P(A/B4) - вероятность того, что полностью выздоровеет один больной на четвертом участке = 0,9. Пользуясь формулой полной вероятности, находим: P(A) = P(B1) * P(А/ B1) + P(B2) * P(A/B2) + P(B3) * P(A/B3) + P(B4) * P(A/B4) = 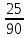 * 0,78 + * 0,78 + 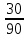 * 0,6 + * 0,6 + 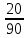 * 0,9+ * 0,9+ 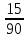 * 0,9 = 0,76 * 0,9 = 0,76Ответ: 76%. Задание 4. Найти вероятность доставания таблетки димедрола из коробки хотя бы один раз при четырёх попытках, если в коробке находятся 6 таблеток из них с димедролом 2. Дано: p= 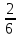 q=1-p = 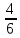 n=4 Решение: Вероятность извлечения хотя бы одной таблетки димедрола: P(A)= 1- 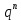 P(A)= 1- 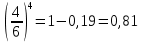 Ответ: 81% Задание 5. Для сдачи зачёта студентам необходимо подготовить 30 вопросов. Из 25 студентов 10 подготовили ответы на все вопросы, 8 – на 25 вопросов, 5 – на 20 вопросов и двое – на 15. Вызванный наудачу студент ответил на поставленный вопрос. Найти вероятность того, что этот студент подготовил только половину вопросов. Решение. Пусть А - событие «вызванный наудачу студент ответил на поставленный вопрос». В1 - «студент подготовил все вопросы», В2 - «студент подготовил 25 вопросов», В3 - «студент подготовил 20 вопросов», В4 - «студент подготовил 15 вопросов», Р(В1)А=1 - вероятность того, что студент, подготовивший все вопросы, ответит на поставленный вопрос; Р(В2)А= 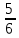 - вероятность того, что студент, подготовивший 25 вопросов, ответит на поставленный вопрос; аналогично, - вероятность того, что студент, подготовивший 25 вопросов, ответит на поставленный вопрос; аналогично,По формуле Байеса имеем 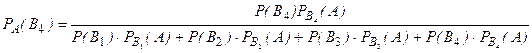 , т.е. , т.е.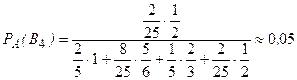 . .Ответ: |
