крепт. модель франка. Решение Используя формулу 1), решим уравнение с разделяющимися переменными
 Скачать 109.57 Kb. Скачать 109.57 Kb.
|
|
Цель: применение полученных навыков в системе Mathcad Задание 1. Аналитически решить в системе Mathcad нативную форму модели Франка с учетом подстановки. Удостовериться в правильности полученного решения. Ход решения внести в отчет. Сделать заключение и выводы. Решение: Используя формулу (2.1), решим уравнение с разделяющимися переменными. 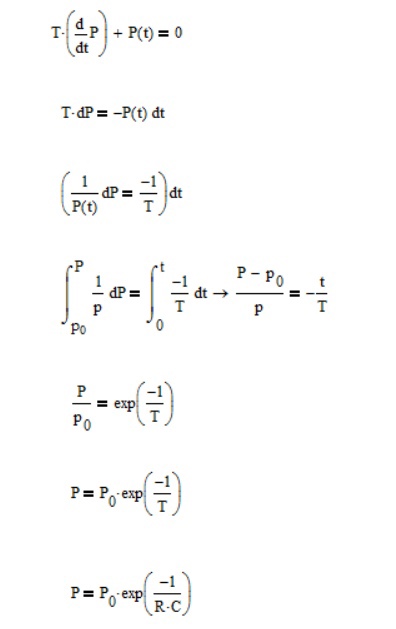 Из полученного выражения выражаем P, и используя подстановку T=R*C, получаем: 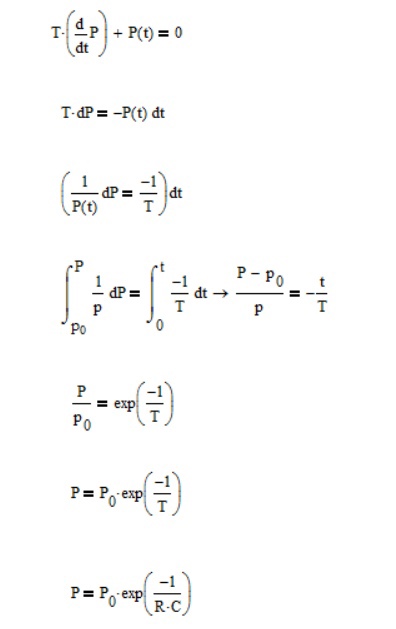 Рис.1 – получение формулы Франка с учетом подстановки Задание 2. Реализовать в среде Mathcad математическую модель Франка (2.3, 2.4) для P0 = 120 мм рт.ст. в диапазоне от 0 до 5 секунд. Подобрать такое значение модуля упругости сосудистой стенки С для постоянной времени Т при R = 100 мл/мм рт.ст, чтобы через 0,8. с давление в резервуаре снизилось с 120 мм.рт.ст. до 80 мм.рт.ст. Определить изменение минутного кровотока Q во времени. Результаты решения отобразить на графиках, синхронизовать вывод графиков P(t) и Q(t). Решение:  Рис.2 – подбор значения модуля упругости сосудистой стенки С для постоянной Т. |
