Решение Изобразим механизм в соответствии с данными

• Название: Решение Изобразим механизм в соответствии с данными
• Дата: 06.05.2023
• Размер: 153 Kb.
• Имя файла: RGR.doc
• Тип: Решение; #1112501

РГР 1

Задача К4а

Плоский механизм состоит из четырех стержней (1, 2, 3, 4) и ползуна 𝐵 соединенных друг с другом и с неподвижными точками 𝑂₁, 𝑂₂ шарнирами. Длины стержней ℓ₁=0.4м, ℓ₂=0.8м, ℓ₃=1.2м, ℓ₄= 0.6м. Точка 𝐾 всегда делит стержень пополам

Д ано:

=45

=135

=90

=75

=60

₄=3 c^–1

Найти:

V_E, V_K, V_B, ₁, ₂

Решение
1. Изобразим механизм в соответствии с данными варианта



2. Определим линейную скорость точки E при вращательном движении стержня 4:

V_E=₄l₄=30.6=1.8 м/с

Она направлена перпендикулярно стержню 4 в сторону вращения стержня (по ходу часовой стрелки).
3. Найдем линейную скорость точки 𝐴. Стержни являются абсолютно твердыми телами. Линейная скорость точки 𝐴 при вращательном движении стержня 1 должна быть направлена перпендикулярно стержню. Величину и направление скорости точки 𝐴 определим по теореме о проекциях скоростей двух точек плоской фигуры (стержня 𝐴𝐸), зная скорость точки Е

V_Ecos0=V_Acos45

V_A=V_Ecos0/cos45=1.81/0.707=2.55 м/с
Угловая скорость первого стержня.

Звено 1 вращается по ходу часовой стрелки с угловой скоростью



Угловая скорость второго стержня и линейная скорость точки 𝐾.

Для определения величины и направления скорости точки 𝐾 необходимо найти М.Ц.С. второго звена. По определению он находится на пересечении перпендикуляров к векторам скоростей точек 𝐴 и 𝐸, то есть в точке 𝑃₂. Следовательно, стержень 2 будет совершать мгновенно вращательное движение относительно М.Ц.С. против хода часовой стрелки с угловой скоростью 𝜔₂.

ЕP₂=AE=l₂=0.8 м

KP₂=



Вычислим скорость точки 𝐾:

V_K=₂KP₂=2.250.89=2.0 м/с

Вектор скорости этой точки перпендикулярен к расстоянию до М.Ц.С. 𝐾𝑃₂ и направлен в сторону вращения звена 2.
Скорость точки В и угловая скорость стержня 3. Движение звена 3 − плоское, для нахождения его угловой скорости 𝜔₃ найдем М.Ц.С. стержня 3. Направление скорости точки 𝐵 определяется направляющими ползуна, которому принадлежит эта точка.

По теореме о проекциях скоростей найдем

V_Kcos78=V_Bcos30

V_B= V_Kcos78/cos30=2.00.208/0.866=0.48 м/с
Ответ: V_E=1.8 м/с; V_K=2.0 м/c; V_B=0.48 м/с; ₁=6.36 с^–1; ₂=2.25 с^–1.
РГР2

Задача С3

Определить реакции опор жесткой рамы.

Д ано:

М=25 кНм

q=6 кН/м

F=35 кН

1. Выберем объект равновесия.

В качестве такового здесь удобно рассмотреть раму ADTB.
2. Приложим заданные нагрузки.

Силу F; пару с моментом М; равномерно распределенную нагрузку на участке KC заменим равнодействующей Q , приложенной в середине участка KC

Q=qKC=66=36 кН

3. Заменим действие связей реакциями:

Неподвижный шарнир в точке K заменим двумя реакциями Х_K, Y_K. Подвижный шарнир в точке В заменим одной реакцией R_B .

Реакцию R_B разложим на две составляющие:

R_Bx=R_Bsin60=0.866R_B

R_By=R_Bcos60=0.5R_B

Завершим формирование расчётной схемы выбором осей координат Kху.



4. Составим уравнения равновесия. Приложенная к объекту равновесия система сил является произвольной плоской.

F_kx= –F+X_K–R_Bx=0 (1)

M_K(F_k)= –M–F4–Q3+R_By4–R_Bx5=0 (2)

M_B(F_k)=Q1–M+F1–X_K5–Y_K4=0 (3)
5. Определение искомых величин.

Из уравнения равновесия (2) получим:

–M–F4–Q3+0.5R_B4–0.866R_B5=0

R_B=(–M–F4–Q3)/(–0.54+0.8665)=(–25–354–363)/(–0.54+0.8665)= –117.17 кН

Из уравнения (1) имеем:

X_K=F+R_Bx=35–117.170.866= –66.47 кН

Из уравнения (3) имеем:

Y_K=(Q1–M+F1–X_K5)/4=(361–25+351+66.475)/4=94.58 кН
6. Проверка.

Для проверки полученных результатов составим такое новое уравнение равновесия, чтобы в него входили все найденные величины. Это, например, может быть уравнение моментов относительно точки А. При подстановке в такое уравнение найденных реакций оно должно обратиться в тождество.

M_A(F_k)=0

–M+Y_K2–X_K4–Q5+R_By6–R_Bx1=

= –25+94.582+66.474–365+0.5(–117.17)6–0.866(–117.17)1= –556.51+556.51=0
Ответ: X_K= –66.47 кН; Y_K=94.58 кН; R_B= –117.17 кН.

РГР3

Задача С5

Определить реакции внешних связей составной рамы.

Д ано:

М=30 кНм

q=6 кН/м

F=30 кН
1. Изображение конструкции в положении, соответствующем конкретным значениям данных о ее геометрических характеристиках.
2. Выбор тела (тел), равновесие которого должно быть рассмотрено (объект равновесия). В задаче помимо реакции внешних опор необходимо определить давление в промежуточном шарнире С, поэтому для решении задачи применим метод разбиения.

Расчленим мысленно конструкцию по шарниру С на две части и рассмотрим равновесие каждой части отдельно.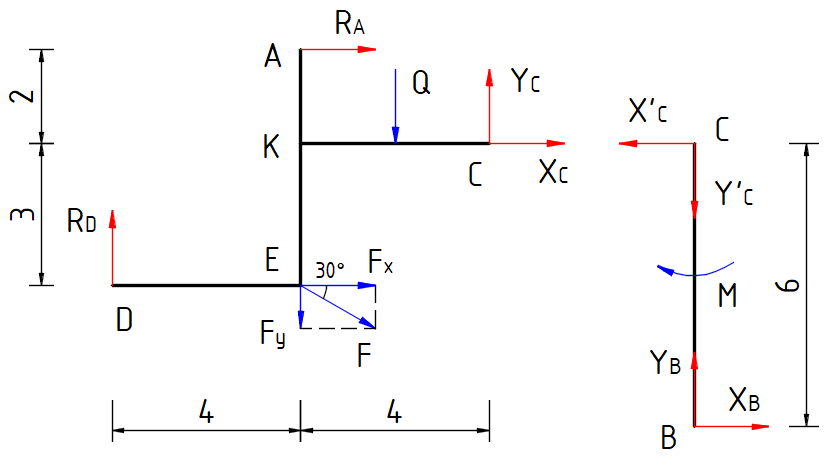



3. Изображение сил, действующих на выбранные объекты равновесия.
Сосредоточенную силу F разложим на составляющие:

F_x=Fcos30=300.866=25.98 кН

F_y=Fsin30=300.5=15 кН
Действие равномерно распределенной нагрузки интенсивности q=6кН/м заменим сосредоточенной силой Q=q4=64=24 (кН), которая будет приложена к середине участка распределения KC.
При расчленении конструкции внутренний шарнир С для каждой из частей конструкции DKC и BС является неподвижным цилиндрическим шарниром, действие которого заменяется двумя реакциями Х_C и Y_С (приложены к части конструкции DKС). При этом:

X_C=X’_C, Y_C=Y’_C .

4. Составление уравнений равновесия

Уравнения равновесия (а) – (с) для части конструкции DKС будут иметь вид:

F_kx=R_A+F_x+X_C=0 (a)

F_y=R_D–F_y–Q+Y_C=0 (b)

M_C(F_k)=Q2–R_A2+F_x3+F_y4–R_D8=0 (c)

Уравнения равновесия (d) – (f) для части конструкции BС запишутся в виде:

F_kx= –X’_C+X_B=0 (d)

F_ky= –Y’_C+Y_B=0 (e)

M_C(F_k)= –M+X_B6=0 (f)
5. Определение искомых величин и исследование полученных результатов.

В шести уравнениях (a) – (f) шесть неизвестных величин, то есть, число неизвестных величин совпадает с числом уравнений равновесия. Следовательно, все неизвестные величины могут быть найдены из уравнений равновесия.

Из (f):

X_B=M/6=30/6=5 кН

Из (d):

X’_C=X_B=5 кН

Из (а):

R_A= –F_x–X_C= –25.98–5= –30.98 кН

Из (с):

R_D=(Q2–R_A2+F_x3+F_y4)/8=(242+30.982+25.983+154)/8=30.99 кН

Из (b):

Y_C= –R_D+F_y+Q= –30.99+15+24=8.01 кН

Из (а):

X_C= –R_A–F_x=30.98–25.98=5 кН

Из (e):

Y_B=Y’_C=8.01 кН
6. Проверка полученных результатов. Для проверки составим уравнение моментов для «замороженной» конструкции. Так как в проверочное уравнение должны входить все или большее число искомых реакций, то выберем в качестве моментной точку E.

M_E(F_k)= –R_D4–R_A5–Q2–M+Y_B4+X_B3=

= –30.994+30.985–242–30+8.014+53= –201.96+201.94= –0.02

Незначительная погрешность свидетельствует о верности решения.
Ответ: R_A= –30.98 кН; X_B=5 кН; Y_B=8.01 кН; X_C=5 кН; Y_C=8.01 кН; R_D=30.99 кН.