Главная страница
Навигация по странице:

  • ИДЗ 16.1. 2 .

  • Решение

  • ИДЗ 16.2.2.

    		•

    Операционное исчисление. ИДЗ_операционное исчисление_1вар.. Решение Коэффициенты даны Подставляя их в выражение для функции получаем


    Скачать 278 Kb.
    НазваниеРешение Коэффициенты даны Подставляя их в выражение для функции получаем
    АнкорОперационное исчисление
    Дата22.12.2021
    Размер278 Kb.
    Формат файлаdoc
    Имя файлаИДЗ_операционное исчисление_1вар..doc
    ТипРешение
    #314401

    ИДЗ 16.1.1. По заданному оригиналу найти изображение по Лапласу: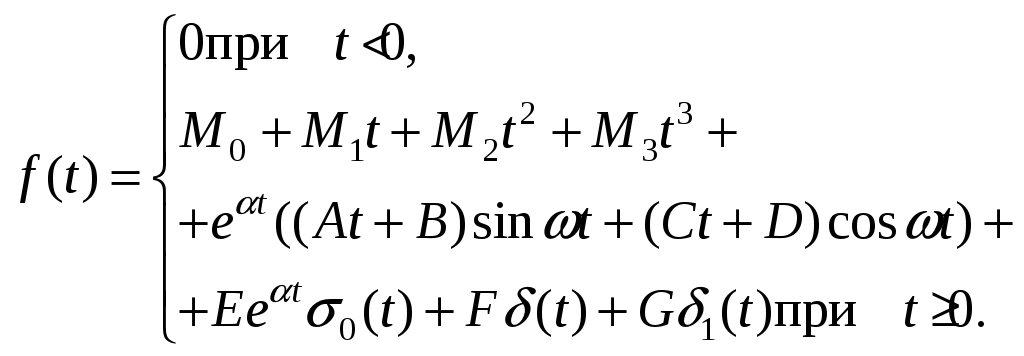



    Значения параметров приведены в таблице.

    № варианта


























    1.1
    0
    1
    0
    2
    0
    0
    2
    1
    0
    0
    3
    0
    0


    Решение: Коэффициенты даны:

    .

    Подставляя их в выражение для функции получаем:



    Для отыскания изображения находим оригиналы всех функций-слагаемых:



    На основании свойства линейности получаем:



    ИДЗ 16.1.2. Найти изображение функции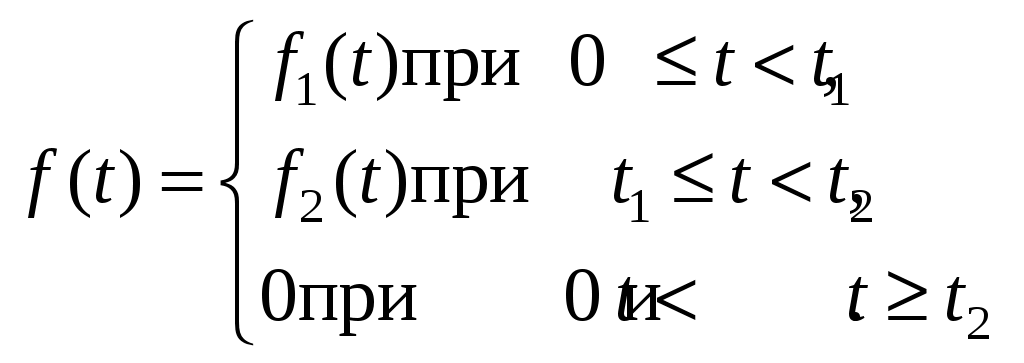



    Функции и числовые значения параметров приведены в таблице.

    № варианта








    2.1




    1
    2


    Решение: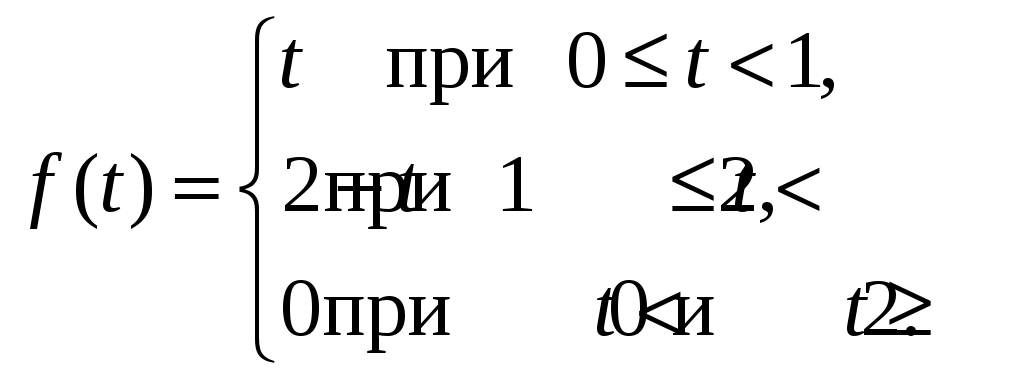



    С помощью единичной функции Хевисайда представим функцию 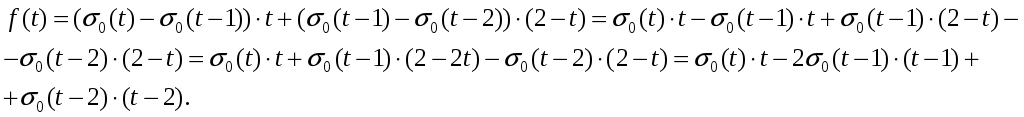в следующем виде:



    Так как и , то на основании теоремы запаздывания имеем:



    Следовательно,



    ИДЗ 16.1.3. По заданному изображению



    найти оригинал. Значения коэффициентов приведены в таблице.

    № варианта












    3.1
    3
    -9
    16
    -2
    -6
    13


    Решение: Подставим в изображение заданные коэффициенты:



    Разложим знаменатель дроби на линейные множители и представим данную дробь в виде суммы простейших рациональных дробей:



    Приведя сумму дробей в правой части равенства к общему знаменателю, приравняем числители дробей:



    Приравняв коэффициенты при одинаковых степенях, получим систему уравнений для определения коэффициентов A, B, C: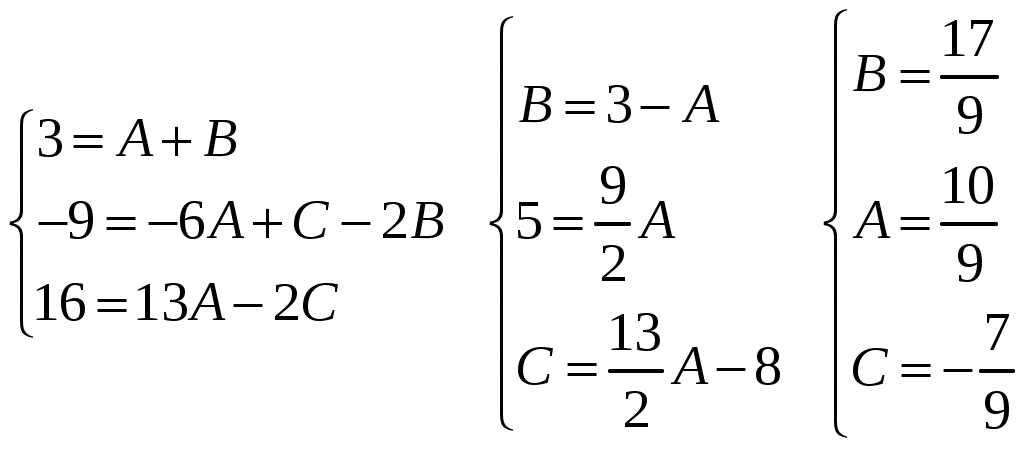



    Следовательно,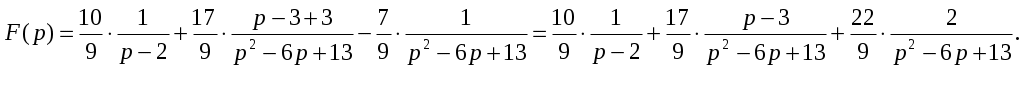



    Перейдем от изображений к соответствующим оригиналам: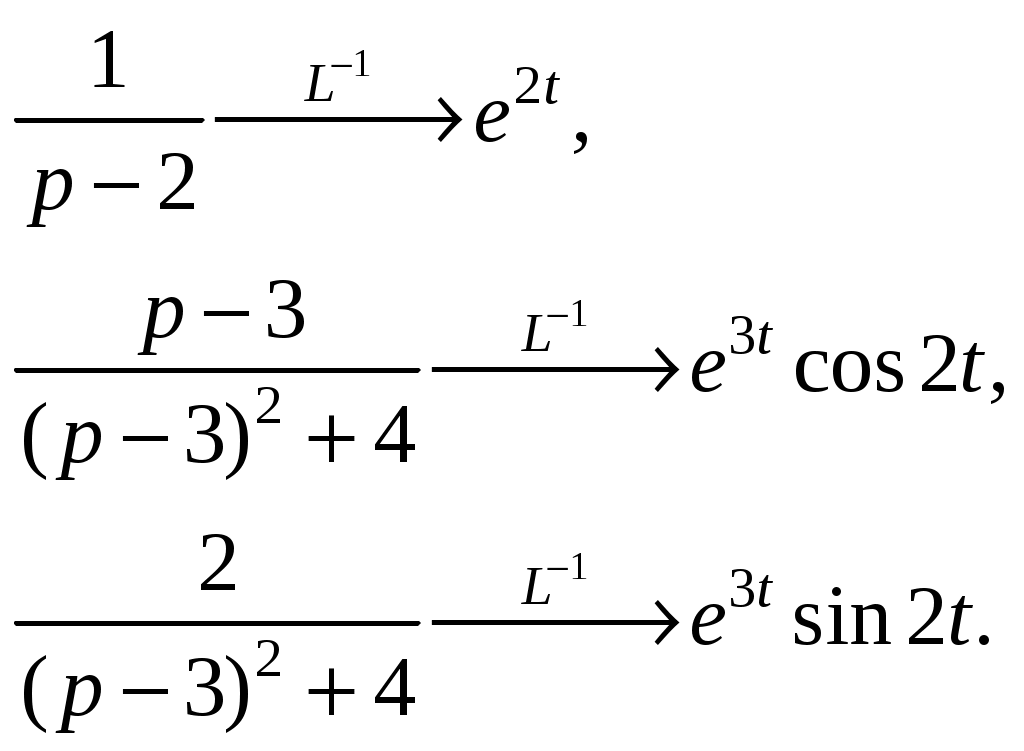





    ИДЗ 16.2.1. Решить операторным методом линейное дифференциальное уравнение



    Функцию и значения коэффициентов приведены в таблице.


    № варианта














    1.1
    0
    1
    1


    0
    0,5
    -1


    Решение:



    Перейдем от оригиналов к изображениям: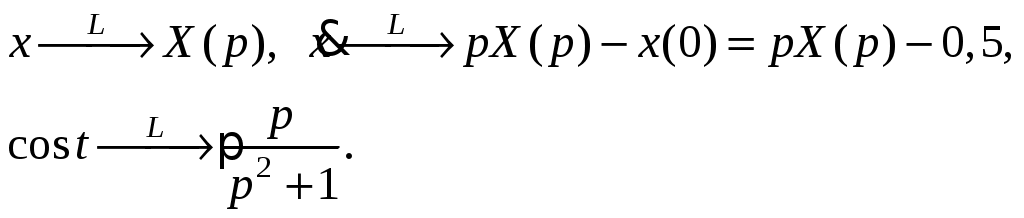



    Получим операторное уравнение:

    Решаем его относительно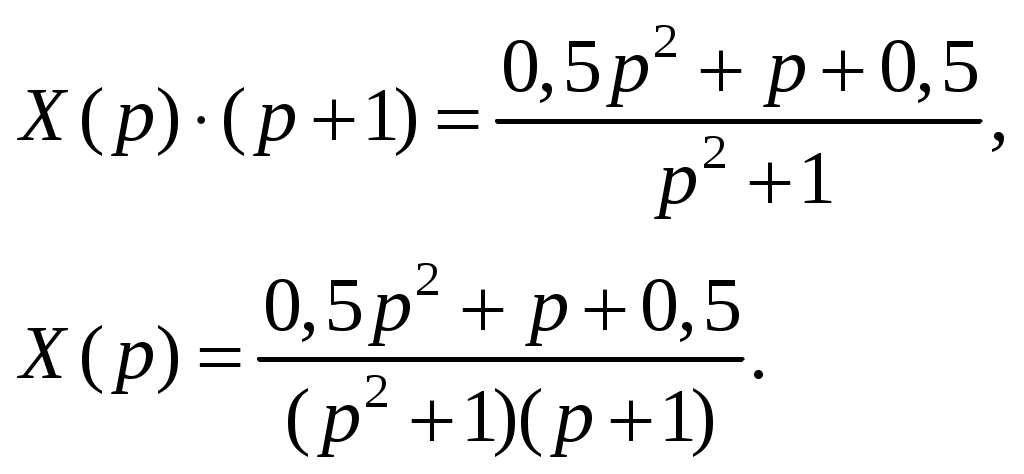



    Представим данную дробь в виде суммы простейших рациональных дробей:



    Приведя сумму дробей в правой части равенства к общему знаменателю, приравняем числители дробей:



    Приравняв коэффициенты при одинаковых степенях, получим систему уравнений для определения коэффициентов A, B, C: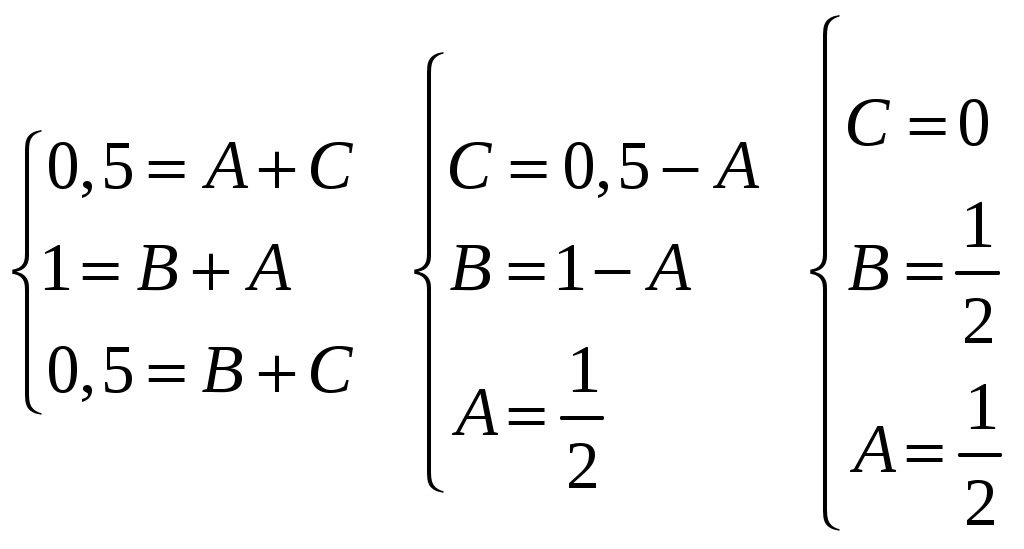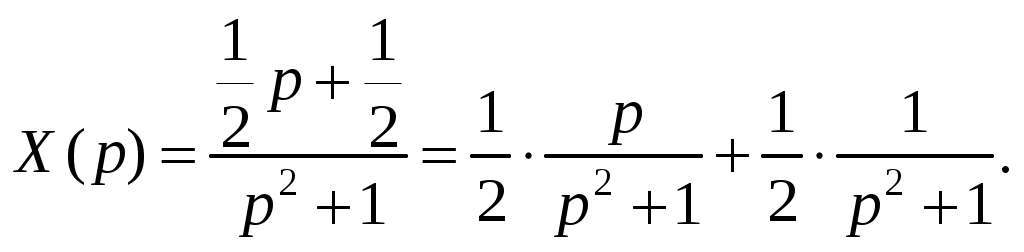





    Перейдем от изображений к соответствующим оригиналам: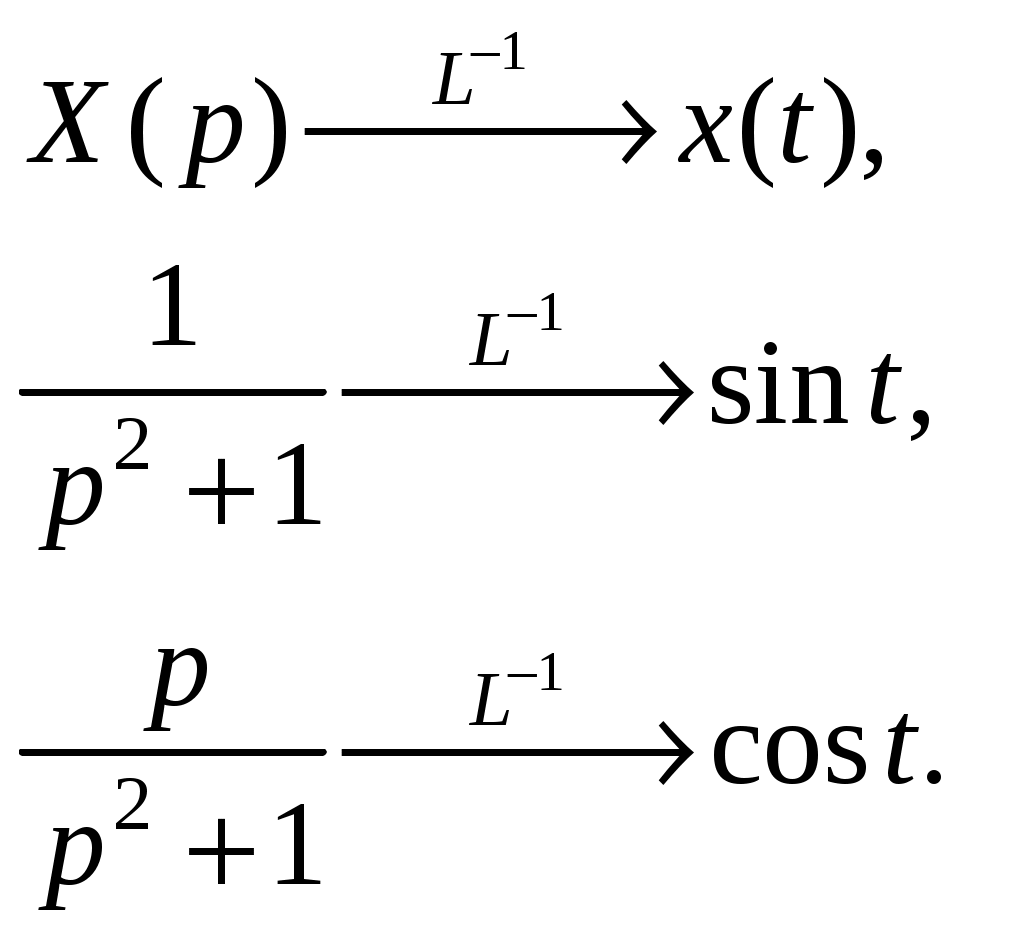



    Получим искомое решение дифференциального уравнения:



    ИДЗ 16.2.2. Решить операторным методом систему линейных дифференциальных уравнений



    Функции и значения приведены в таблице.

    № варианта
























    2.1
    1
    0
    0
    1
    0
    0
    1
    -2
    -2
    0
    1
    1


    Решение: Подставим в систему заданные коэффициенты:

    .

    Перейдем от оригиналов к изображения:



    Получаем систему операторных уравнений:



    Решив ее относительно X и Y, будем иметь:





    Перейдем от изображений к соответствующим оригиналам: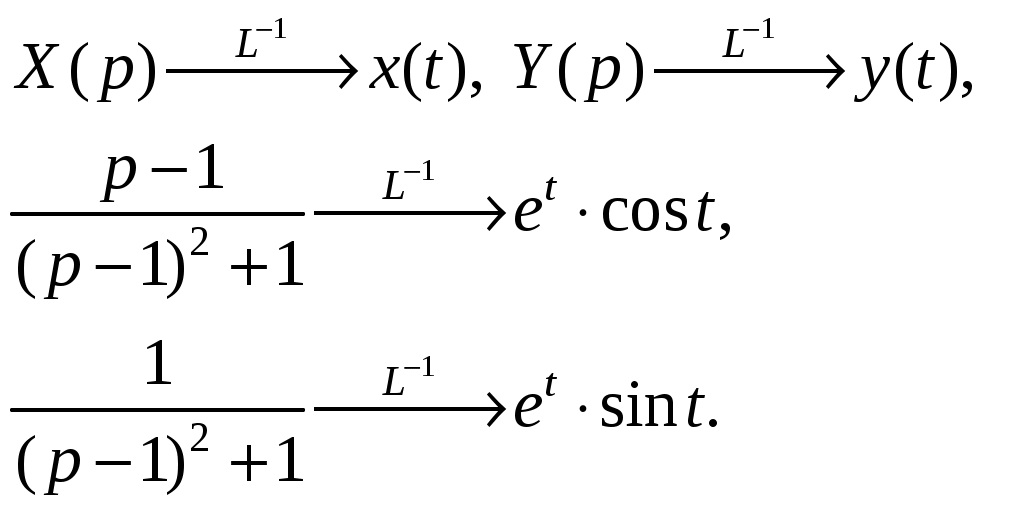



    Получим искомое решение системы уравнений: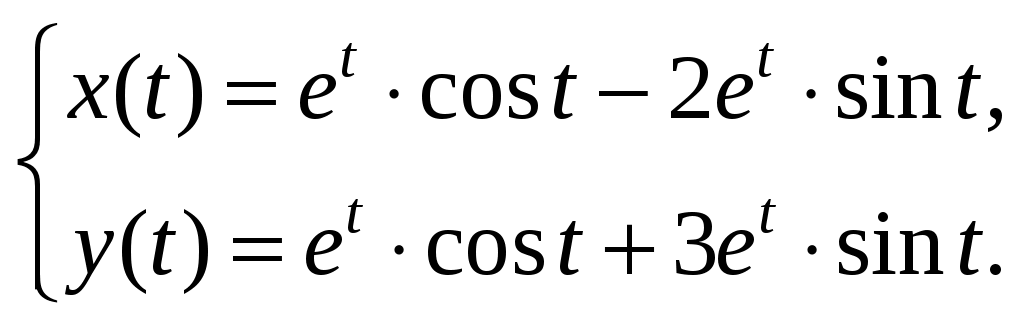

    написать администратору сайта