ОТИ. ОТИ!. Решение Количество информации, содержащейся в каждом из символов источника при их независимом выборе
 Скачать 46.07 Kb.
|
|
Тема 2 1. Вычислить количество информации выдаваемой источником, если размерность алфавита X={x1, x2, …, xm} равна m=3. Вероятности появления символов источника равны: p1=0,15; p2=0,5; p3=0,35. Решение: Количество информации, содержащейся в каждом из символов источника при их независимом выборе: 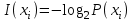 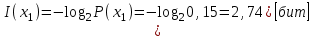 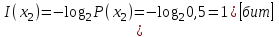 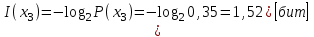 Количества информации: 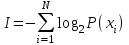 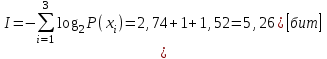 Тема 3 5. Является ли код 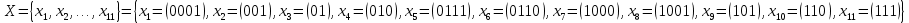 однозначно декодируемым?Решение: Для построения однозначно декодируемого q-ичного кода, содержащего m кодовых слов с длинами n1, n2, …, nm необходимо и достаточно, чтобы выполнялось неравенство Крафта 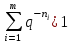 где q обозначает число символов кодового алфавита. n1=n5=n6=n7=n8=4 n2=n4=n9=n10=n11=3 n3=2 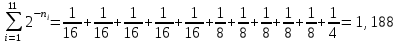 Неравенство Крафта не выполняется, значит данный код не является однозначно декодируемым. Тема 4 2. Источник формирует символы X={x1; x2} с вероятностями 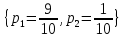 .. Имеется блоковый источник с трехкратным расширением X3={c1, c2, c3, c4, c5, c6, c7, c8,}. Для кодирования блокового источника применяется следующий префиксный код:c1→(1); c2→(011); c3→(010); c4→(001); c5→(00011); c6→(00010); c7→(00001); c8→(00000); Вычислить: 2.1. Энтропию источника. 2.2. Энтропию блокового источника. 5.3. Среднюю длину слова декодируемого кода. 5.4. Среднюю длину слова на один символ источника X. Решение: Энтропия источника одиночных символов равна 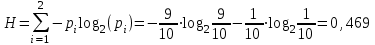 бит/символВычисляем вероятности появления символов источника X3. 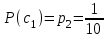 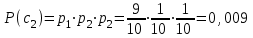 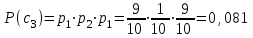 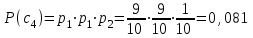 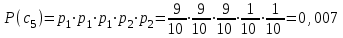 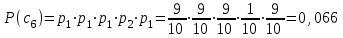 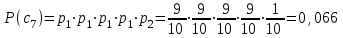 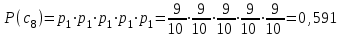 Энтропия блокового источника равна: 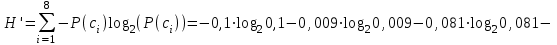 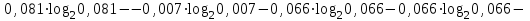 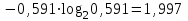 бит/символСредняя длина слова декодируемого кода.: 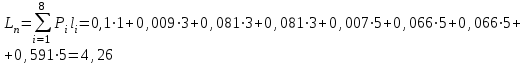 Средняя длина слова на один символ источника X: 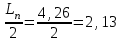 Тема 10 4. Определить ошибку декодирования кода [6, 3, 3] в канале с вероятно-стью ошибки на символ 𝑝=0,01, используя стандартное расположение для кода, представленного матрицей 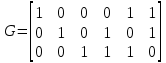 |