Решение Количество информации, содержащейся в каждом из символов источника при их независимом выборе
 Скачать 130.41 Kb. Скачать 130.41 Kb.
|
|
Контрольное задание № 1 1. Вычислить количество информации выдаваемой источником, если размерность алфавита X={x1, x2, …, x6} равна m=6. Вероятность появления события p1=0,05; p2=0,15; p3=0,05; p4=0,4; p5=0,2; p6=0,15. Решение: Количество информации, содержащейся в каждом из символов источника при их независимом выборе: 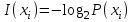 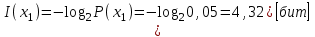 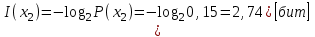 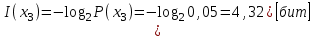 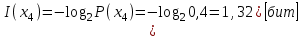 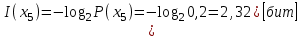 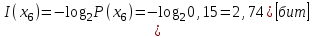 Значение количества информации: 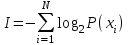 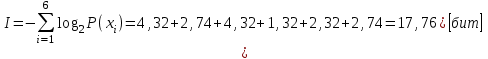 2. Источник формирует следующие символы 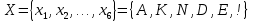 . .Вероятности символов задаются множеством: 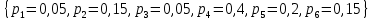 . .Вычислить энтропию дискретного источника. Решение: Энтропия источника информации – это средняя информация, полученная для всех возможных событий. Энтропия дискретного источника без памяти с символами алфавита X={x1, x2, …, xm} и соответствующими вероятностями p1, p2, …, pm равна 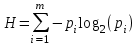 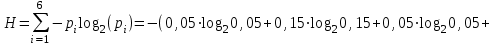 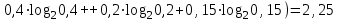 бит/символ бит/символ3. Используются следующие кодовые слова длиной 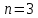 равномерного кода равномерного кода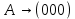 ; ;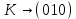 ; ;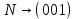 ; ;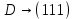 . .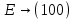 . .Удовлетворяет ли код неравенству Крафта? Решение: Для построения однозначно декодируемого q-ичного кода, содержащего m кодовых слов с длинами n1, n2, …, nm необходимо и достаточно, чтобы выполнялось неравенство Крафта 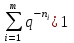 где q обозначает число символов кодового алфавита. n1=n2=n3=n4=n5=n=3 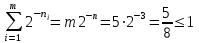 Неравенство Крафта выполняется, значит данный код однозначно декодируемый. 4. Пусть используется префиксный код со словами: 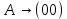 ; ;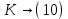 ; ; 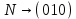 ; ;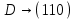 ; ;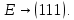 Вероятности символов источника характеризуются множеством 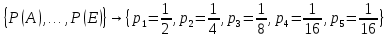 . .Вычислить среднюю длину кодового слова. Решение: Мерой эффективности кода является его средняя длина кодовых слов 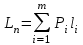 где m – число символов источника с n-кратным расширением источника одиночных символов, P1, P2, …, Pm – вероятности символов источника с n-кратным расширением, l1, l2, …, lm – длина соответствующих кодовых слов. Для построения этого кода использовались символы двоичного источника X={0,1}. Код имеет среднюю длину: 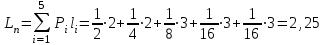 5. Источник формирует символы X={x1; x2} с вероятностями 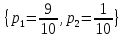 .. Имеется блоковый источник с трехкратным расширением X3={c1, c2, c3, c4, c5, c6, c7, c8,}. Для кодирования блокового источника применяется префиксный код: .. Имеется блоковый источник с трехкратным расширением X3={c1, c2, c3, c4, c5, c6, c7, c8,}. Для кодирования блокового источника применяется префиксный код:c1→(1); c2→(011); c3→(010); c4→(001); c5→(00011); c6→(00010); c7→(00001); c8→(00000); 5.1. Вычислить энтропию источника. 5.2. Вычислить энтропию блокового источника. 5.3. Вычислить среднюю длину слова декодируемого кода. 5.4. Вычислить среднюю длину слова на один символ источника X. Решение: Энтропия источника одиночных символов равна 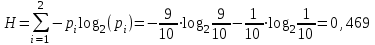 бит/символ бит/символВычисляем вероятности появления символов источника X3. 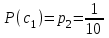 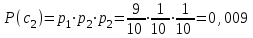 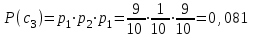 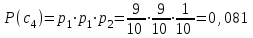 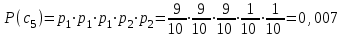 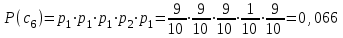 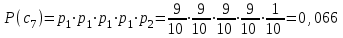 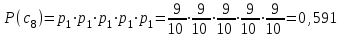 Энтропия блокового источника равна: 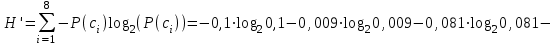 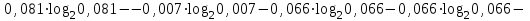 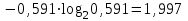 бит/символ бит/символСредняя длина слова декодируемого кода.: 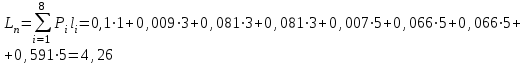 Средняя длина слова на один символ источника X: 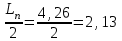 6. Показать, что группа 𝐺 = < {0,1, 2, 3, 4, 5}; +; 0> содержит подгруппы порядков: 1, 2, 3 и 6. Решение: Если g — элемент группы G такой, что gn = 1 для некоторого n, и р — наименьшее положительное целое число такое, что gp = 1, тогда множество {g, g2,..., gp} является подгруппой группы G. g1=g g2= g2 g3= g3 g6=1 Cледовательно, множество {g, g2,..., g6} является подгруппой группы G. 7. Найти расстояния Хэммингавекторов: 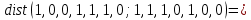 , ,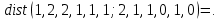 Решение: Расстоянием Хемминга между двумя кодовыми словами называется количество отличных бит на соответствующих позициях 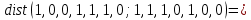 4 4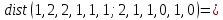 5 58. Построить порождающую 𝐺 и проверочную 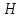 матрицу линейного группового кода с проверкой на четность с параметрами [𝑛; 𝑛 ‒1; 2], 𝑘 =3. матрицу линейного группового кода с проверкой на четность с параметрами [𝑛; 𝑛 ‒1; 2], 𝑘 =3.Решение: Порождающая матрица: 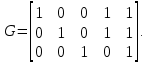 Проверочная матрица: 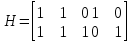 . .k = 3 – кол-во информационных символов, r = 2 – кол-во проверочных символов в кодовом слове, n = 5 – длина кодового слова. 9. Показать построение и реализацию принципиальной схемы кодера, используя проверочную Н матрицу. Основными функциями кодера являются: 1) преобразование входной информации Q(х) из последовательного кода в параллельный код; 2) формирование проверочных символов; 3) формирование кодовой последовательности F(х) путем последовательного объединения “k” информационных символов и l = n-k проверочных символов в единый кодовый поток. Для реализации данных функций в кодере необходимы следующие функциональные блоки: КРИ – 1/ k (КРИ – 1/3) – коммутатор распределения входной информации на “ k ” (k = 3) подпотоков; ФПСк – формирователь проверочных символов кодера; КОИ – n/1 (КОИ – 5/1) –коммутатор объединения информации “n” (n =5) параллельных подпотоков в единый поток; ФСУк – формирователь сигналов управления КРИ – 1/3 и КОИ – 5/1 кодера. В соответствии с этим обобщенная структурная схема кодера будет иметь следующее построение (рис.1) 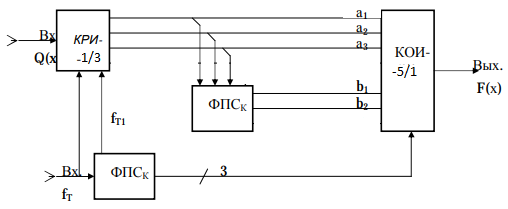 Рисунок 1 – Обобщенная структурная схема кодера В кодере, в соответствии с проверочной матрицей, ФПСк формирует проверочные символы b1b2, которые поступают на соответствующие входы КОИ – 5/1 и далее передается вслед за информационными символами в канал связи, образуя тем самым кодовую последовательность F(x). 10. Используйте метод синдромного декодирования линейного группового кода (п.8) для контроля над ошибками, если получены слова у1=0101, у2=1011. Решение: 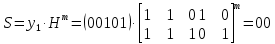 ⇒ кодовое слово принято без ошибок. ⇒ кодовое слово принято без ошибок.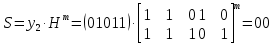 ⇒ кодовое слово принято без ошибок. ⇒ кодовое слово принято без ошибок.11. Показать построение и реализацию принципиальной схемы синдромного декодера, используя проверочную Н матрицу (п.8). Решение: Основными функциями декодера являются: 1) преобразование кодовой последовательности F'(х) из последовательного кода в параллельный код; 2) формирование проверочных символов (b1',b2',b3') из принятых информационных символов a1'… a4' в соответствии с проверочной матрицей; 3) формирование символов синдромной последовательности (синдрома) S1… S4; 4) дешифрация (анализ) синдрома и принятие решения о достоверности принятых информационных символов; 5) преобразование информационных символов из параллельного кода в последовательный код и выдача информационного блока символов θ (х) получателю. Для реализации данных функций в декодере необходимы следующие функциональные блоки: КРИ – 1/n (КРИ - 1/5) – коммутатор распределения информации на n (n=5) параллельных подпотоков; КОИ - k /1 (КОИ – 3/1) – коммутатор объединения информации к (к=3) параллельных подпотоков в последовательный поток; ФПСд – формирователь проверочных символов декодера; ФСС – формирователь синдромных символов; АС – анализатор (дешифратор) синдрома; ФСУд – формирователь сигналов управления (КРИ - 1/5) и (КОИ – 3/1) декодера. В соответствии с этим обобщенная структурная схема декодера, реализующего синдромный алгоритм декодирования, будет иметь следующее построение (рис.2). 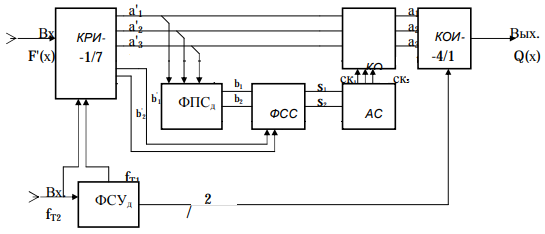 Рисунок 1 – Обобщенная структурная схема декодера Декодер работает следующим образом. Входные символы принятой кодовой последовательности F′(x) в КРИ –1/5 распределяется на пять параллельных подпотоков. Информационные символы a1'… a3' одновременно поступают на соответствующие входы КО и ФПСд. ФПСд формирует проверочные символы b1… b2 из принятых информационных символов в соответствии с проверочной матрицей. Сформированные проверочные символы поступают на соответствующие входы ФСС, на другие входы которого поступают принятые проверочные символы b1'… b2'. Синдромные символы S1,S2, формируются по правилу: S1 = b1Åb1'; S2 = b2Åb2'. Следовательно, синдромный вектор или синдром Sί(x) в данном случае будет содержать два двоичных символа, т.е. S(x)= S1, S2. 12.а. Источник имеет следующие символы алфавита с их вероятностями появления:
Постройте кодовое дерево Хаффмана. 12.б. Запишите код Хаффмана. Решение: а) Алгоритм Хаффмана изящно реализует общую идею статистического кодирования с использованием префиксных множеств и работает следующим образом: 1. Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте. 2. Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагаем равной сумме вероятностей составляющих его символов. В конце концов построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него. 3. Прослеживаем путь к каждому листу дерева, помечая направление к каждому узлу (например, направо - 1, налево - 0) . Полученная последовательность дает кодовое слово, соответствующее каждому символу. Построим кодовое дерево для сообщения со следующим алфавитом:
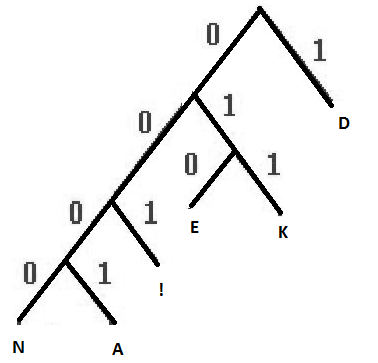 б) Запишем код Хаффмана.
|
