открытый урок. Решение линейных неравенств
 Скачать 89.45 Kb. Скачать 89.45 Kb.
|
|
Тема: Решение линейных неравенств. Тип урока: Урок закрепления знаний Цель урока: овладение математическими знаниями и умениями при решении линейных неравенств Задачи: Образовательные -вспомнить, что такое линейное неравенство; -повторить, что значит решить неравенство; -закрепить алгоритм решения линейных неравенств Воспитательные -развитие познавательного интереса; -развитие умения самостоятельно добывать знания и делать выводы; -развитие математической речи учащихся; -формирование элементов алгоритмической культуры; -развивать умение решать линейные неравенства. Развивающие -воспитывать у учащихся познавательную активность, самостоятельность, интерес к предмету Планируемы результаты: Личностные: Умение общаться в коллективе, слушать собеседника и вести диалог, аргументировать свою точку зрения. Развивать активность и находчивость при решении задач. Метапредметные: Увидеть роль и место математики в других дисциплинах и окружающей жизни; уметь обрабатывать информацию; выбирать способы решения неравенств в зависимости от конкретных условий; контролировать и оценивать процесс и результаты своей деятельности Предметные: уметь решать линейные неравенства; графически изображать множество их решений, а также записывать решения в виде числового промежутка; производить отбор решений по заданному условию (целые решения, наибольшее/наименьшее целое решение). Формы работы обучающихся: фронтальная, индивидуальная, работа в парах. Методы: по источникам знаний: словесный, наглядный; по степени взаимодействия учитель-ученик: эвристическая беседа; относительно дидактических задач: применение умений и навыков; относительно характера познавательной деятельности: репродуктивный, частично-поисковый. Оборудование: Компьютер, проектор, презентация. Учебник: Мерзляк А.Г, Полонский В.Б, Якир М.С. Алгебра. 9 класс. Москва Издательский центр «Вентана - Граф», 2017 Структура урока. Организационный этап. Цель: Проверить готовность к уроку. Инструктаж по работе с листом самооценки. Мотивация к учебной деятельности. Цель: Организовывать познавательную деятельность учащихся. Сформулировать тему и цели урока. Проверка домашнего задания. Цель: Проверка выполнения домашнего задания, воспроизведение и коррекция знаний. Актуализация знаний. Цель: Актуализация опорных знаний и способов действий Первичное закрепление ранее изученного материала. Цель: Организовать осмысленное применение полученных знаний Физкультминутка. Цель: Снятие зрительного напряжения. Повторение. Цель: Обеспечить осмысленное усвоение и закрепление знаний, организовать в работу в парах. Самооценка деятельности. Домашнее задание. Цель: Формирование личной ответственности за результаты деятельности. Итоги урока. Рефлексия. Цель: соотнесение цели урока и его результатов, самооценка работы на уроке. Ход урока: 1. Организационный момент: Здравствуйте, ребята, присаживайтесь. Прозвенел уже звонок, начинается урок. Мы сегодня не одни - гости на урок пришли. Мы должны им показать, что умеем хорошо работать, то есть - решать задачи. -Какое у каждого сегодня настроение, поднимите соответственно число пальцев. 2. Мотивация к учебной деятельности. Эпиграф к уроку (Слайд 1). Мы в прошлом уроке начали рассматривать с вами очень важную и сложную тему «Решение линейных неравенств» (Слайд 2). Правило 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не изменив при этом знак неравенства (Слайд 3). Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства (Слайд 4). Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный (Слайд 5). Чтобы каждый из вас получил сегодня оценку, вам необходимо будет поработать с листом самооценки знаний. Что это такое - вы знаете, прошу вовремя его заполнять. Психологическая установка учащимся: 1. Сегодня мы продолжим решать простые неравенства с одной переменной 2.На уроке разрешается: ошибаться, сомневаться, консультироваться, рассуждать и доказывать (Слайд 6). 3.Дать самому себе установку: «понять и быть тем первым, который увидит ход решения». 3. Проверка домашнего задания. Карточки (Слайд 7); Карточки (Слайд 8). 4. Актуализация знаний Цель: Актуализация опорных знаний и способов действий - Итак, открыли тетради, записали число. Классная работа. - Нашу работу я хочу начать словами Н.К. Крупской: «Математика- это цепь понятий; выпадет одно звенышко - и непонятно будет дальнейшее» (Слайд 9). Проверим, насколько крепка цепь наших знаний. Сначала зарядка для ума - устный счет (Слайд 10). 1)Укажите все целые числа, принадлежащие промежутку: [-6; 6]; 2)Укажите какое – либо число, принадлежащее промежутку (4,5; 4,6 ); 3)Принадлежит ли промежутку [9; 51] число 40,9 4)Существует ли в промежутке [8;41]; наибольшее число; наименьшее число? 5. Первичное закрепление ранее изученного материала. Цель: организовать осмысленное применение полученных знаний. Работа по карточкам Решить неравенства. Показать решение на числовом луче и записать в виде промежутка. 1) 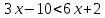 (Слайд 11) 2) (Слайд 11) 2)  (Слайд 12) (Слайд 12)Проблема: 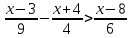 (слайд 13) (слайд 13)6. Физминутка для глаз: (Слайд 14,15) 7. Повторение. Тест. Цель: обеспечить осмысленное усвоение и закрепление знаний, организовать работу в парах. Работа у доски № 132, остальные в тетради. 1 вариант Самостоятельная работа (Верно-1, неверно - 0) Является ли число -5 решением неравенства 2х ≥ 10 Является ли число 6 решением неравенства 2х ≥ 10 Является неравенство 2х+8 ≥ 3 строгим Соответствует ли неравенство -2 ≤ х ≤ 5 промежутку (-2;5) Соответствует ли промежуток (5, +∞) неравенству х ≤ 5 Соответствует ли промежуток (1;7) изображению  7. Соответствует ли изображение промежутку Х ≤ 10  8. Число 8 является наибольшим целым числом неравенства х ≥ 8 Один вопрос считается 1балл. Всего 8балл. «5» - 7-8 балл, «4» - 5-6 балл, «3» - 4 балл, «2» - меньше 3балла. Код ответа: 01000010 (Слайд 16) 2 вариант 1. Является ли число -3 решением неравенства 3х ≥ 9 2. Является ли число 6 решением неравенства 2х ≥ 10 3. Является неравенство 8х+4 ≥ 12 строгим 4. Соответствует ли неравенство -1 ≤ х ≤ 6 промежутку (-1;6) 5. Соответствует ли промежуток (12, +∞) неравенству х ≤ 12  6. Соответствует ли промежуток (11;77) изображению 6. Соответствует ли промежуток (11;77) изображению 7. Соответствует ли изображение промежутку Х ≤ 9 7. Соответствует ли изображение промежутку Х ≤ 98. Число 12 является наибольшим целым числом неравенства х ≥ 12 Один вопрос считается 1балл. Всего 8балл. 8. Домашнее задание: §5. № 121; 123 (Слайд 17) 9. Рефлексия. Цель: провести самооценку деятельности, выявить затруднения, наметить путь на устранения. (Слайд 18, 19)
Рабочий лист. __________________________ Карточка № 1. 1) 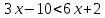 2) 2) 
Самостоятельная работа (Верно-1, неверно - 0) 1 вариант Является ли число -5 решением неравенства 2х ≥ 10 Является ли число 6 решением неравенства 2х ≥ 10 Является неравенство 2х+8 ≥ 3 строгим Соответствует ли неравенство -2 ≤ х ≤ 5 промежутку (-2;5) Соответствует ли промежуток (5, +∞) неравенству х ≤ 5 Соответствует ли промежуток (1;7) изображению  7. Соответствует ли изображение промежутку Х ≤ 10  8. Число 8 является наибольшим целым числом неравенства х ≥ 8
2 вариант 1. Является ли число -3 решением неравенства 3х ≥ 9 2. Является ли число 6 решением неравенства 2х ≥ 10 3. Является неравенство 8х+4 ≥ 12 строгим 4. Соответствует ли неравенство -1 ≤ х ≤ 6 промежутку (-1;6) 5. Соответствует ли промежуток (12, +∞) неравенству х ≤ 12  6. Соответствует ли промежуток (11;77) изображению 6. Соответствует ли промежуток (11;77) изображению 7. Соответствует ли изображение промежутку Х ≤ 9 7. Соответствует ли изображение промежутку Х ≤ 98. Число 12 является наибольшим целым числом неравенства х ≥ 12
|
