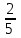теоия игр45. Решение Матрицей моделируется игра партнеровАиВ интересы которых противоположны
 Скачать 89.12 Kb. Скачать 89.12 Kb.
|
|
6) Для следующих платежных матриц определить нижнюю и верхнюю цены игры, наличие седловых точек, минимаксные стратегии. 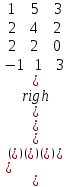 Решение: Матрицей моделируется игра партнеров А и В интересы которых противоположны. Игрок А имеет четыре стратегии: А1, А2, А3, А4. В распоряжении игрока В три стратегии В1,В2,В3. Найдем нижнюю цену игры: 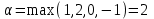 Найдем верхнюю цену игры: 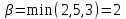 Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 2, которая указывает на максимальную чистую стратегию A2. Верхняя цена игры b = min(bj) = 2. Седловая точка (2, 1) указывает решение на пару альтернатив (A2,B1). Цена игры равна 2. 18) Решить аналитическим методом в смешанных стратегиях игру 2 × 2. Решение проиллюстрировать графически. 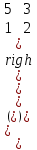 Решение: 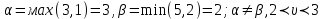 Игра не имеет седловой точки. Оптимальное решение будем искать в области смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегиям второго игрока. Левая и правая вертикальные линии на рисунке 1 соответствуют первой и второй стратегиям игрока А. На них отложены величины, равные значениям элементов платежной матрицы для стратегий игрока В.  В2=3 В1=1 В2=2 В1=5 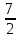 х2 х1 По формулам: 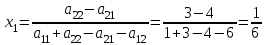 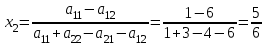 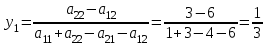 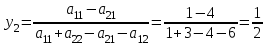 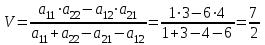 Находим оптимальные смешанные стратегии и цену игры: 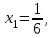 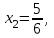 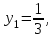 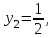 V= V=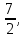 Ответ: оптимальные смешанные стратегии 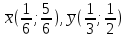 , цена игры составляет V= , цена игры составляет V=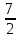 Данный ответ означает следующее: - если 1 игрок с вероятностью 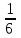 будет применять 1 стратегию и с вероятностью будет применять 1 стратегию и с вероятностью 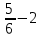 , то при достаточно большом кол-ве игр с данной матрицей его выигрыш составляет в среднем не менее , то при достаточно большом кол-ве игр с данной матрицей его выигрыш составляет в среднем не менее 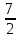 . .- если 2 игрок с вероятностью 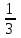 будет применять 1 стратегию и с вероятностью будет применять 1 стратегию и с вероятностью 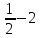 , то при достаточно большом количестве игр с данной матрицей его проигрыш составит в среднем не более , то при достаточно большом количестве игр с данной матрицей его проигрыш составит в среднем не более 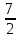 . .21. Найти графическим методом решение матричной игры. 21. 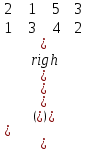 Решение: 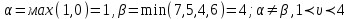 Игра не имеет седловой точки. Оптимальное решение будем искать в областях смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегиям второго игрока.
Выделяем нижнюю границу выигрыша B2КB3. Максиминной оптимальной стратегии игрока A соответствует точка К, лежащая на пересечении прямых B2B2 и B3B3, для которых можно записать следующую систему уравнений: y = 1 + (5 - 1)p2 y = 4 + (1 - 4)p2 Откуда p1 = 4/7 p2 = 3/7 Цена игры, y = 19/7 Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию B1, которая дает явно больший проигрыш игроку B, и, следовательно, q1 = 0. q2+4q3 = y 5q2+q3 = y q2+q3 = 1 или q2+4q3 = 19/7 5q2+q3 = 19/7 q2+q3 = 1 Решая эту систему, находим: q2 = 3/7. q3 = 4/7. Ответ: Цена игры: y = 19/7, векторы стратегии игроков: Q(0, 3/7, 4/7), P(4/7, 3/7). 33) Решить задачу симплекс-методом. (В облегченном варианте достаточно свести задачу матричной игры к построению первой симплекс-таблицы). 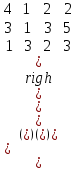 Решение: 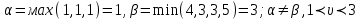 Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий. Для определения оптимальной стратегии игрока А имеем следующую задачу линейного программирования: 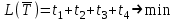 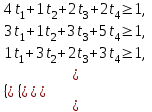 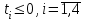 Начальная симплекс-таблица
достигается в точке с координатами: 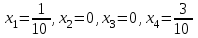 , , 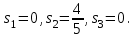 Для нахождения оптимальной стратегии игрока В имеем следующую задачу линейного программирования: 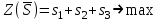 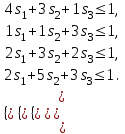 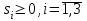 Начальная симплекс-таблица
достигается в точке с координатами: 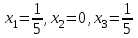 , , 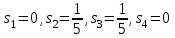 . .Задача 50. Решить задачу игры с природой, проведя соответствующее моделирование условий. Решить игру с природой по критерию Гурвица, α=0,5 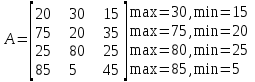 Решение: 1. Для матрицы выигрышей: К(А1)=0,5∙30+0,5∙(15)=22,5 К(А2)=0,5∙75+0,5∙(20)=47,5 К(А3)=0,5∙80+0,5∙(25)=52,5 К(А4)=0,5∙85+0,5∙(5)=45 Лучшая стратегия А3. 2. Для матрицы потерь: К(А1)=0,5∙15+0,5∙30=22,5 К(А2)=0,5∙20+0,5∙75=47,5 К(А3)=0,5∙25+0,5∙80=52,5 К(А4)=0,5∙5+0,5∙85=45 Лучшая стратегия А3. Список используемой литературы 1.Дубина И.Н. Основы теории экономических игр: учебное пособие для вузов / И.Н. Дубина. – М.: КноРус, 2010. – 208 с. 2. Методология и технология имитационных исследований слож-ных систем: современное состояние и перспективы развития: Мо-ногр./ В.В. Девятков - М.: Вуз. учеб.: ИНФРА-М, 2013. - 448 с. - (ЭБС.znanium.com) 3. Количественные методы в экономических исследованиях : учеб-ник для вузов /под ред. .М.В.Грачевой,Ю.Н.Черемных,Е.А.Тумановой. - 2-е изд.,перераб.и доп. - М. : ЮНИТИ, 2013. - 687с. 4. Тихомиров Н.П. Риск-анализ в экономике / Н.П. Тихомиров. − М.: Экономика, 2010. – 318 с. 5. Ларичев О.И. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: учебник для вузов / О.И. Ларичев. – М.: Логос, 2008. – 391 с. 6. Экономико-математические методы и модели. Задачник: учебно-практическое пособие / под ред. С.И. Макарова, С.А. Севостьяновой. − 2-е изд., перераб. − М.: КНОРУС, 2009. − 208 с. |

 В1=7
В1=7 В4=6
В4=6
 В3=4
В3=4 К
К