Решение. Меньший конус подобен большему с коэффициентом 0 Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса
 Скачать 408.25 Kb. Скачать 408.25 Kb.
|
|
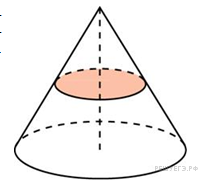
Решение.Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса. Ответ: 2. Ответ: 2 27052 2 1. Решение. По теореме Пифагора найдем, что радиус основания равен Ответ: 128. Ответ: 128 27120 128 Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.(слайд №20)  С .
2. Решение. В треугольнике, образованном радиусом основания r, высотой h и образующей конуса l, углы при образующей равны, поэтому высота конуса равна радиусу его основания: h = r. Тогда объем конуса, деленный на Ответ: 9. Ответ: 9 27121 9 Решение. Треугольник ABC — так же равнобедренный, т. к. углы при основании Ответ: 72. Ответ: 72 27122 72 Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на
3. Решение. Радиус основания конуса r равен половине диагонали квадрата ABCD: Ответ: 16. Ответ: 16 27123 16 Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса. .(слайд №22)
4.Решение. Площадь боковой поверхности конуса равна Ответ: 3. Ответ: 3 27135 3 Решение. Площадь боковой поверхности конуса равна Ответ: 1,5. Ответ: 1,5 27137 1,5 Решение. Площадь поверхности складывается из площади основания Радиус основания найдем по теореме Пифагора для треугольника, образованного высотой, образующей и радиусом: Ответ: 144. Ответ: 144 27159 144 Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. .(слайд №23)
5.Решение. Площадь основания конуса равна Значит, в прямоугольном треугольнике, образованном высотой, образующей и радиусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Следовательно, угол между образующей конуса и плоскостью основания равен 60°. Ответ: 60. Ответ: 60 27160 60 Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса. .(слайд №24)
6. Решение. Исходный и отсеченный конус подобны с коэффициентом подобия 2. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия. Поэтому площадь отсеченного конуса в 4 раза меньше площади поверхности исходного. Тем самым, она равна 3. Ответ: 3. Ответ: 3 27161 3 Решение. Найдем образующую по теореме Пифагора: Ответ: 24. Ответ: 24 27167 24 Найдите объем
7. Решение. Объем данной части конуса равен Ответ: 87,75. Ответ: 87,75 27202 87,75 Найдите объем
8.Решение. Объем данной части конуса равен Ответ: 243. Ответ: 243 27203 243 Решение. 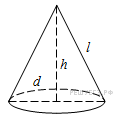 Рассмотрим осевое сечение конуса. По теореме Пифагора Рассмотрим осевое сечение конуса. По теореме Пифагора 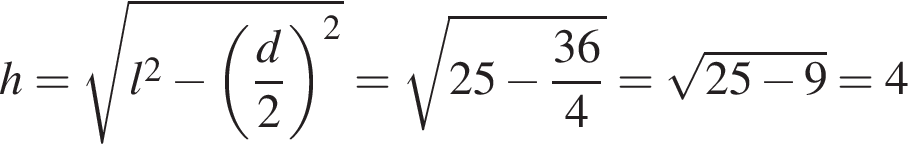 . .Ответ: 4. Ответ: 4 284360 4 В сосуде, имеющем форму конуса, уровень жидкости достигает
Решение. Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем большего конуса в 8 раз больше объема меньшего конуса, он равен 560 мл. Следовательно, необходимо долить 560 − 70 = 490 мл жидкости. Ответ: 490. Ответ: 490 318145 490 9.Решение. 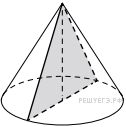 Осевым сечением конуса является равнобедренный треугольник, основание которого — диаметр основания конуса, а высота совпадает с высотой конуса. Образующая конуса Осевым сечением конуса является равнобедренный треугольник, основание которого — диаметр основания конуса, а высота совпадает с высотой конуса. Образующая конуса Ответ: 48. Ответ: 48 324456 48 Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна
10. Конусообразная палатка высотой 3,5 м и диаметром основания 4 м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку? .(слайд №29) Решение. Образующая конуса 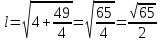 , что примерно составляет 8,06 м. Тогда площадь боковой поверхности конуса равна , что примерно составляет 8,06 м. Тогда площадь боковой поверхности конуса равна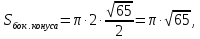 что примерно составляет 5,3 м2. На палатку пошло примерно 25,3 м2 парусины. что примерно составляет 5,3 м2. На палатку пошло примерно 25,3 м2 парусины.Ответ: 25,3 м2 |



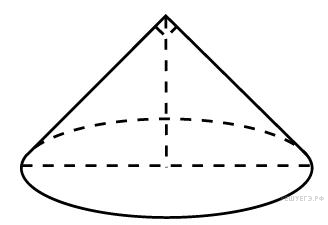
 9π•3=9π(см3) Ответ: 9
9π•3=9π(см3) Ответ: 9
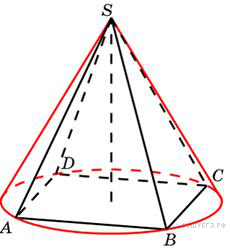
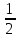 АС, АС=4
АС, АС=4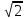 , значит, R=2
, значит, R=2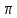 R=6 → R=
R=6 → R=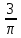



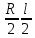 +π
+π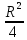 =
=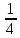 (πRl+πR2) =
(πRl+πR2) =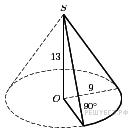
 92
92 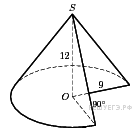
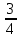 V.
V.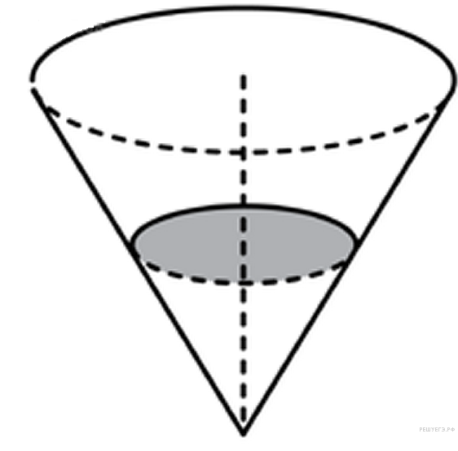
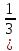 πr2h) • 8=70
πr2h) • 8=70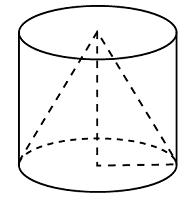
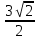
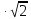 = πR2
= πR2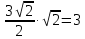 .
.