практ. рейтинговая работа 2022 По Математике 2. Решение методом Гаусса

• Название: Решение методом Гаусса
• Анкор: практ
• Дата: 25.12.2022
• Размер: 186.44 Kb.
• Имя файла: рейтинговая работа 2022 По Математике 2.docx
• Тип: Решение; #863523

Кафедра математических и естественно-научных дисциплин


Рейтинговая работа ___По Математике______________

(домашняя творческая работа, расчетно-аналитическое задание, реферат, контрольная работа)

по дисциплине ____ Математике
Задание/вариант № _____2_______

Тема* ______________________________________________________________

Выполнена обучающимся группы ___Галкина Ирина Николаевна_____

(фамилия, имя, отчество)
Преподаватель ____________________________________________________

(фамилия, имя, отчество)

Москва – 2021 г.

2. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РЕЙТИНГОВОЙ РАБОТЫ

(1 семестр).

1) Даны матрицы и число . Найти матрицу .
2). ,
Умножение матриц: строки первой матрицы умножаются на столбцы второй.
AB=


qC=
= + =


2) Дана система линейных алгебраических уравнений

Найти решение этой системы любым методом.
2).
Решение методом Гаусса

Приведем расширенную матрицу системы к ступенчатому виду: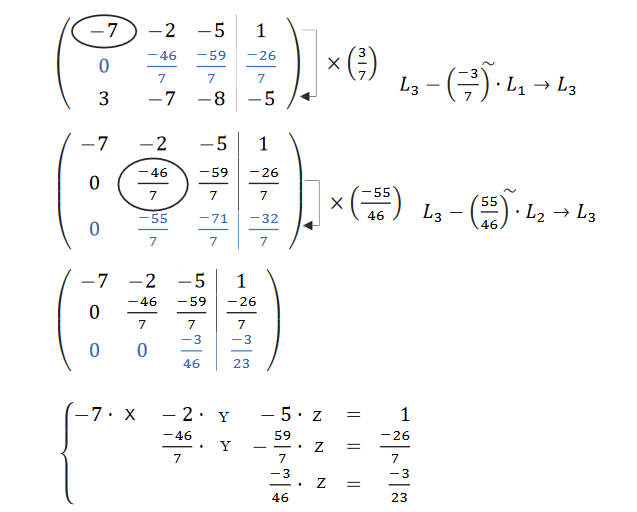



Из уравнения 3 системы найдем переменную Z: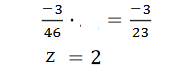



Из уравнения 2 системы найдем переменную Y: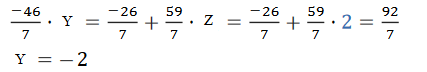



Из уравнения 1 системы (1) найдем переменную X: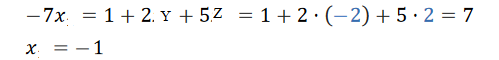

Ответ: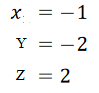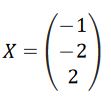


3) Известны координаты (см. таблицу 1) в прямоугольной системе координат трех точек , являющихся вершинами треугольника. Изобразить треугольник в этой прямоугольной системе координат и найти:

3.1 координаты векторов , и их длины;

3.2 Координаты векторов.

Координаты векторов находим по формуле:

X = xj - xi; Y = yj - yi

здесь X,Y координаты вектора; xi, yi - координаты точки Аi; xj, yj - координаты точки Аj

Например, для вектора AB

X = x2 - x1; Y = y2 - y1

X = 14-(-3) = 17; Y = 4-(-2) = 6

AB(17;6)


AC(9;10)

BC(-8;4)

3.2 скалярное произведение векторов , и угол между векторами , ;

3.3 скалярное произведение векторов ,




3.4 Угол между прямыми
Найдем угол A как угол между двумя прямыми.
Уравнение прямой AB:y = ⁶/₁₇x ^-16/₁₇
Уравнение прямой AC:y = ¹⁰/₉x + ⁴/₃
Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k₁x + b₁ и y₂ = k₂x + b₂, вычисляется по формуле:

Угловые коэффициенты данных прямых равны ⁶/₁₇ и ¹⁰/₉. Воспользуемся формулой, причем ее правую часть берем по модулю: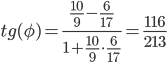

tg(φ)=¹¹⁶/₂₁₃
φ = arctg(¹¹⁶/₂₁₃) = 28.57⁰

3.5 векторное произведение векторов , и площадь треугольника ;

3.7 Длина сторон треугольника.
Расстояние d между точками M₁(x₁; y₁) и M₂(x₂; y₂) определяется по формуле:




3.8 Площадь треугольника
Пусть точки A₁(x₁; y₁), A₂(x₂; y₂), A₃(x₃; y₃) - вершины треугольника, тогда его площадь выражается формулой:
S=1/2


В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:
= =-9*(-4) - 8*(-10) = 116

По формуле получаем:


3.4 значение параметра , при котором векторы и будут коллинеарны;

3.5 координаты точки , делящей отрезок в отношении ;

3.5.1 Деление отрезка в данном отношении.
Координаты точки , делящий отрезок AB в отношении AP:PB = m₁:m₂,=1/2 определяется формулой:

Координаты точки P находятся по формулам:


2,67


3.6 каноническое уравнение стороны ;

Уравнение прямой
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями:

Уравнение прямой AB
Каноническое уравнение прямой:

или

или
y = ⁶/₁₇x ^-16/₁₇ или 17y -6x +16 = 0

3.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку параллельно прямой ;

Уравнение параллельной прямой AB, проходящей через точку С
Уравнение прямой AB: y = ⁶/₁₇x ^-16/₁₇
Уравнение СN параллельно AB находится по формуле:
y - y₀ = с(x - x₀)
Подставляя x₀ = 0, с = ⁶/₁₇, y₀ = 0 получим:
y-0 = ⁶/₁₇(x-0)
или
y = ⁶/₁₇x или 17y -6x - 0 = 0

Таблица 1

Номер варианта	Координаты точек
2

4)Известны координаты (см. таблицу 2) в прямоугольной системе координат вершин пирамиды .

4.1найти смешанное произведение векторов и объем пирамиды ;

4.1.1 Координаты векторов.
Координаты векторов находим по формуле:
X = x_j - x_i; Y = y_j - y_i; Z = z_j - z_i
здесь X,Y,Z координаты вектора; x_i, y_i, z_i - координаты точки А_i; x_j, y_j, z_j - координаты точки А_j;
Например, для вектора A₁A₂
X = x₂ - x₁; Y = y₂ - y₁; Z = z₂ - z₁
X = -1-3; Y = 0-(-1); Z = 1-2
A₁A₂(-4;1;-1)
A₁A₃(-2;8;1)
A₁A₄(5;6;6)
A₂A₃(2;7;2)
A₂A₄(9;5;7)
A₃A₄(7;-2;5)
4.1.2 Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:




4.1.3 Объем пирамиды.
Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен:

X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3

-4 1 -1 -2 8 1 5 6 6

где определитель матрицы равен:
∆ = (-4)*(8*6-6*1)-(-2)*(1*6-6*(-1))+5*(1*1-8*(-1)) = -99
7) Уравнение прямой
Прямая, проходящая через точки A₁(x₁; y₁; z₁) и A₂(x₂; y₂; z₂), представляется уравнениями:

Параметрическое уравнение прямой:
x=x₀+lt
y=y₀+mt
z=z₀+nt
Уравнение прямой A₁A₂(-4,1,-1)

Параметрическое уравнение прямой:
x=3-4t
y=-1+t
z=2-t
Уравнение прямой A₁A₃(-2,8,1)

Параметрическое уравнение прямой:
x=3-2t
y=-1+8t
z=2+t
Уравнение прямой A₁A₄(5,6,6)

Параметрическое уравнение прямой:
x=3+5t
y=-1+6t
z=2+6t

4.2 найти каноническое уравнение прямой ;

Воспользуемся формулой канонического уравнения прямой: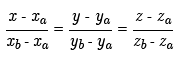



Подставим в формулу координаты точек: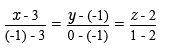



В итоге получено каноническое уравнение прямой: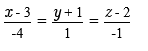



4.3найти общее уравнение плоскости ;

Уравнение плоскости.
Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃

x-3	y+1	z-2

(x-3)(1·1-8·(-1)) - (y+1)((-4)·1-(-2)·(-1)) + (z-2)((-4)·8-(-2)·1) = 9x + 6y - 30z + 39 = 0
Упростим выражение: 3x + 2y - 10z + 13 = 0

Таблица 2

Номер варианта	Координаты точек
2