Статистика. МУ им.Витте РР Статистика Вар. 12. Задания для выполнения рейтинговой работы 3 Выполнение задания 3
 Скачать 314 Kb.
|
|
Титульный лист Статистика Рейтинговая работа Вариант 12 Содержание Задания для выполнения рейтинговой работы 3 Выполнение задания 3 Список использованных источников 17 Задания для выполнения рейтинговой работы1. Скопировать данные своего варианта. 2. Ранжировать ряд данных сортировкой по значениям от минимального к максимальному. 3. Рассчитать количество интервалов по формуле Стерджеса, округлив вверх до целых единиц. 4. Рассчитать величину интервала h, округлить до десятков. 5. Рассчитать границы интервалов: 6. Подсчитать количество единиц совокупности, принадлежащих каждому из интервалов. 7. Построить интервальный вариационный ряд в виде таблицы 8. Построить гистограмму распределения для интервалов и полигон распределения для вариант, кумуляту. 9. Вычислить среднее арифметическое, моду, медиану, квартили, децили. 10. Вычислить показатели вариации: R, dср, s2, s, Vr, Vd ,V. Вычислить асимметрию и эксцесс. 11. Сделать вывод об однородности вариационного ряда, о симметричности и остро- или плоско-вершинности распределения. Выполнение задания1. Скопируем исходные данные Исходные данные приведены в таблице 1. Таблица 1 - Исходные данные для 12-го варианта
2. Ранжировать ряд данных сортировкой Ранжированный ряд представлен в таблице 2. Таблица 2 - Ранжированные данные
Число наблюдений п = 59. 3. Рассчитаем количество интервалов по формуле Стерджеса: k= 1 + 3,322 × lg n = 1 + 3,322 × lg 59 = 6,883 Округляем вверх до целых единиц. Таким образом, будем строить ряд, образовав 7 групп с равными интервалами. 4. Определим величину интервала При построении интервального ряда с равными интервалами величина интервала h определяется по формуле:  , гдехmax и хmin – наибольшее и наименьшее значения признака в исследуемой совокупности; k- число групп интервального ряда. Расчет величины интервалов:  Округляя до десятков, получаем h = 30. 5. Рассчитаем границы интервалов Путем последовательного прибавления величины интервала h = 30 к нижней границе, получаем следующие границы интервалов ряда распределения: До 30 60 - 90 90 - 120 120 - 150 150 - 180 180 - 210 210 и более 6,7. Рассчитаем частоты групп и получим интервальный ряд распределения Определяем число единиц, входящих в каждую группу, используя принцип полуоткрытого интервала [ ), согласно которому единицы со значениями признаков, которые служат одновременно верхними и нижними границами смежных интервалов, будем относить ко второму из смежных интервалов. Помимо количества единиц в абсолютном выражении (частот) в таблице 4 рассчитываем относительные частоты (частости) по формуле: 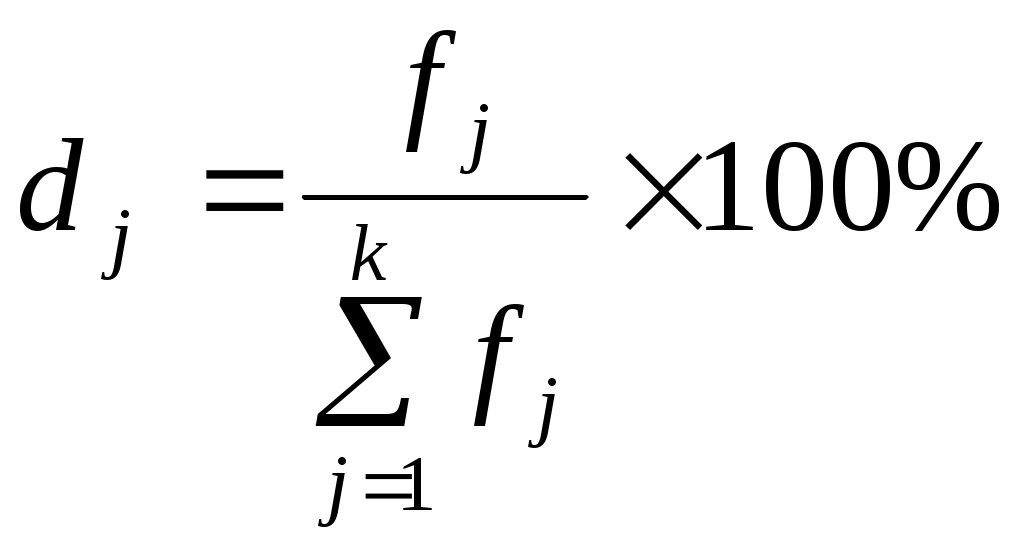 .Таблица 3 - Интервальный ряд распределения
Вывод. Распределение наблюдений по группам не является полностью равномерным. Преобладают наблюдения со значениями признака от 60 до 90 единиц. Это 16 наблюдений, доля которых составляет 27,01% от общего числа наблюдений. Самая малочисленная группа с наибольшим значением признака (свыше 210 единиц). В данную группу попадает 5,1% от общего числа наблюдений (3 единицы). 8. Построим графики ряда распределения Гистограмма – столбиковая диаграмма, она позволяет визуально оценит симметричность распределения, его близость к нормальному. Для построения полигона в прямоугольной системе координат на оси абсцисс откладывают значения интервалов, а на оси ординат - значения частот или относительных частотГистограмма строится по 1-му и 2-му столбцу таблицы 3 и представлена на рисунке 1. 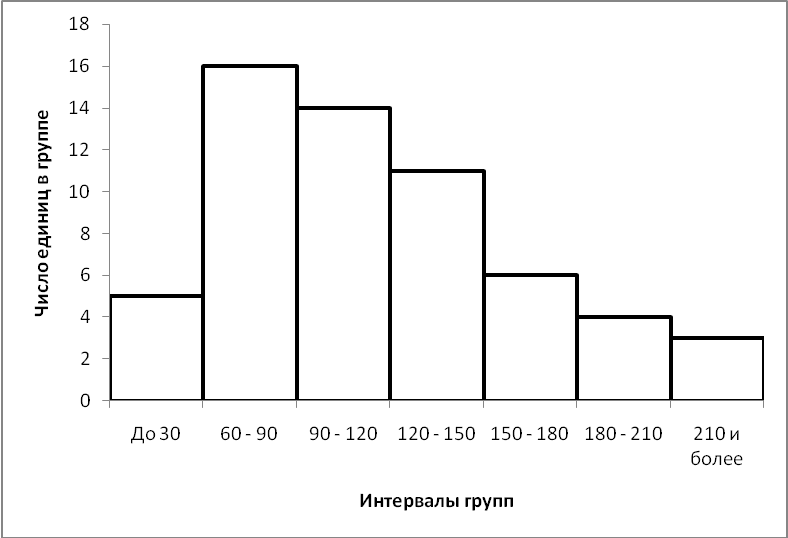 Рисунок 1 – Гистограмма распределения Полигон чаще используют для изображения дискретных рядов. Для построения полигона в прямоугольной системе координат на оси абсцисс откладывают значения аргумента, т. е. варианты, а на оси ординат - значения частот или относительных частот. Далее в этой системе координат строят точки, координатами которых являются пары соответствующих чисел из вариационного ряда. Полученные точки последовательно соединяют отрезками прямой. Крайнюю «левую» точку соединяют с точкой оси абсцисс, абсцисса которой находится слева от рассматриваемой точки на таком же расстоянии, как абсцисса ближайшей справа точки. Аналогично крайнюю «правую» точку также соединяют с точкой оси абсцисс. Для интервального ряда в качестве значений признака принимаем середины интервалов. Середину интервала находим как среднюю арифметическую из нижней и верхней границ интервалов:  Расчет представлен в таблице 4. Таким образом, полигон строим по 2-му и 3-му столбцу таблицы 4. 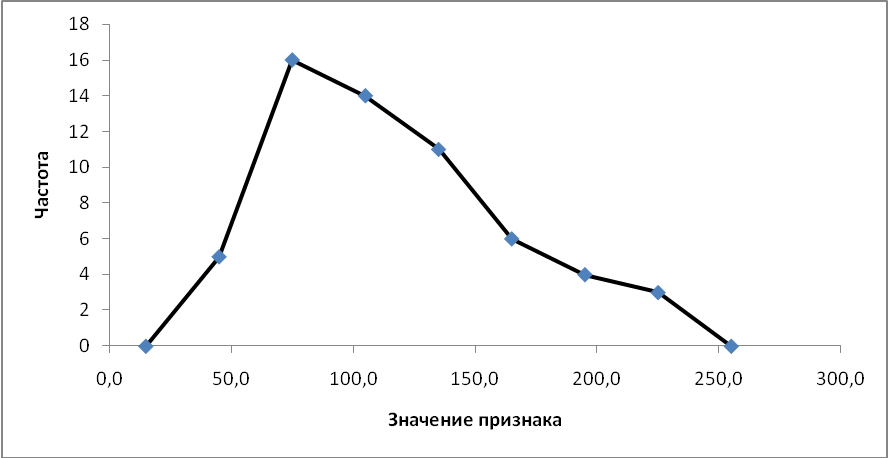 Рисунок 2 – Полигон распределения Кумулята строится по накопленным частотам (расчет представлен в таблице 4). Она начинается с нижней границы 1-го интервала (30), накопленная частота откладывается в верхней границе интервала: 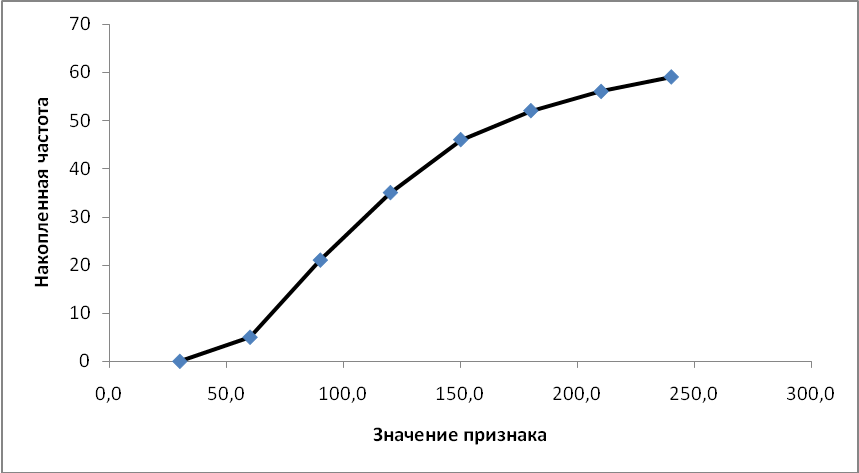 Рисунок 3 – Кумулята распределения 9. Вычислим среднее арифметическое, моду, медиану, квартили, децили Для расчета показателей строим вспомогательную таблицу 4. Таблица 4 - Вспомогательная таблица для расчета показателей вариации и центра распределения
Для расчета среднего в интервальном ряду используется формула средней арифметической взвешенной: 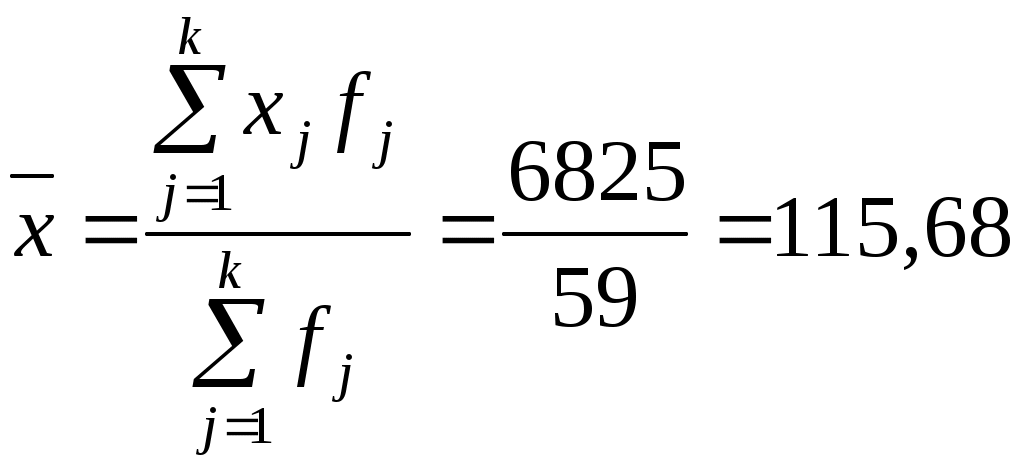 Вывод. В рассматриваемой совокупности среднее значение признака составляет 115,68 единицы. Мода и медиана являются структурными средними величинами, характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку. Мода Мо – значение признака, которое встречается наиболее часто в рассматриваемой совокупности. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту). Конкретное значение моды для интервального ряда рассчитывается по формуле:  , гдехМo – нижняя граница модального интервала, h – величина модального интервала, fMo– частота модального интервала, fMo-1 – частота интервала, предшествующего модальному, fMo+1 – частота интервала, следующего за модальным. Согласно данным модальным интервалом ряда является интервал 60-90, так как его частота максимальна (f1= 16). Расчет моды:  85,38Вывод. Для рассматриваемой совокупности наиболее часто встречаются значения признака равные 85,38 единиц. Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности. Конкретное значение медианы для интервального ряда рассчитывается по формуле: 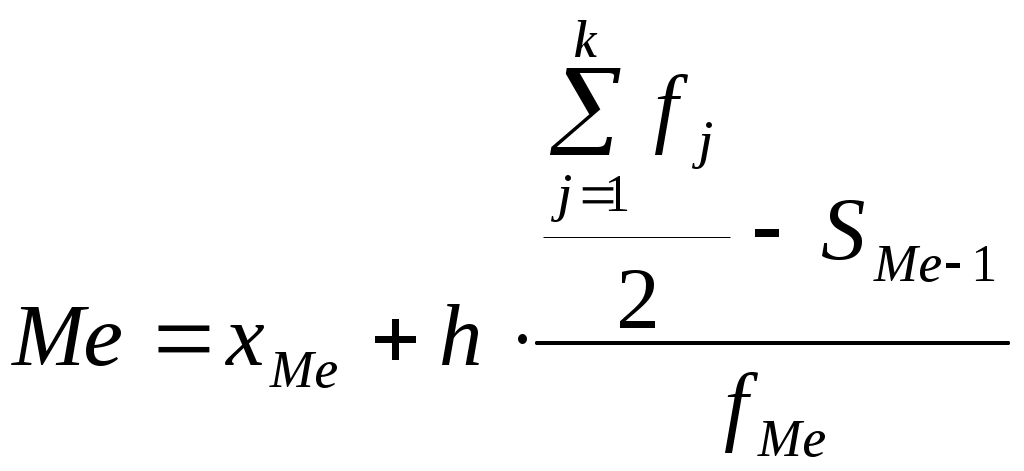 , где – нижняя граница медианного интервала,h – величина медианного интервала;  – сумма всех частот ряда; – частота медианного интервала; – сумма частот, накопившихся до начала медианного интервала.Медианным интервалом является интервал 90-120, так как именно в этом интервале накопленная частота S3 =35 впервые превышает величину, равную половине совокупности (0,5·59 = 29,5). Расчет медианы: 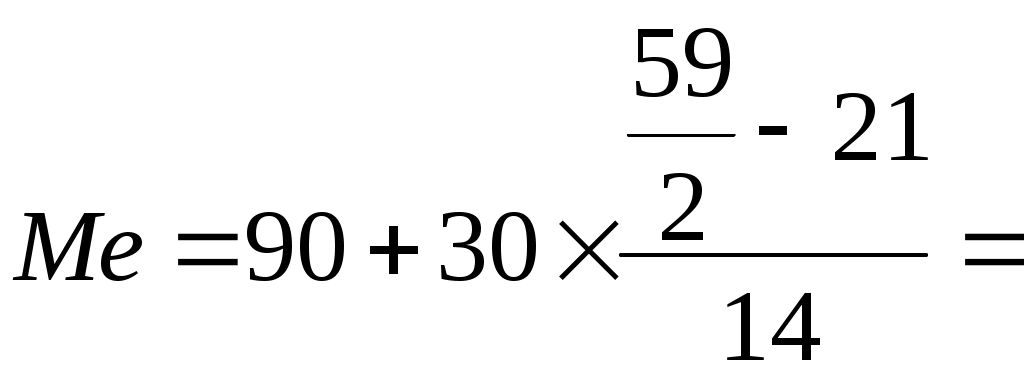 108,21Вывод. В рассматриваемой совокупности половина значение признак не менее 108,21 единиц, а другая половина – не более 108,21 единиц.  , следовательно, асимметрия правосторонняя, гистограмма сдвинута от центра влево. В совокупности преобладают единицы с более низкими значениями признака, чем среднее значение.Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1и Q2; 25% - между Q2и Q3; остальные 25% превосходят Q3. 0-й квартиль – минимальное значение признака; 2-й квартиль – медиана; 1-й и 3-й квартиль рассчитываются аналогично медиане. Значение Q1 будет находиться в интервале 60-90, т.к. именно в этом интервале накопленная частота равна 21 впервые превышает четверть суммы частот 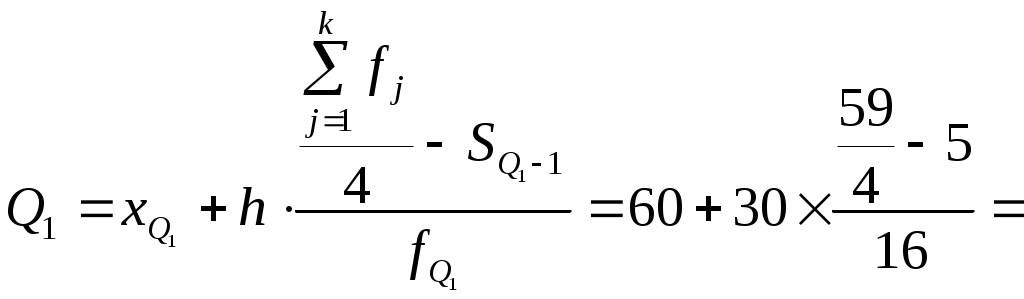 . 78,28 Значение Q3 будет находиться в интервале 120-150, т.к. именно в этом интервале накопленная частота 46 впервые превышает три четверти суммы частот 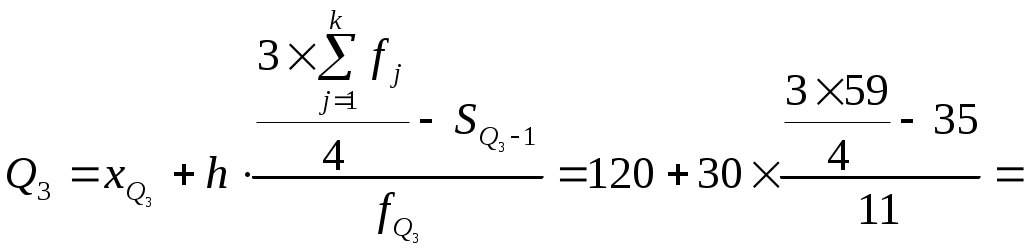 . 145,23Децили делят совокупность на 10 равных частей. Рассчитываются аналогично медиане и квартилям. Интервалом 1-го дециля d1 будет является интервал 60-90, т.к. именно в этом интервале накопленная частота 21 впервые превышает 1/10 суммы частот 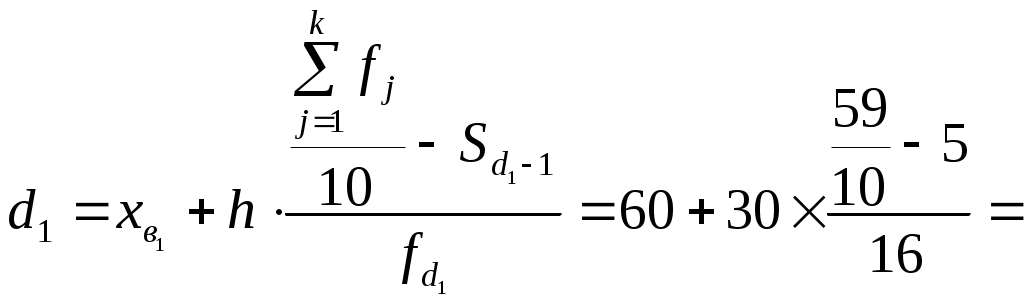 . 61,69Интервалом 9-го дециля d9 будет интервал 180-210, т.к. в этом интервале накопленная частота 56 впервые превышает 9/10 суммы частот 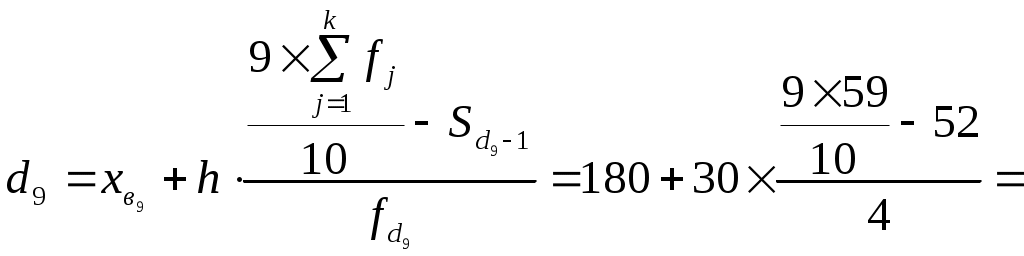 . 188,25 10. Вычислим показатели вариации Вспомогательные расчеты приведены в таблице 5. Размах вариации характеризует амплитуду колебаний значений признака, рассчитывается как разность максимального и минимального значения признака. Рассчитываем размах по исходным данным:  256 – 32 = 224Среднее линейное отклонение показывает, насколько в среднем отклоняются конкретные варианты признака от среднего значения. Для сгруппированных данных рассчитываем взвешенное среднее линейное отклонение: 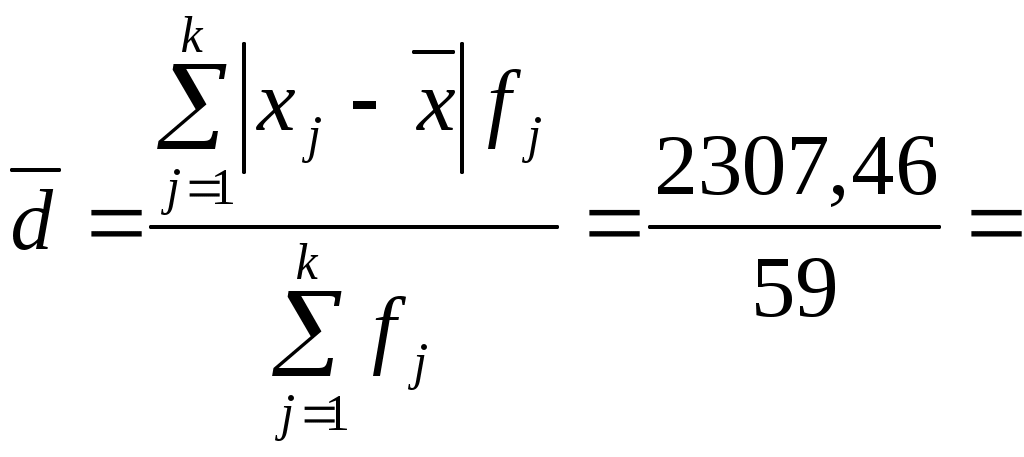 38,46Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. Для интервального ряда используется формула взвешенной дисперсии: 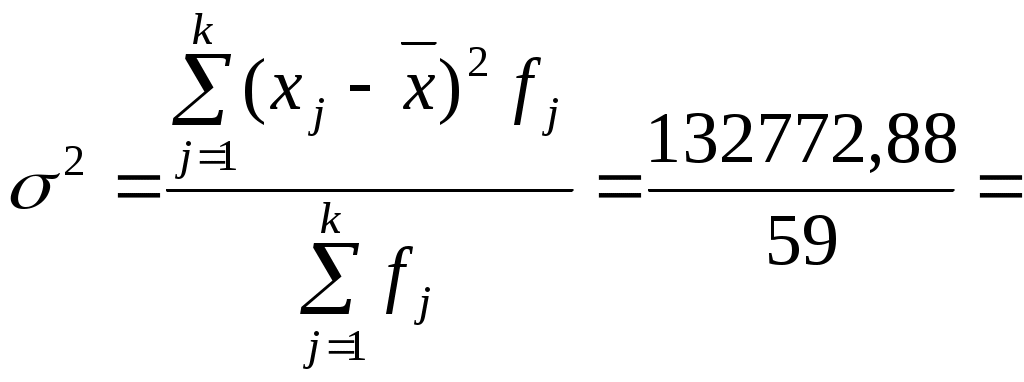 2212,88Среднее квадратическое отклонение также как и среднее линейное отклонение показывает, насколько в среднем отклоняются конкретные варианты признака от среднего значения. Однако является более точной характеристикой. Рассчитывается, как корень квадратный из дисперсии:  47,04Расчет исправленной (скорректированной) дисперсии:  2212,88×59/58 = 2249,76Расчет исправленного (скорректированного) среднего квадратического отклонения:  47,43Вывод. Отклонение от среднего значения признака в ту или иную сторону составляет 47,43 единиц. Наиболее характерные значения признака в рассматриваемой совокупности находятся в пределах от 68,25 до 163,11 (диапазон  ).Коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности:  41,0%Вывод. Значение коэффициента вариации превышает 40%, следовательно, вариация признака в исследуемой совокупности единиц умеренная и совокупность не является однородной. Найденное среднее значение признака не является типичной и надежной характеристикой среднего. Относительное линейное отклонение  33,2%Коэффициент осцилляции по сгруппированным данным:  = 193,6%Вывод. Доля среднего линейного отклонения в среднем значении признака составляет 33,2%. Доля размаха вариации в среднем значении – 193,6%. 11. Рассчитаем показатели формы распределения К показателям формы распределения относятся коэффициент асимметрии и эксцесса. Для расчета показателей формы распределения строим вспомогательную таблицу 5. Рассчитываем центральный момент третьего порядка: 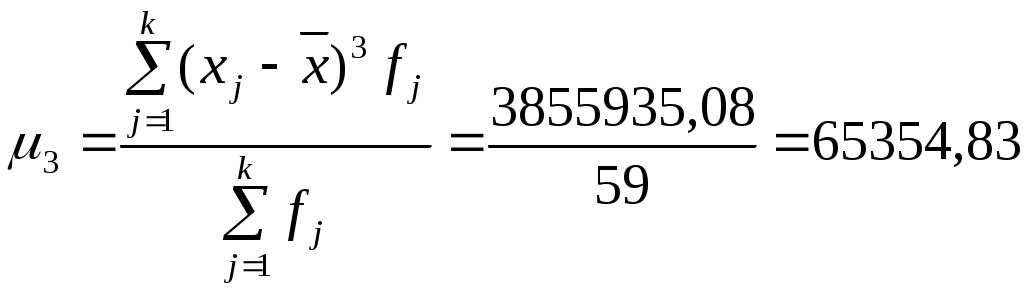 Таблица 5 - Вспомогательная таблица для расчета показателей формы распределения
Расчет коэффициента асимметрии:  0,612Вывод. Значение коэффициента асимметрии положительное, что свидетельствует о правосторонней асимметрии распределения, т.е. в совокупности преобладают единицы со значением признака меньшие, чем среднее. Рассчитываем центральный момент четвертого порядка: 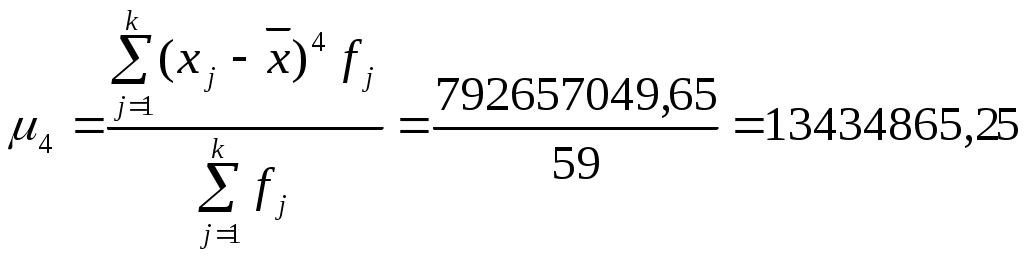 Расчет коэффициента эксцесса:  -0,346Вывод. Показатель эксцесса отрицательный, т.е. вершина кривой распределения лежит ниже вершины кривой нормального закона распределения, а форма кривой более пологая по сравнению с кривой нормального закона. Это означает, что значения признака не концентрируются в центральной части ряда, а рассеяны по всему диапазону. Список использованных источниковБережной В. И. Статистика в примерах и задачах [Электронный ресурс]: учебное пособие / В.И. Бережной, О.Б. Бигдай, О.В. Бережная, Киселева О.А. - М.: НИЦ ИНФРА-М, 2016. - 288 с.– Режим доступа: http://znanium.com/bookread2.php?book=502176 Глинский, В. В. Статистика: учебник / В.В. Глинский, В.Г. Ионин, Л.К. Серга [и др.] ; под ред. В.Г. Ионина. — 4-е изд., перераб. и доп. — М. : ИНФРА-М, 2017. — 355 с. – Режим доступа: http://znanium.com/bookread2.php?book=552459 Гужова, О.А. Статистика в управлении социально-экономическими процессами : учеб. пособие / О.А. Гужова, Ю.А. Токарев. — М. : ИНФРА-М, 2017. — 172 с. — Режим доступа: http://znanium.com/bookread2.php?book=556718 Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики/ [Текст] Учебник. – М.: ИНФРА – М, 2015. – 416 с. Рудакова Р.П., Букин Л.Л., Гаврилов В.И. Статистика. [Текст] 2-е изд. – сПб.: Питер, 2017. – 288 с.: ил. |
