контрольная. математика. Решение n 4 p 0,5 q 1 p 1 0,5 0,5
 Скачать 136.82 Kb. Скачать 136.82 Kb.
|
1 2 Решение Результаты тестирования можно представить в виде `х ±mх , и `y±my где `х и`y - выборочные средние, m`х и m`у – статистические ошибки выборочных средних. Группа Х: 87,7 ± 2,564 Простая средняя арифметическая Стандартная ошибка выборки для среднего: Стандартная ошибка среднего указывает, на сколько среднее выборки 87.7 отличается от среднего генеральной совокупности. Предельная ошибка выборки: или ε = tkp sc = 2.685*0.955 = 2.564 Доверительный интервал: (87.7 - 2.564;87.7 + 2.564) = (85.136;90.264) С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала. Группа Y: 83,7 ± 2,436 Простая средняя арифметическая Стандартная ошибка выборки для среднего: Стандартная ошибка среднего указывает, на сколько среднее выборки 83.7 отличается от среднего генеральной совокупности. Предельная ошибка выборки: Доверительный интервал: (83.7 - 2.436;83.7 + 2.436) = (81.264;86.136) С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала. Проводим проверку гипотезы о равенстве генеральных средних (t-критерий Стьюдента): Альтернативная гипотеза формулируется в соответствии с условиями задачи или эксперимента: (критическая область – двусторонняя) Найдём экспериментальное значение критерия Стьюдента: = Число степеней свободы f = nх + nу – 2 = 10 + 10 – 2 = 18 Критическая область – двусторонняя: (-∞;-tkp)U(tkp;+∞). Определяем значение tkp по таблице распределения Стьюдента По таблице Стьюдента находим: Tтабл(n1+n2-2;α/2) = Tтабл(18;0.025) = 2.445 tkp = 2.445 Экспериментальное значение критерия T попало в критическую область T ≥ tkp, поэтому нулевую гипотезу следует отклонить в пользу альтернативной. Генеральные средние двух выборок не равны. Задание 5. Известны результаты тестирования в двух группах спортсменов, причем выборочные средние составляют `x и`у, а статистические ошибки выборочных средних mx и my. Определить, различаются ли генеральные средние, если численность групп составляет nx и ny человек, соответственно.
Решение: Результаты тестирования можно представить в виде `х ±mх , и `y±my где `х и`y - выборочные средние, m`х и m`у – статистические ошибки выборочных средних. Группа Х: 68,8 ± 2,8 (см) Группа Y: 75,5 ± 2,2 (см) 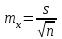 , тогда , тогда 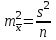 и и 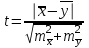 Вычислим эмпирическое значение t-критерия Стьюдента. 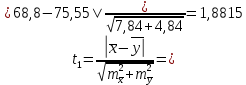 Количество степеней свободыn = 10+6-2 = 14. В этом случае критические значения t-критерия Стьюдента на уровнях значимости 0,05; 0,01; 0,001 составляют 2,1448; 2,9768; 4,1405, соответственно (приложение 3). Эмпирическое значение t-критерия составляет 1,8815, это больше чем t0,05 =2,1448, но меньше, чем t0,01=4,1405. Задание 6. Установить тесноту взаимосвязи между показателями Х и У при помощи коэффициента корреляции Браве-Пирсона.
Решение
Для вычисления коэффициента корреляции Браве-Пирсона составим расчетную таблицу, при помощи которой найдем выборочные средниеx,y, а также средние квадратические отклонения sxи sy.
Выборочные средние. sx2 = 22,8574/6 = 3.809524; sx =1.9518; sy2 = 31,42857/6 = 5.238095 sy= 2.28883 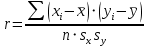 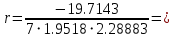 -0,63 -0,63Для определения достоверности взаимосвязи необходимо сравнить полученный выборочный коэффициент корреляции с критическим значением (находится в статистической таблице), которое зависит от объема выборки. При объеме выборки n = 7 критическое значение r0,05 = 0.75. Поскольку выборочное значение оказалось меньше критического, то нельзя утверждать, что между показателями Х и Y существует взаимосвязь. Задание 7. Установить тесноту взаимосвязи между показателями Х и У при помощи коэффициента корреляции Спирмена.
Решение Матрица рангов.
Проверка правильности составления матрицы на основе исчисления контрольной суммы: Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно. Поскольку среди значений признаков х и у встречается несколько одинаковых, т.е. образуются связанные ранги, то в таком случае коэффициент Спирмена вычисляется как: где j - номера связок по порядку для признака х; Аj - число одинаковых рангов в j-й связке по х; k - номера связок по порядку для признака у; Вk - число одинаковых рангов в k-й связке по у. A = [(33-3)]/12 = 2 B = [(23-2) + (23-2)]/12 = 1 D = A + B = 2 + 1 = 3 По таблице Стьюдента находим t(α/2, k) = (0.05/2;4) = 3.495 Поскольку Tkp > p, то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически - не значим и ранговая корреляционная связь между оценками по двум тестам незначимая. Задание 8. Изучалась динамика показателей физической подготовленности спортсменов контрольной и экспериментальной групп. В каждой группе дважды в течение годичного тренировочного цикла проведено тестирование. Найти абсолютные и относительные темпы прироста результатов тестирования. Решение
Решение: Найдем абсолютные и относительные приросты средних результатов спортсменов контрольной группы прыжок в высоту. Абсолютный прирост: Δпр = х2 – х1 = 46,8-42,8 = 4 см Относительный прирост: 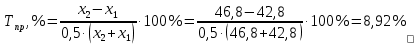 Найдем темпы роста результатов в беге на 100 м: Абсолютный прирост: Δбег = х2 – х1 = 14,8-15,2 = -0,4 с Относительный прирост: 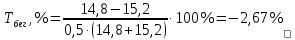 Найдем темпы роста результатов в беге на 1000 м: Абсолютный прирост: ΔКуп = х2 – х1 = 246-253 = -7 м Относительный прирост: 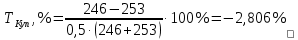 Найдем абсолютные и относительные приросты средних результатов спортсменов экспериментальной группы. Прыжок в высоту с места. Абсолютный прирост: Δпр = х2 – х1 = 50,3-44,5= 5,8см Относительный прирост: 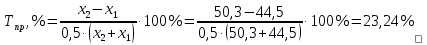 Бег на 100 м Абсолютный прирост: Δбег = х2 – х1 = 14,6-15,1 = -0,5 с Относительный прирост: 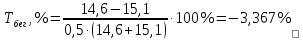 Бег на 1000 м Абсолютный прирост: ΔКуп = х2 – х1 = 245-250 = -5м Относительный прирост: 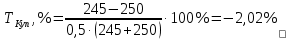
Построим график темпов прироста показателей у спортсменов контрольной и экспериментальной групп 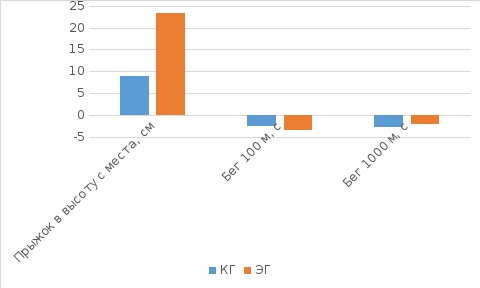 Рис. 1. Относительный прирост результатов тестирования спортсменов контрольной и экспериментальной групп (%). 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
