Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное
Образовательное учреждение высшего образования
«Комсомольский-на-Амуре государственный университет»
Электротехнический факультет
Кафедра «Промышленная электроника»

Расчетно-графическая работа
по дисциплине «Методы цифровой обработки сигналов»
Вариант №07
Студент группы 0ПЭм-1 Н.С. Межецкий
Преподаватель С.Г. Марущенко
2021
 Содержание Содержание
Задание №1 3
Задание №2 9
Задание №3 14
Задание №4 18
Список использованных источников 22
 Задание №1 Задание №1
Непрерывное сообщение передается от источника к получателю по дискретному каналу связи. Требуется:
1. Изобразить обобщённую структурную схему системы связи для передачи непрерывных сообщений дискретными сигналами, привести подробное описание назначения входящих в нее блоков. Преобразование сообщения и сигналов в системе связи проиллюстрировать качественным приведением временных и спектральных диаграмм для следующих точек тракта:
на выходе источника непрерывного сообщения (сигнала);
на выходе преобразователя аналог-цифра;
дискретизированной последовательности (АИМ сигнала);
на выходе АЦП (только временную диаграмму).
2. Найти величину шага квантования  и дисперсию шума квантования и дисперсию шума квантования 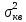
Исходные данные согласно варианту:
1. 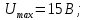
2. 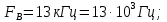
3. 
4.
Решение:
На рисунке 1 изображена обобщенная структурная схема системы связи для передачи непрерывного сообщения дискретными сигналами.

Рисунок 1 – Обобщенная структурная схема системы связи для передачи непрерывного сообщения дискретными сигналами.
 Непрерывный аналоговый сигнал от источника соединения S(t) поступает на вход аналогового фильтра нижних частот (НЧ), где спектр сигнала ограничивается частотой среза ФНЧ. Частота среза ФНЧ настроена на значение Fв. Аналоговый сигнал Sa(t) с выхода аналогового фильтра НЧ поступает на вход аналого-цифрового преобразователя, состоящего из дискретизатора и квантователя. В дискретизаторе сигнал преобразуется в последовательность равноотстоящих импульсов X (nT), амплитуды которых пропорциональны значениям входного аналогового сигнала в моменты выборки. Таким образом, дискретизатор (или импульсный модулятор) преобразует исходный аналоговый сигнал Sa(t) в дискретную последовательность, или в модулированную импульсную последовательность (МИП). Интервал между импульсами выбирается в соответствии с теорией Котельникова: Непрерывный аналоговый сигнал от источника соединения S(t) поступает на вход аналогового фильтра нижних частот (НЧ), где спектр сигнала ограничивается частотой среза ФНЧ. Частота среза ФНЧ настроена на значение Fв. Аналоговый сигнал Sa(t) с выхода аналогового фильтра НЧ поступает на вход аналого-цифрового преобразователя, состоящего из дискретизатора и квантователя. В дискретизаторе сигнал преобразуется в последовательность равноотстоящих импульсов X (nT), амплитуды которых пропорциональны значениям входного аналогового сигнала в моменты выборки. Таким образом, дискретизатор (или импульсный модулятор) преобразует исходный аналоговый сигнал Sa(t) в дискретную последовательность, или в модулированную импульсную последовательность (МИП). Интервал между импульсами выбирается в соответствии с теорией Котельникова: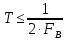 где Fв – верхняя граничная частота в спектре исходного аналогового сигнала Sa(t). где Fв – верхняя граничная частота в спектре исходного аналогового сигнала Sa(t).
Дискретизацию по времени можно осуществить с помощью импульсного модулятора. Импульсный модулятор представляет собой устройство с двумя входами, на один из которых подаётся исходный аналоговый сигнал Sa(t). На другой вход поступают короткие синхронизирующие импульсы с интервалом повторения Т. Модулятор построен таким образом, что в момент подачи каждого синхронизирующего импульса происходит изменение мгновенного значения сигнала Sa(t). На выходе модулятора возникает последовательность импульсов, каждый из которых имеет площадь, пропорциональную соответствующему отсчётному значению аналогового сигнала.
 Дискретный сигнал X (nT) квантуется по уровню и преобразуется в дискретную, квантованную по уровню последовательность Дискретный сигнал X (nT) квантуется по уровню и преобразуется в дискретную, квантованную по уровню последовательность 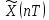 – цифровой сигнал. С выхода АЦП цифровой сигнал поступает на вход цифрового фильтра. В цифровом фильтре осуществляется цифровая обработка сигнала – цифровой сигнал. С выхода АЦП цифровой сигнал поступает на вход цифрового фильтра. В цифровом фильтре осуществляется цифровая обработка сигнала 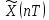 , представленного набором кодовых символов, соответствующих системе представления отсчётов в цифровом фильтре. Обычно числа в цифровом фильтре представляются в двоичной системе счисления с плавающей запятой и меньших 1, чтобы при выполнении операций в ЦФ не происходило переполнений. , представленного набором кодовых символов, соответствующих системе представления отсчётов в цифровом фильтре. Обычно числа в цифровом фильтре представляются в двоичной системе счисления с плавающей запятой и меньших 1, чтобы при выполнении операций в ЦФ не происходило переполнений.
Тактовая частота цифрового фильтра кратна частоте дискретизации по времени 1 T . Сигнал 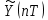 , обработанный в ЦФ по заданному алгоритму, с выхода ЦФ поступает в линию связи, обеспечивающую передачу сигналов от источника к приёмнику. Сигналы на выходе линии связи могут отличаться от переданных, вследствие затухания, искажения или воздействия помех. Помехами называют любые мешающие возмущения. Однако, устанавливаемое для линии связи отношение сигнал/шум позволяет надёжно выделить логические уровни, т.е. обеспечивать верность передачи сообщений, закодированных в цифровом виде. На обобщённой структурной схеме не показано (т.к. в задании это не отражено), но предполагается, что перед линией связи и после линии связи стоят согласующие элементы, которые согласуют волновое сопротивление связи с остальными частями схемы. Из линии связи сигнал поступает на цифро-аналоговый преобразователь (ЦАП), где преобразуется в последовательность ступенек ya(t), амлитуды которых пропорциональны соответствующим значениям цифрового сигнала , обработанный в ЦФ по заданному алгоритму, с выхода ЦФ поступает в линию связи, обеспечивающую передачу сигналов от источника к приёмнику. Сигналы на выходе линии связи могут отличаться от переданных, вследствие затухания, искажения или воздействия помех. Помехами называют любые мешающие возмущения. Однако, устанавливаемое для линии связи отношение сигнал/шум позволяет надёжно выделить логические уровни, т.е. обеспечивать верность передачи сообщений, закодированных в цифровом виде. На обобщённой структурной схеме не показано (т.к. в задании это не отражено), но предполагается, что перед линией связи и после линии связи стоят согласующие элементы, которые согласуют волновое сопротивление связи с остальными частями схемы. Из линии связи сигнал поступает на цифро-аналоговый преобразователь (ЦАП), где преобразуется в последовательность ступенек ya(t), амлитуды которых пропорциональны соответствующим значениям цифрового сигнала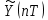 . Ступенчатое напряжение ya(t) слаживается аналоговым фильтром НЧ, на выходе которого восстанавливается аналоговый сигнал S′(t). Обычно, для уменьшения искажений в восстанавливающем фильтре, в качестве последнего выбирают фильтры Баттерворта с порядком n>5 . Ступенчатое напряжение ya(t) слаживается аналоговым фильтром НЧ, на выходе которого восстанавливается аналоговый сигнал S′(t). Обычно, для уменьшения искажений в восстанавливающем фильтре, в качестве последнего выбирают фильтры Баттерворта с порядком n>5
 Преобразование сигналов в системе связи проиллюстрировано качественными временными и спектральными диаграммами (рисунок 2). Временная диаграмма непрерывного аналогового сигнала на выходе источника непрерывного сообщения приведена на рисунке 2 (а). Спектральная диаграмма данного сигнала имеет вид, показанный на рисунке 2 (б). После прохождения сигнала через фильтр низких частот (ФНЧ), его спектр сужается и ограничивается верхней граничной частотой ωв = 2πFв (рисунок 2(г)). Из временной функции данного сигнала устраняются выбросы, сформированные высокочастотными составляющими, которые были вырезаны из спектра фильтром НЧ. Временная диаграмма отфильтрованного и ограниченного по частоте сигнала показана на рисунке 2 (в). Временная диаграмма модулированной импульсной последовательности (дискретного сигнала) X (nT) приведена на рисунке 2 (д). Выборки сигнала осуществляются с периодом T, определённым по теореме Котельникова. Известно, что если исходный аналоговый сигнал, имеющий спектральную плотность Sa (ω), был подвергнут дискретизации, то спектральная плотность дискретного сигнала будет определяться как: Преобразование сигналов в системе связи проиллюстрировано качественными временными и спектральными диаграммами (рисунок 2). Временная диаграмма непрерывного аналогового сигнала на выходе источника непрерывного сообщения приведена на рисунке 2 (а). Спектральная диаграмма данного сигнала имеет вид, показанный на рисунке 2 (б). После прохождения сигнала через фильтр низких частот (ФНЧ), его спектр сужается и ограничивается верхней граничной частотой ωв = 2πFв (рисунок 2(г)). Из временной функции данного сигнала устраняются выбросы, сформированные высокочастотными составляющими, которые были вырезаны из спектра фильтром НЧ. Временная диаграмма отфильтрованного и ограниченного по частоте сигнала показана на рисунке 2 (в). Временная диаграмма модулированной импульсной последовательности (дискретного сигнала) X (nT) приведена на рисунке 2 (д). Выборки сигнала осуществляются с периодом T, определённым по теореме Котельникова. Известно, что если исходный аналоговый сигнал, имеющий спектральную плотность Sa (ω), был подвергнут дискретизации, то спектральная плотность дискретного сигнала будет определяться как:

где Δ = T – шаг дискретизации
Итак, спектр сигнала, полученного в результате идеальной дискретизации бесконечно короткими стробирующими импульсами, представляет собой сумму бесконечного числа "копий" спектра исходного аналогового сигнала. Копии располагаются на оси частот через одинаковые интервалы 2πT, равные значению угловой частоты первой гармоники дискретизирующей импульсной последовательности. График спектральной плотности дискретного сигнала X (nT) показан на рисунке 2 (е). Временная диаграмма сигнала на выходе АЦП (рисунке 2 (ж)) представляет собой последовательность квантованных отсчётов исходного аналогового сигнала, представленных в двоичной системе счисления в соответствии с разрядностью АЦП.
 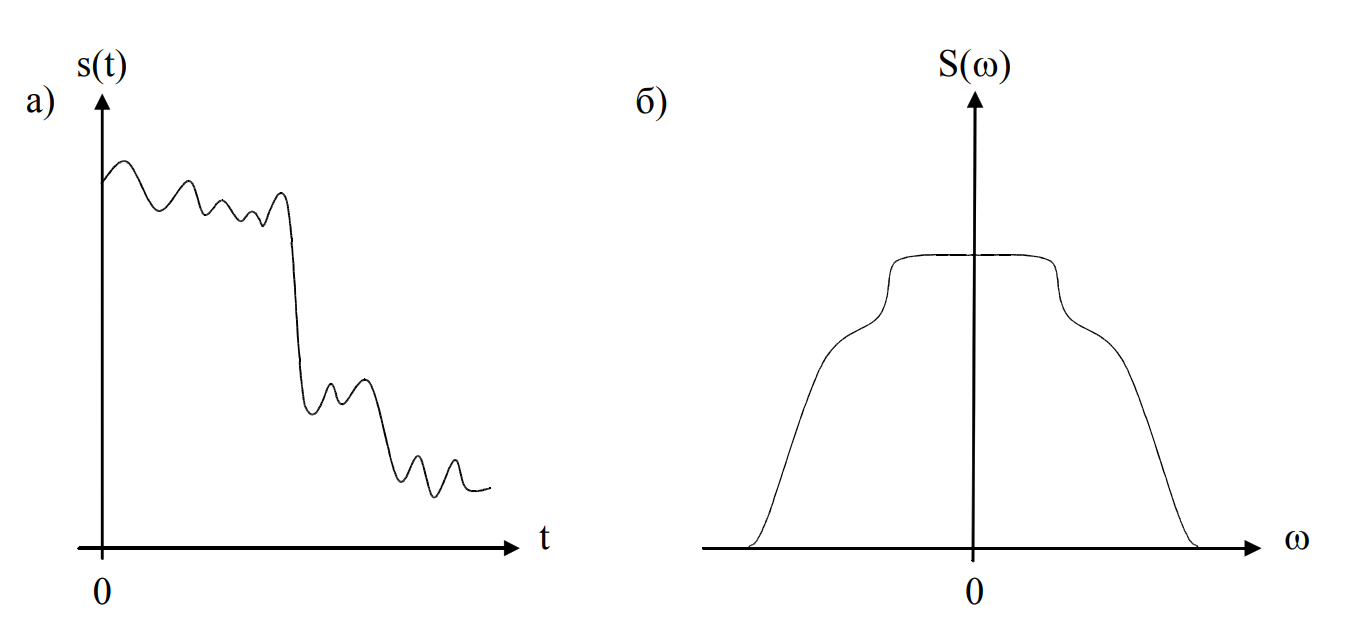
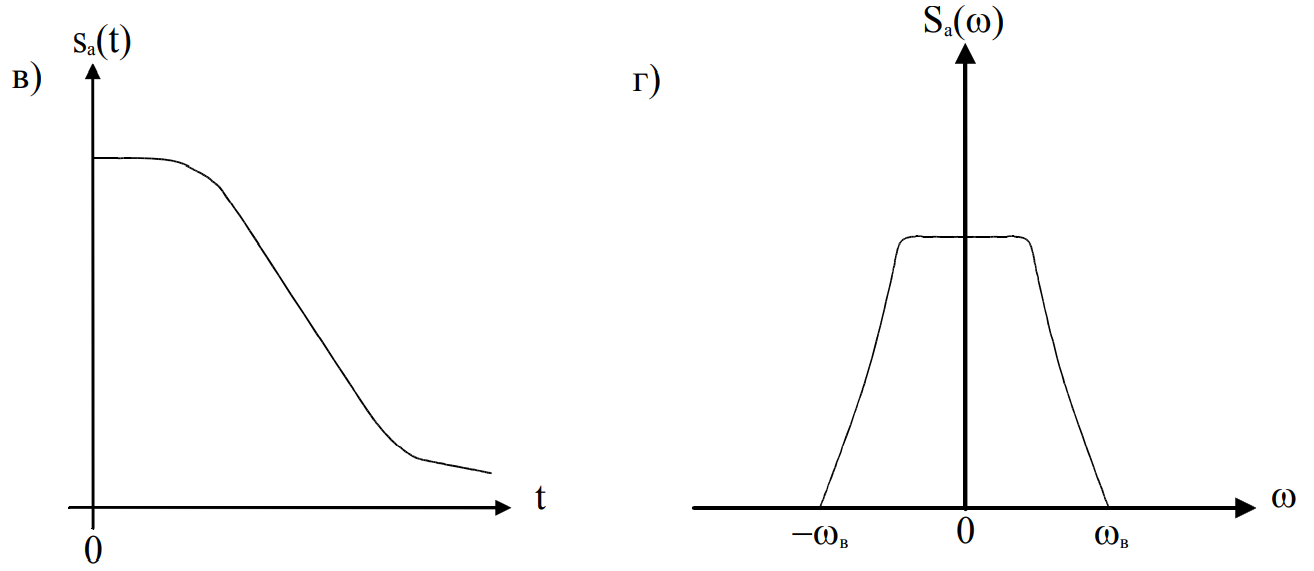

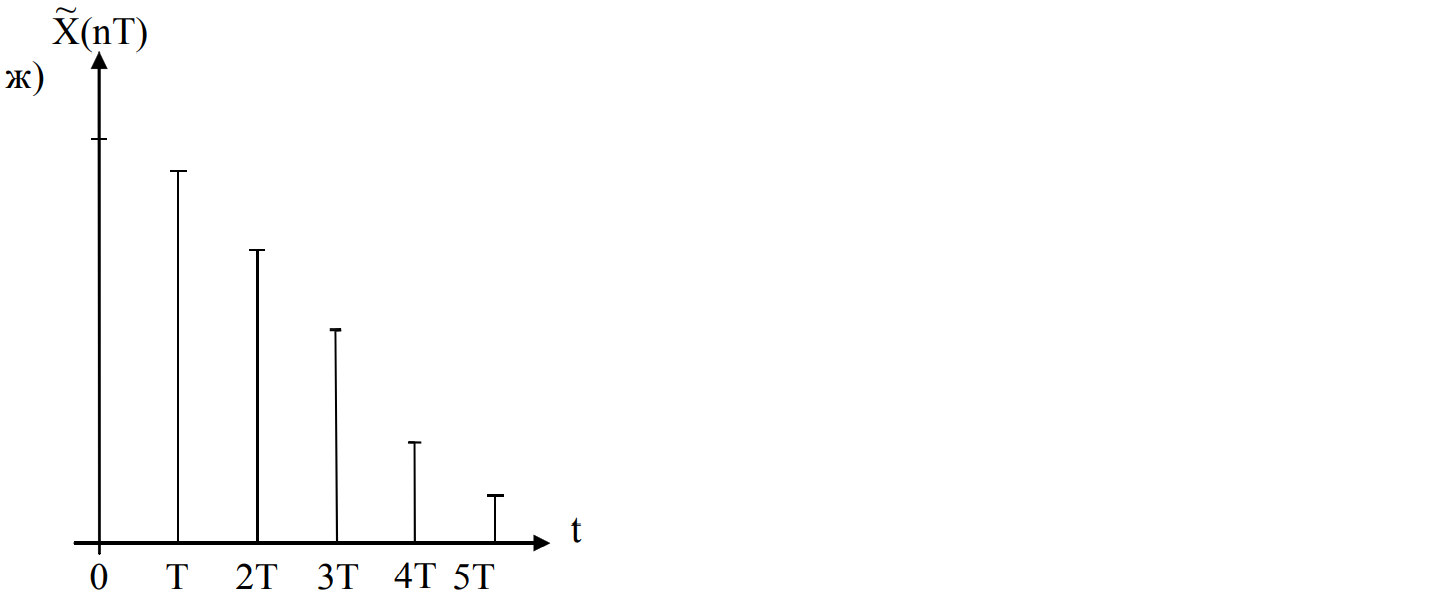
Рисунок 2 – Временные и спектральные диаграммы в различных точках тракта
 Найдем величину шага квантования по уровню: Найдем величину шага квантования по уровню:

Дисперсия шума квантования:
а) при округлении и усечении дополнительного кода

б) при усечении прямого и обратного кодов

 Задание №2 Задание №2
В предположении, что сигнал сообщения имеет гармоническую форму частотой Fв, требуется:
1. Изобразить временные диаграммы исходного сигнала (2,3 периода) и дискретизированной последовательности для него при условии, что дискретизация отсчётами производится с интервалом, в k раз меньшим по сравнению с шагом дискретизации, определяемым теоремой Котельникова.
2) Изобразить спектральные диаграммы исходного сигнала и дискретизированной последовательности.
3) Описать вид графиков временных и спектральных диаграмм на основе соответствующих теоретических положений.
Исходные данные:
1. 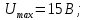
2. 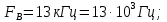
3. 
4.
Решение:
Запишем математическую модель для сигнала сообщения гармонической формы с частотой  : :

Период сигнала:
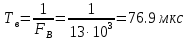
Шаг дискретизации, определяемый теоремой Котельникова:
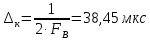
Шаг дискретизации, определяемый по условию задачи:

Приведем временные диаграммы исходного сигнала  и дискретизированной последовательности и дискретизированной последовательности  . В соответствии с условиями задачи, при дискретизации у нас получится 8 отсчетов за период. На рисунке 3 (а) изображена временная диаграмма исходного сигнала, на рисунке 3 (б) изображена дискретизированная последовательность данного сигнала. . В соответствии с условиями задачи, при дискретизации у нас получится 8 отсчетов за период. На рисунке 3 (а) изображена временная диаграмма исходного сигнала, на рисунке 3 (б) изображена дискретизированная последовательность данного сигнала.


    


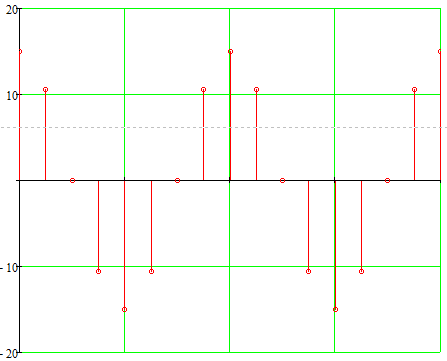
Рисунок 3 – Временные диаграммы исходного сигнала (а) и дискретизированной последовательности (б)
 Определим спектральные диаграммы исходного аналогового сигнала и дискретизированной последовательности. Для того, чтобы определить спектральную плотность гармонического колебания воспользуемся формулой Эйлера: Определим спектральные диаграммы исходного аналогового сигнала и дискретизированной последовательности. Для того, чтобы определить спектральную плотность гармонического колебания воспользуемся формулой Эйлера:

Для нахождения спектральной плотности данного сигнала воспользуемся обобщенной формулой Релея и свойством линейности преобразования Фурье. Сначала определим спектральную плотность комплексного экспоненциального сигнала:

Воспользовавшись обобщенной формулой Релея, имеем:
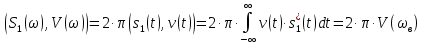
Следовательно, на основании фильтрующего свойства дельта функции имеем:
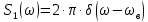
Воспользовавшись линейностью преобразования Фурье определим спектральную плотность гармонического колебания:
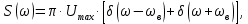
где 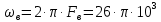 рад/с рад/с
Плотность дискретизированного сигнала есть бесконечная сумма копий спектра исходного аналогового сигнала. Копии располагаются на оси частот через равные промежутки  соответствующие первой гармонике частоты дискретизации: соответствующие первой гармонике частоты дискретизации:
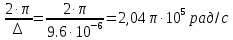
 Временная диаграмма исходного аналогового сигнала Временная диаграмма исходного аналогового сигнала  рисунок 3(а) представляет собой гармоническую функцию с амплитудой 15 В и периодом 76,9 мкс. Сигнал описывается непрерывной функцией, причем аргумент и значения функции могут принимать любые значения из заданных областей определения и допустимых значений. рисунок 3(а) представляет собой гармоническую функцию с амплитудой 15 В и периодом 76,9 мкс. Сигнал описывается непрерывной функцией, причем аргумент и значения функции могут принимать любые значения из заданных областей определения и допустимых значений.
Дискретизированный сигнал описывается временным рядом X(nT), значения которого представляют собой отсчеты исходного аналогового сигнала в строго фиксированные моменты времени. Область допустимых значений дискретной функции располагается в интервале  , в то время как аргумент функции может принимать лишь фиксированные значения , в то время как аргумент функции может принимать лишь фиксированные значения  , где n=0,1,2,3…, T= , где n=0,1,2,3…, T= - интервал дискретизации. - интервал дискретизации.

На одном периоде повторения исходного сигнала получается 5 отсчетов дискретного сигнала.
Спектральная диаграмма исходного аналогового сигнала приведена на рисунке 4 (а). Спектр гармонического сигнала симметричен относительно вертикальной оси, т.к. косинус функция четная. Спектр косинусоиды представляет собой сумму двух дельта-функций с площадью  каждая, расположенных на частотах каждая, расположенных на частотах 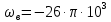 рад/с и рад/с и  рад/с соответственно. рад/с соответственно.
Спектральная диаграмма дискретизированной последовательности, как уже отмечалось выше, представляет собой копии спектральной диграммы исходного аналогового сигнала. Эти копии периодически повторяются, период повторения равен
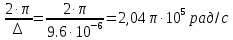

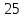


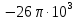
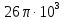


 , рад/с , рад/с
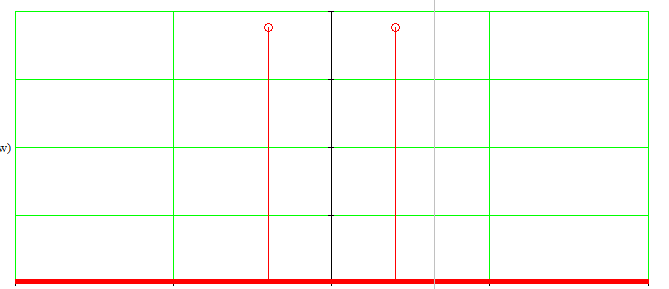
 

            
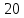



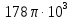

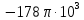


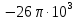
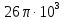
 , рад/с , рад/с
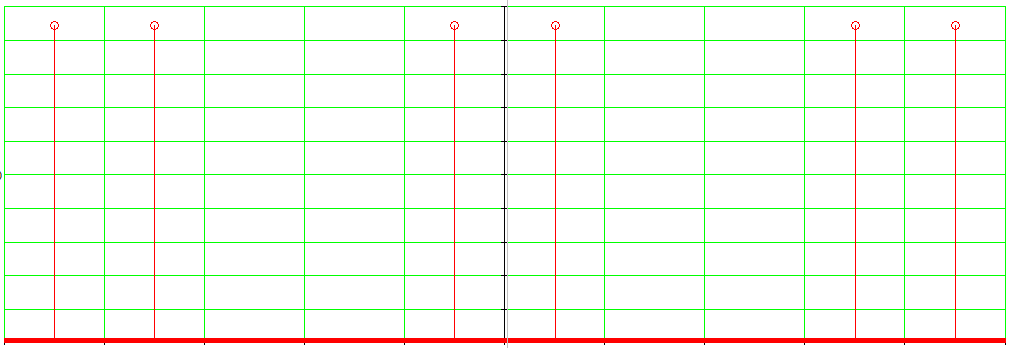
Рисунок 4 – Спектральные диаграммы аналогового (а) и дискретизитрованного (б) гармонического колебания
 Задание №3 Задание №3
В соответствии с дискретным преобразованием Фурье рассчитать и построить спектр сигнала на выходе АЦП (отсчеты после дискретизации представлены n- разрядными двоичными числами).
Исходные данные:
1. 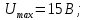
2. 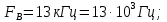
3. 
4.
Решение:
Используя дискретное преобразование Фурье, рассчитаем и построим спектр сигнала на выходе АЦП. Отсчеты дискретного сигнала на выходе АЦП представляют собой 10-ти разрядный двоичный код числа 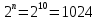 , которые в зависимости от схемы включения АЦП, могут быть записаны либо в прямом, либо в дополнительном коде, либо в двоичном смещенном коде. Так как исходный код аналогового сигнала изменяется от , которые в зависимости от схемы включения АЦП, могут быть записаны либо в прямом, либо в дополнительном коде, либо в двоичном смещенном коде. Так как исходный код аналогового сигнала изменяется от  до до 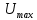 , то двоичные числа на выходе АЦП удобнее представлять в дополнительном коде, тогда диапазон 10-разрядных двоичных чисел в дополнительном коде составит от -512 до 511. Оцифрованный сигнал будет описываться следующей зависимостью: , то двоичные числа на выходе АЦП удобнее представлять в дополнительном коде, тогда диапазон 10-разрядных двоичных чисел в дополнительном коде составит от -512 до 511. Оцифрованный сигнал будет описываться следующей зависимостью:
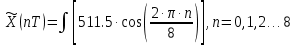
В соответствии с данной формулой на интервале периодичности дискретного сигнала имеем следующие десятичные эквиваленты двоичных отсчетов на выходе АЦП (таблица 1)
Таблица 1 – Десятичные эквиваленты двоичных чисел
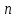
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
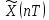
|
512
|
362
|
0
|
-362
|
-512
|
-362
|
0
|
362
|
 Паре преобразований Фурье для аналоговых сигналов соответствует их дискретный аналог называемый как дискретное преобразование Фурье (ДПФ) и обратное дискретное преобразование Фурье (ОДПФ), которые описываются следующими выражениями: Паре преобразований Фурье для аналоговых сигналов соответствует их дискретный аналог называемый как дискретное преобразование Фурье (ДПФ) и обратное дискретное преобразование Фурье (ОДПФ), которые описываются следующими выражениями:
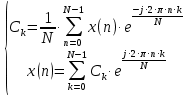
Определим коэффициенты ДПФ 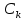 , полагая что , полагая что  . Для определения коэффициента . Для определения коэффициента  воспользуемся свойством ДПФ: воспользуемся свойством ДПФ:
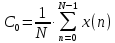
В нашем случае 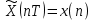 . .

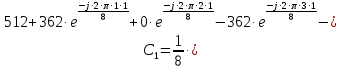

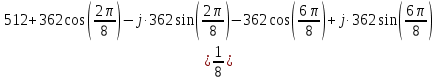
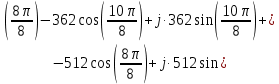
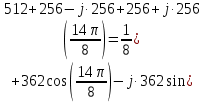
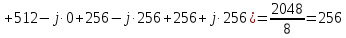
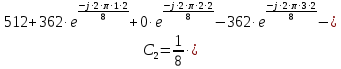
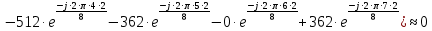
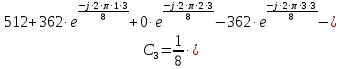

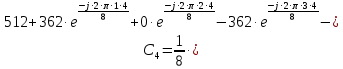


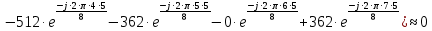
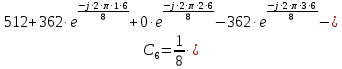

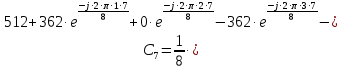
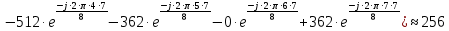
 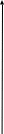 
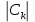
После определения всех коэффициентов построим спектральную диаграмму сигнала на выходе АЦП смотри рисунок 5
         
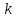
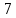
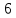

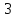

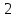


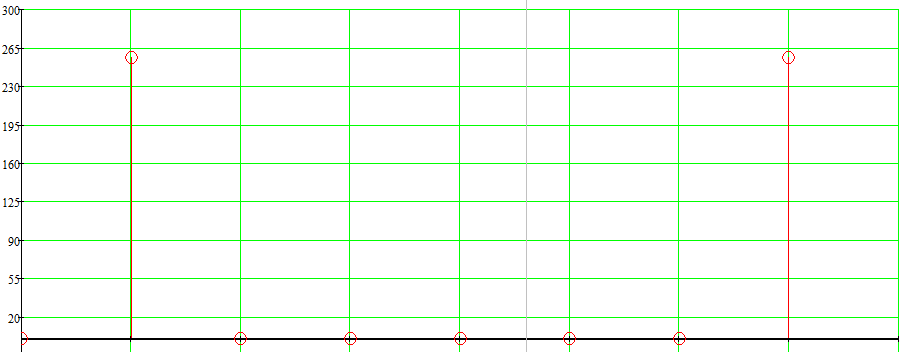
Рисунок 5 – Спектральная диаграмма сигнала на выходе АЦП.
Небольшое отличие коэффициентов от целых чисел связано с шумом квантования по уровню исходного гармонического сигнала и с несиммитрией разрядной сетки АЦП при представлении отрицательных и положительных чисел в двоичном дополнительном коде.
 Задание №4 Задание №4
На стороне передачи осуществляется предварительная цифровая обработка сигнала, поступающего с выхода АЦП, в соответствии с алгоритмом вида:
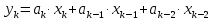
Где весовые коэффициенты  . .
Требуется:
Изобразить структурную схему цифрового фильтра (ЦФ) и описать принцип его работы.
Определить импульсную характеристику данного ЦФ.
Определить системную функцию ЦФ.
Определить частотный коэффициент передачи ЦФ.
Рассчитать сигнал на выходе цифрового фильтра для отсчета одного периода входного сигнала и показать его временную диаграмму.
Решение:
Подставив значения коэффициентов варианта задания имеем:
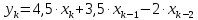
Структурная схема цифрового фильтра, реализующего данный алгоритм фильтрации приведена на рисунке 6.

Рисунок 6 – Структурная схема цифрового фильтра
 Данный фильтр является нерекурсивным (трансверсальным) фильтром второго порядка. Нерекурсивный фильтр проводит взвешенное суммирование предшествующих отсчетов входного сигнала и не использует прошлые отсчеты выходного сигнала. Данный фильтр является нерекурсивным (трансверсальным) фильтром второго порядка. Нерекурсивный фильтр проводит взвешенное суммирование предшествующих отсчетов входного сигнала и не использует прошлые отсчеты выходного сигнала.
По определению импульсная характеристика представляет собой дискретный сигнал 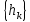 , который является реакцией ЦЫ на «единичный импульс» (1, 0, 0, 0 …). , который является реакцией ЦЫ на «единичный импульс» (1, 0, 0, 0 …).

В момент каждого отсчета ЦФ проводит операцию взвешенного суммирования всех предыдущих значений входного сигнала, причем роль последовательности весовых коэффициентов играют отсчеты импульсной характеристики. Тогда для нашего варианта задания импульсная характеристика будет иметь вид:
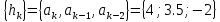
Вид импульсной характеристики представлен на рисунке 7:
 

 
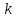
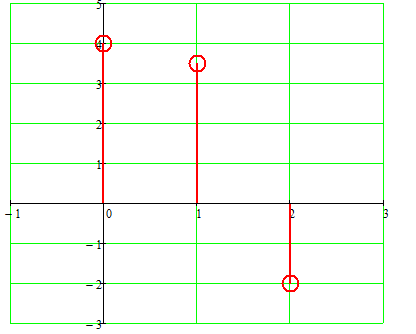
Рисунок 7 – Импульсная характеристика цифрового фильтра
Системной функцией ЦФ называют отношение z-преобразования выходного сигнала к z-преобразованию сигнала на входе. Применив z-преобразования к обеим частям выражения получим:
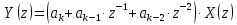
 Тогда системная функция ЦФ определится как: Тогда системная функция ЦФ определится как:
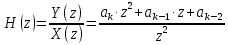
С учетом коэффициентов варианта задания имеем:
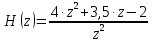
Для того чтобы определить частотный коэффициент передачи ЦФ проведем замену переменой  , где , где 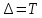 – шаг дискретизации. – шаг дискретизации.

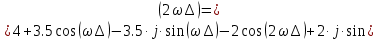

Найдем значение частотного коэффициента передачи, при 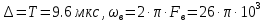 рад/с. рад/с.


Модуль частотного коэффициента передачи на заданной частоте будет равен:

Так как исходный дискретный сигнала является периодическим, то последовательность отсчетов на входе ЦФ будет иметь следующий вид:
512, 362, 0, -362, -512, -362, 0, 362…
Рассчитаем сигнал на выходе ЦФ для одного периода входного сигнала. Будем считать. Что фильтр работает в установившемся режиме, т.е предшествующие отсчеты входного сигнала существует Результаты расчетов сведем в таблицу 2.
 Таблица 2 – результаты расчетов по алгоритму цифровой фильтрации Таблица 2 – результаты расчетов по алгоритму цифровой фильтрации
k
|
-2
|
-1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
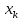
|
0
|
362
|
512
|
362
|
0
|
-362
|
-512
|
-362
|
0
|
362
|

|
x
|
x
|
3315
|
2172
|
-243
|
-1240
|
-3315
|
-2172
|
243
|
2516
|
 

Построим временную диаграмму одного периода на выходе ЦФ смотри рисунок 8.
 
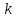
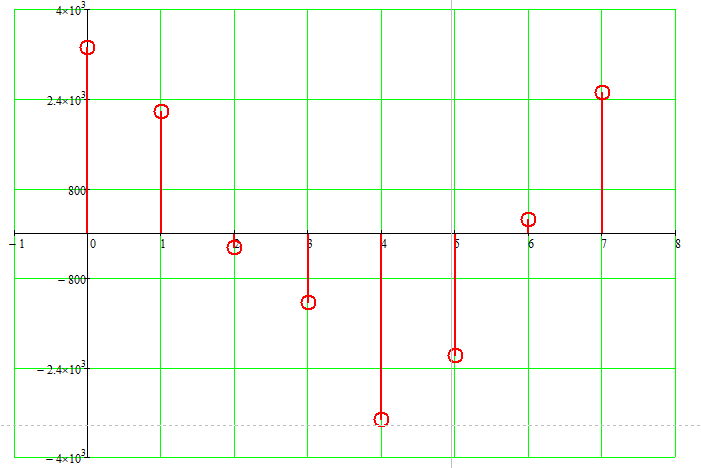
Рисунок 8 – Временная диаграмма на выходе ЦФ.
При обработке данного сигнала в ЦФ происходит заметное искажение выходного сигнала. Также ЦФ осуществляет значительное усиление по амплитуде и сдвиг по фазе.
Марущенко С. Г. Основы цифровой обработки сигналов: Учеб.пособ-ие. – Комсомольск-на-Амуре: ГОУВПО «КнАГТУ», 2006 – 196 с.
|
 Скачать 437.17 Kb.
Скачать 437.17 Kb.
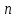
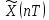
 Паре преобразований Фурье для аналоговых сигналов соответствует их дискретный аналог называемый как дискретное преобразование Фурье (ДПФ) и обратное дискретное преобразование Фурье (ОДПФ), которые описываются следующими выражениями:
Паре преобразований Фурье для аналоговых сигналов соответствует их дискретный аналог называемый как дискретное преобразование Фурье (ДПФ) и обратное дискретное преобразование Фурье (ОДПФ), которые описываются следующими выражениями: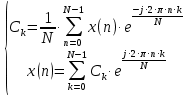
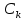 , полагая что
, полагая что  . Для определения коэффициента
. Для определения коэффициента  воспользуемся свойством ДПФ:
воспользуемся свойством ДПФ: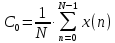
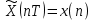 .
.
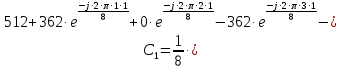

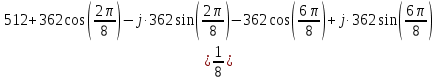
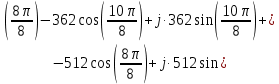
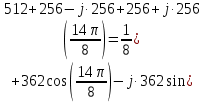
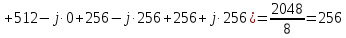
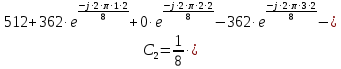
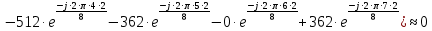
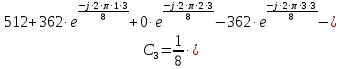

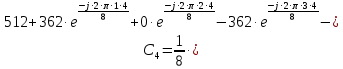


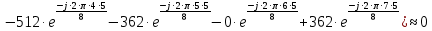
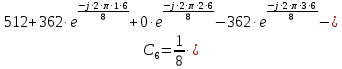

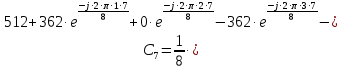
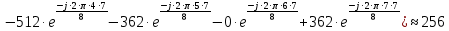


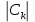










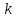
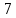
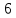

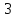

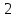



 Задание №4
Задание №4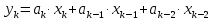
 .
.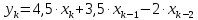

 Данный фильтр является нерекурсивным (трансверсальным) фильтром второго порядка. Нерекурсивный фильтр проводит взвешенное суммирование предшествующих отсчетов входного сигнала и не использует прошлые отсчеты выходного сигнала.
Данный фильтр является нерекурсивным (трансверсальным) фильтром второго порядка. Нерекурсивный фильтр проводит взвешенное суммирование предшествующих отсчетов входного сигнала и не использует прошлые отсчеты выходного сигнала.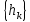 , который является реакцией ЦЫ на «единичный импульс» (1, 0, 0, 0 …).
, который является реакцией ЦЫ на «единичный импульс» (1, 0, 0, 0 …).
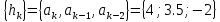





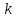

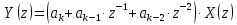
 Тогда системная функция ЦФ определится как:
Тогда системная функция ЦФ определится как: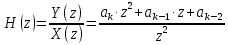
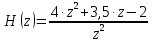
 , где
, где 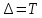 – шаг дискретизации.
– шаг дискретизации.
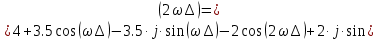

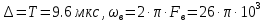 рад/с.
рад/с.


 Таблица 2 – результаты расчетов по алгоритму цифровой фильтрации
Таблица 2 – результаты расчетов по алгоритму цифровой фильтрации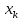






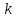

 Список использованных источников
Список использованных источников
 и дисперсию шума квантования
и дисперсию шума квантования 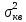
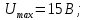
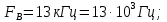



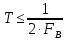 где Fв – верхняя граничная частота в спектре исходного аналогового сигнала Sa(t).
где Fв – верхняя граничная частота в спектре исходного аналогового сигнала Sa(t).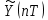 , обработанный в ЦФ по заданному алгоритму, с выхода ЦФ поступает в линию связи, обеспечивающую передачу сигналов от источника к приёмнику. Сигналы на выходе линии связи могут отличаться от переданных, вследствие затухания, искажения или воздействия помех. Помехами называют любые мешающие возмущения. Однако, устанавливаемое для линии связи отношение сигнал/шум позволяет надёжно выделить логические уровни, т.е.
, обработанный в ЦФ по заданному алгоритму, с выхода ЦФ поступает в линию связи, обеспечивающую передачу сигналов от источника к приёмнику. Сигналы на выходе линии связи могут отличаться от переданных, вследствие затухания, искажения или воздействия помех. Помехами называют любые мешающие возмущения. Однако, устанавливаемое для линии связи отношение сигнал/шум позволяет надёжно выделить логические уровни, т.е. 







 :
:
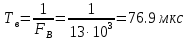
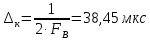

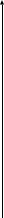

 и дискретизированной последовательности
и дискретизированной последовательности  . В соответствии с условиями задачи, при дискретизации у нас получится 8 отсчетов за период. На рисунке 3 (а) изображена временная диаграмма исходного сигнала, на рисунке 3 (б) изображена дискретизированная последовательность данного сигнала.
. В соответствии с условиями задачи, при дискретизации у нас получится 8 отсчетов за период. На рисунке 3 (а) изображена временная диаграмма исходного сигнала, на рисунке 3 (б) изображена дискретизированная последовательность данного сигнала. 

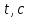







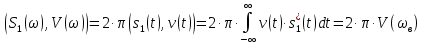
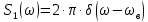
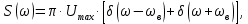
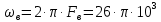 рад/с
рад/с соответствующие первой гармонике частоты дискретизации:
соответствующие первой гармонике частоты дискретизации: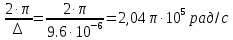
 , в то время как аргумент функции может принимать лишь фиксированные значения
, в то время как аргумент функции может принимать лишь фиксированные значения  , где n=0,1,2,3…, T=
, где n=0,1,2,3…, T= - интервал дискретизации.
- интервал дискретизации.
 каждая, расположенных на частотах
каждая, расположенных на частотах 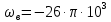 рад/с и
рад/с и  рад/с соответственно.
рад/с соответственно.

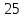

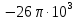
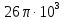


 , рад/с
, рад/с


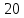



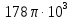

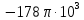


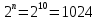 , которые в зависимости от схемы включения АЦП, могут быть записаны либо в прямом, либо в дополнительном коде, либо в двоичном смещенном коде. Так как исходный код аналогового сигнала изменяется от
, которые в зависимости от схемы включения АЦП, могут быть записаны либо в прямом, либо в дополнительном коде, либо в двоичном смещенном коде. Так как исходный код аналогового сигнала изменяется от  до
до 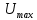 , то двоичные числа на выходе АЦП удобнее представлять в дополнительном коде, тогда диапазон 10-разрядных двоичных чисел в дополнительном коде составит от -512 до 511. Оцифрованный сигнал будет описываться следующей зависимостью:
, то двоичные числа на выходе АЦП удобнее представлять в дополнительном коде, тогда диапазон 10-разрядных двоичных чисел в дополнительном коде составит от -512 до 511. Оцифрованный сигнал будет описываться следующей зависимостью: