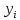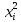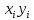Задача по метрологии. Решение. Находим среднее арифметическое значение по формуле 1
 Скачать 33.84 Kb. Скачать 33.84 Kb.
|
|
Вариант 8. Задача 1. При измерении активного сопротивления резистора были произведены десять равноточных измерений, результаты которых приведены в таблице. Оцените абсолютную и относительную погрешности и запишите результат измерения для доверительных вероятностей 0,95 и 0,99.
Решение. Находим среднее арифметическое значение по формуле:  
Вычисляем среднее квадратическое отклонение единичных результатов:   Предполагая, что погрешность распределена по нормальному закону, исключаем «промахи», т.е. измерения с грубыми погрешностями, для которых 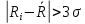 . .В этой задаче измерений, погрешность которых превышает  (0,511) нет. (0,511) нет.Вычисляем среднее квадратическое отклонение среднего арифметического (СКО результата измерений): 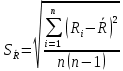 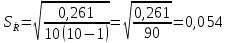 Определяем доверительные границы случайной погрешности при заданной доверительной вероятности: а) 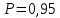 ; ;б) 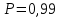 . . где 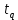 - коэффициент Стьюдента, зависящий от доверительной вероятности - коэффициент Стьюдента, зависящий от доверительной вероятности  и числа измерений и числа измерений  . Выбираем коэффициент . Выбираем коэффициент 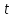 из таблицы. из таблицы.а) для  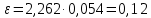 б) для 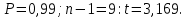 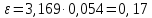 Окончательный результат записываем в форме: а) 953,7±0,1 Ом, 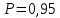 ; ;б) 953,7±0,2 Ом, 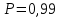 . .Задача 2. Оценить погрешность прямого однократного измерения напряжения  на сопротивлении на сопротивлении  , выполненного вольтметром класса точности , выполненного вольтметром класса точности  с верхним пределом измерения с верхним пределом измерения 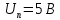 и имеющим сопротивление и имеющим сопротивление  . Известно, что дополнительные погрешности измерения из-за влияния магнитного поля и температуры не превышают соответственно . Известно, что дополнительные погрешности измерения из-за влияния магнитного поля и температуры не превышают соответственно  и и  допускаемой предельной погрешности. допускаемой предельной погрешности.Решение. Предел допускаемой относительной погрешности вольтметра на отметке 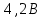 составляет: составляет:  (%) (%)При подсоединении вольтметра исходное напряжение 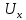 изменится из-за наличия внутреннего сопротивления вольтметра изменится из-за наличия внутреннего сопротивления вольтметра  и составит и составит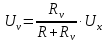 Тогда относительная методическая погрешность, обусловленная конечным значением  , будет равна , будет равна 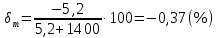 Данная методическая погрешность является систематической составляющей погрешности измерения и должна быть внесена в результат в виде поправки 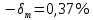 или в абсолютной форме или в абсолютной форме 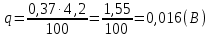 Тогда результат измерения с учетом поправки  Поскольку основная и дополнительная погрешности заданы своими граничными значениями, они могут рассматриваться как не исключенные систематические погрешности (НСП). При оценке границ НСП в соответствии с ГОСТ 8.207-76 их рассматривают как случайные величины, распределенные по равномерному закону. Тогда границы НСП результата измерения  можно вычислить по формуле: можно вычислить по формуле: где  - граница - граница 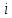 - той составляющей НСП, - той составляющей НСП, – коэффициент, определяемый принятой доверительной вероятностью – коэффициент, определяемый принятой доверительной вероятностью  . .Поскольку число суммируемых погрешностей меньше четырех, то коэффициент  определяем по графику зависимости определяем по графику зависимости  (с. 4 ГОСТ 8.207-76 ).  А в абсолютной форме 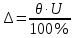  Ввиду того, что  ( ( , окончательный результат записывается в виде , окончательный результат записывается в виде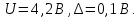 Задача 3. При проверке после ремонта вольтметра класса точности 1,5 с конечным значением шкалы 5 В, в точках шкалы 1, 2, 3, 4, 5 В получены показания образцового прибора, представленные в таблице. Определить, соответствует ли проверяемый вольтметр своему классу точности.
Решение. Предельная допускаемая абсолютная погрешность прибора равна 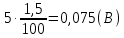 В каждой точке шкалы погрешность прибора не превышает предельно допустимую: 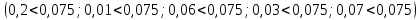 . . Следовательно, после ремонта прибор соответствует своему классу точности. Задача 4. Определить величину электрического тока 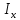 в общей цепи, а также значение абсолютной и относительной погрешности его определения, если токи, измеренные в ветвях цепи, равны в общей цепи, а также значение абсолютной и относительной погрешности его определения, если токи, измеренные в ветвях цепи, равны 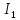 , ,  , ,  . .Классы точности амперметров, включенных в эти ветви, соответствуют  , ,  , ,  , а их предельные значения шкал , а их предельные значения шкал  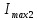 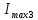
Решение. Величина тока в общей цепи  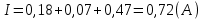 Погрешность измерения тока 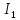 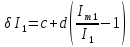 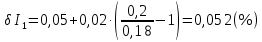 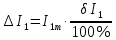 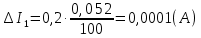 Погрешность измерения тока  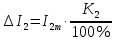  Погрешность измерения тока   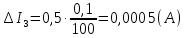 Предельная погрешность косвенного определения величины тока в общей цепи не превышает суммы абсолютных погрешностей измерений токов в отдельных ветвях цепи: 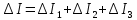 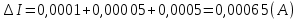 Относительная погрешность измерения:  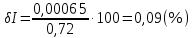 Таким образом,  Задача 5. Производится эксперимент по определению параметров транзисторов 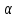 и и 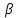 . Для этого измеряются микроамперметрами ток коллектора . Для этого измеряются микроамперметрами ток коллектора  и ток эмиттера и ток эмиттера  , а затем определяются параметры , а затем определяются параметры 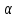 и и 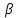 по формулам по формулам  , , 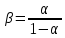 . Представьте результаты определения указанных параметров вместе с погрешностями их определения. Пределы измерения используемых микроамперметров, их классы точности ( . Представьте результаты определения указанных параметров вместе с погрешностями их определения. Пределы измерения используемых микроамперметров, их классы точности (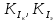 ) и полученные показания приведены в таблице. ) и полученные показания приведены в таблице.
Решение. Коэффициент передачи тока  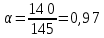 Погрешность косвенного определения 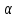 в этом случае находится как сумма относительных погрешностей измерений токов: в этом случае находится как сумма относительных погрешностей измерений токов:  (%) (%)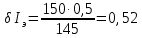 (%) (%) Абсолютная погрешность 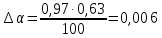 Таким образом,  Коэффициент усиления 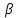 связан с связан с 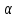 функциональной зависимостью функциональной зависимостью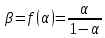 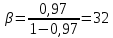 Погрешность определения β ∆β   Таким образом, погрешность определения β в этом случае велика. Задача 6. В информационно – измерительной системе для градуировки канала измерения нагрузки механического пресса, включающего тензометрический датчик и плату тензостанции на основе 16 –разрядного аналого – цифрового преобразователя, устанавливались усилия  , контролируемые эталонным динамометром и фиксировались числовые значения , контролируемые эталонным динамометром и фиксировались числовые значения 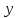 на выходе аналого – цифрового преобразователя. Диапазон градуировки 0…50 кН. Данные измерений на выходе аналого – цифрового преобразователя. Диапазон градуировки 0…50 кН. Данные измерений 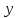 сведены в таблицу. Найти линейную функцию преобразования и построить градуировочную характеристику канала. Определить наибольшую относительную погрешность и приведенную погрешность канала измерения. сведены в таблицу. Найти линейную функцию преобразования и построить градуировочную характеристику канала. Определить наибольшую относительную погрешность и приведенную погрешность канала измерения.
Решение. Линейная функция преобразования  , представляющая собой зависимость между входной величиной , представляющая собой зависимость между входной величиной  и выходной величиной и выходной величиной 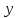 (значением на выходе аналого-цифрового преобразователя) находится методом наименьших квадратов. Для этой цели составим таблицу: (значением на выходе аналого-цифрового преобразователя) находится методом наименьших квадратов. Для этой цели составим таблицу:
Значения коэффициентов линейной зависимости находятся по формулам:  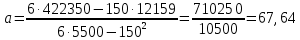 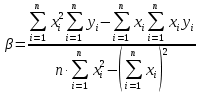  Функция преобразования измерительного канала имеет вид 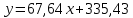 . Полученная зависимость может быть преобразована для вычисления неизвестной входной величины . Полученная зависимость может быть преобразована для вычисления неизвестной входной величины  . .Как видно из таблицы, наибольшая относительная погрешность 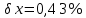 . Наибольшая абсолютная погрешность преобразования . Наибольшая абсолютная погрешность преобразования  наблюдается в точке наблюдается в точке 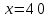 . Таким образом, приведенная погрешность равна . Таким образом, приведенная погрешность равна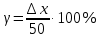  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


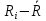
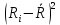
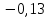
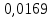
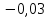
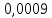



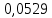
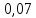
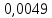

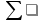


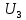


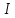 , Ампер
, Ампер
 , Ампер
, Ампер , мкА
, мкА