Задание 15. Решение Нахождение всех максимальных независимых множеств будем осуществлять последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (путем добавления к исследуемому множеству дополнительной,

• Название: Решение Нахождение всех максимальных независимых множеств будем осуществлять последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (путем добавления к исследуемому множеству дополнительной,
• Дата: 08.06.2022
• Размер: 334.5 Kb.
• Имя файла: Задание 15.doc
• Тип: Решение; #577425
• страница: 1 из 3

Задание № 15
1. В графе, представленном следующей матрицей смежности, найти все максимальные независимые множества.


Решение:

Нахождение всех максимальных независимых множеств будем осуществлять последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (путем добавления к исследуемому множеству дополнительной, не принадлежащей ему вершины и выяснением того, сохраняется ли независимость) и запоминанием максимальных множеств.

Для поиска максимально независимых множеств построим последовательность, где представляет совокупность независимых множеств:

;

;

;

;

;

;

;

;

;

.

Из последней совокупности множеств выбираем максимальные:



Ответ: .

2. Найти минимальную ДНФ для следующей слабоопределенной булевой функции.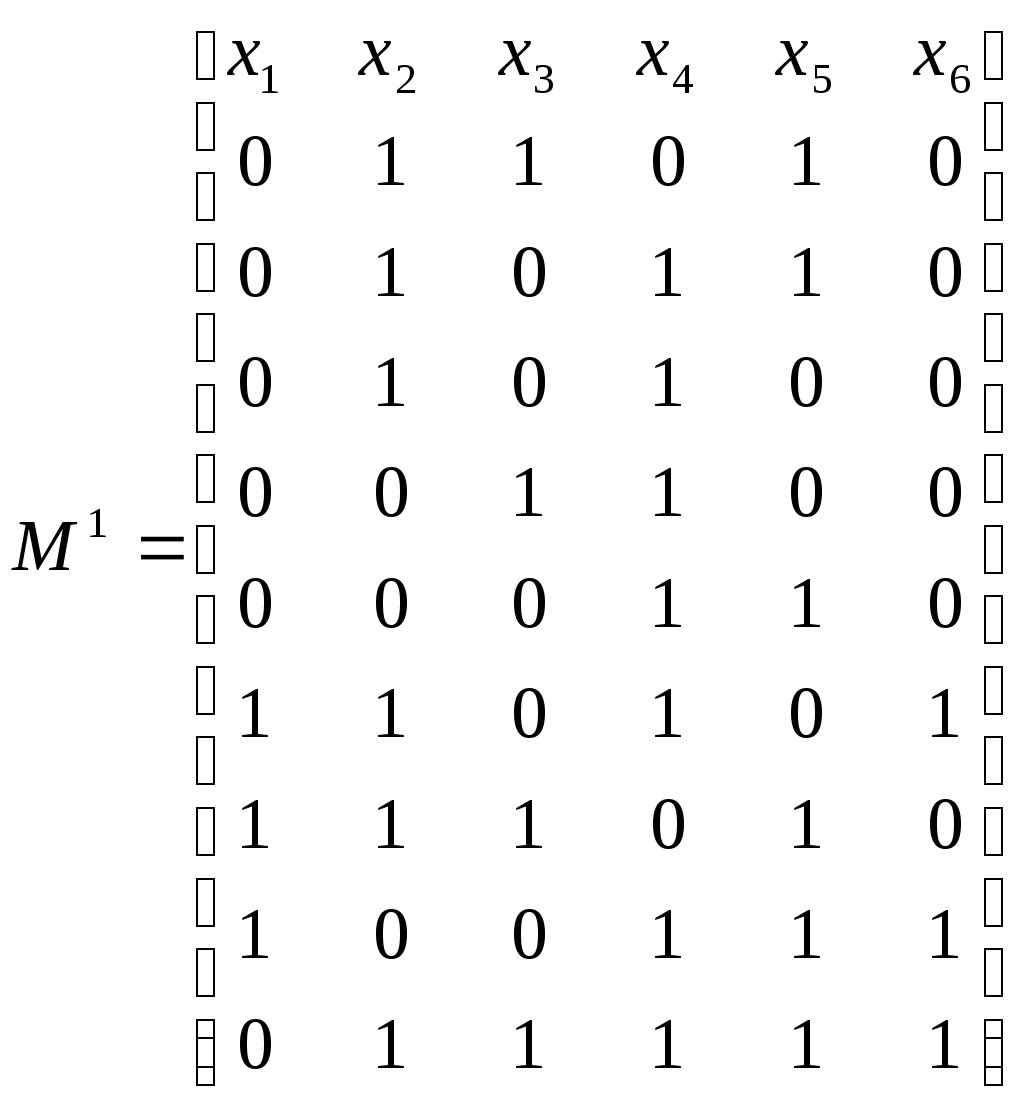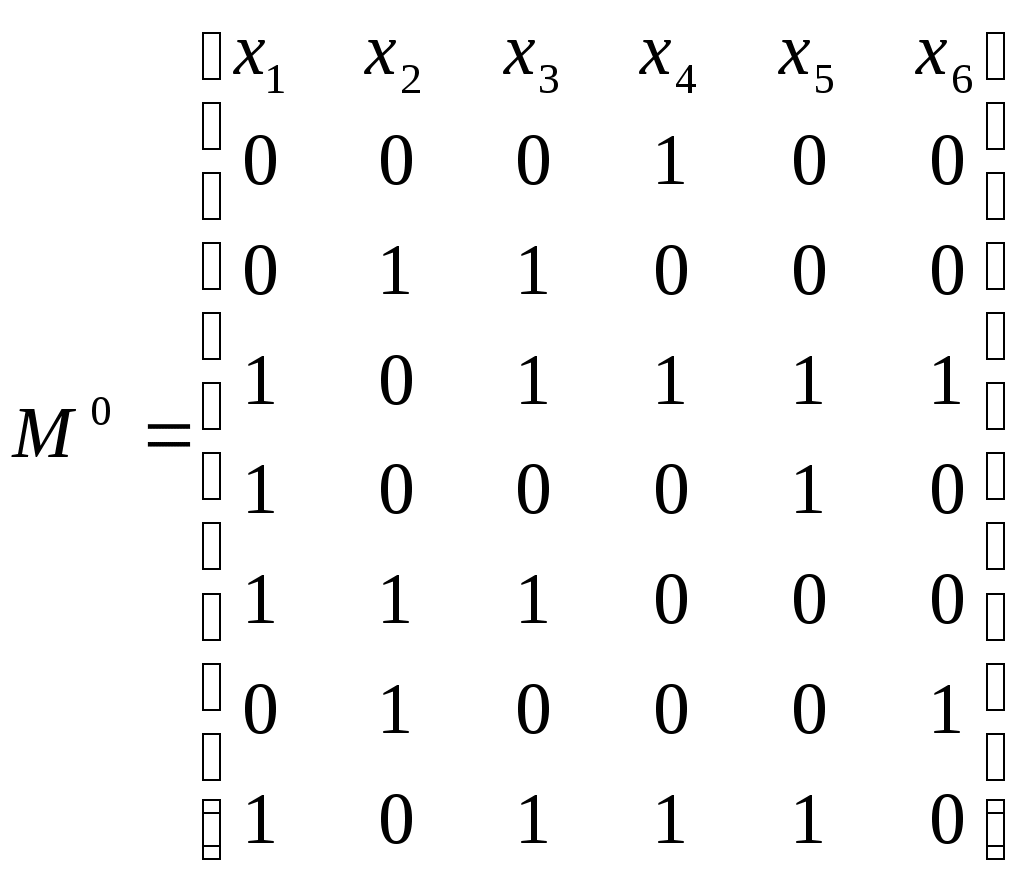

,
- область единичных значений,

- область нулевых значений.
Решение:

Дизъюнктивной нормальной формой (ДНФ) булевой функции называется дизъюнкция конечного числа элементарных конъюнкций. ДНФ записывается по таблице истинности.

Элементарной конъюнкцией называется логическое произведение любого конечного числа различных между собой булевых переменных, взятых со знаком инверсии или без него.

Сокращённая ДНФ – это ДНФ, состоящая из всех простых импликант заданной булевой функции.

Тупиковая ДНФ – это сокращенная ДНФ булевой функции, в которой отсутствуют лишние простые импликанты.

Минимальная ДНФ (МДНФ) – это тупиковая ДНФ с наименьшей суммой рангов конъюнкций по отношению ко всем другим тупиковым ДНФ, представляющим заданную булеву функцию. МДНФ может быть несколько.

Слабо определенной булевой функцией можно считать любую булеву функцию, не записанную в виде совершенной ДНФ.

Для нахождения минимальной ДНФ можно использовать различные методы. Для решения нашей задачи воспользуемся минимизацией с помощью карты Вейча.

1. 
   Для области построим карту Вейча и найдём сокращенную ДНФ.
   

								X4
						X5
					X6				X6
								1
		X3									1
	X2						1		1
								1			1
X1										1
		X3					1
									1

В таблице отразим полученную сокращённую ДНФ, состоящую из всех простых импликант заданной булевой функции на области :

x1	x2	x3	x4	x5	x6
0	0	1	-	-	-
-	1	-	-	1	-
-	1	-	1	-	-
-	0	0	1	1	-

Чтобы проверить найденное решение, построим импликантную таблицу на области :

						011010	010110	010100	001100	000110	110101	111010	100111	011111
0	0	1	-	-	-				+
-	1	-	-	1	-	+	+					+		+
-	1	-	1	-	-		+	+			+			+
-	0	0	1	1	-					+			+

Можно увидеть, что все простые импликанты являются обязательными для заданной булевой функции. Делаем вывод, что полученная сокращенная ДНФ является тупиковой и минимальной на области .

2. 
   Для области построим карту Вейча и найдём сокращенную КНФ.
   

								X4
						X5
					X6				X6
											0
		X3
	X2			0
					0
X1
		X3		0
								0	0
							0

В таблице отразим полученную сокращённую КНФ, состоящую из всех простых имплицент заданной булевой функции на области :

x1	x2	x3	x4	x5	x6
1	0	1	-	-	-
-	-	-	0	0	-
-	0	-	0	-	-
-	0	0	-	0	-

Чтобы проверить найденное решение, построим имплицентную таблицу на области :

						000100	011000	101111	100010	111000	010001	101110
1	0	1	-	-	-			+				+
-	-	-	0	0	-		+			+	+
-	0	-	0	-	-				+
-	0	0	-	0	-	+

Как видим, полученные простые импликанты на области , не пересекаются с простыми имплицентами на области .

3. Закодировать состояния методом «желательных соседств» и получить соответствующую минимальную систему ДНФ для автомата, представленного следующей таблицей переходов:

	00	01	10
1	-	3.0	5.0
2	1.1	4.0	-
3	3.0	-	2.-
4	2.1	3.-	4.1
5	4.0	2.1	3.1

Решение:

Суть метода «желательных соседств» заключается в том, что соседние состояния автомата кодируются наборами, различающимися состоянием только одного элемента памяти.

Система булевых функций в задании представляет сигналы возбуждения JK-триггеров.

JK-триггер – это асинхронный двухступенчатый триггер, он имеет два информационных входа. Таблица определяет переходы JK-триггера, согласно логической формулы .

Состояния JK-триггера:

	J K S
	00	01	10	11
0	0	0	1	1
1	1	0	1	0

Возможны следующие режимы работы JK-триггера:

J=0, K=0 – режим хранения информации (значение триггера не изменяется);

J=0, K=1 – режим сброса (триггер всегда устанавливается в 0);

J=1, K=0 – режим записи логической единицы (триггер устанавливается в 1);

J=1, K=1 – режим инверсии содержимого триггера.

Закодируем состояния автомата методом «желательных» соседств.

По виду представленной таблицы можно определить, что задан автомат Мили.

Таблица переходов:

	00	01	10
1	-	0	0
2	1	0	-
3	0	-	-
4	1	-	1
5	0	1	1

Таблица выходов:

	00	01	10
1	-	3	5
2	1	4	-
3	3	-	2
4	2	3	4
5	4	2	3