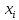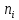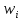теория. Теория вероятности. Решение. Найдем недостающее значение p P p1p2p3 1 p3Pp1p2 p310,10,50,4
 Скачать 85.67 Kb. Скачать 85.67 Kb.
|
ПОСТРОИТЬ график функции распределения ВЕРОЯТНОСТЕЙ для этой задачи. Решение. Найдем недостающее значение p P= 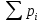 = p1+p2+p3 = 1 = p1+p2+p3 = 1p3=P-p1-p2 p3=1-0,1-0,5=0,4 Найдем математическое ожидание М(x)= 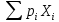 М(x)=2*0,1+4*0,5+8*0,4=0,2+2+3,2=5,4 Найдем математическое ожидание 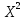 М( 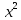 )= )=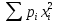 М( 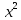 )= )=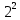 *0,1+ *0,1+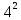 *0,5+ *0,5+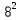 *0,4=4*0,1+16*0,5+64*0,4=0,4+8+25,6=34 *0,4=4*0,1+16*0,5+64*0,4=0,4+8+25,6=34Найдем дисперсию D= М( 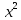 ) – ( ) – (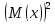 ) )D=34- 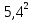 = 4,84 = 4,84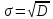 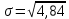 = 2,2 = 2,2Для построения графика найдем F(x) F(x)=P(X 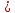 x) x)Пусть х 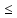 2, то F(x)=0 2, то F(x)=0Пусть 2 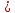 х х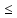 4, то F(x)= 0,1 4, то F(x)= 0,1Пусть 4 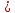 х х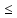 8, то F(x)= 0,1+0,5=0,6 8, то F(x)= 0,1+0,5=0,6Пусть x 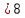 , то F(x)= 0,6+0,4=1 , то F(x)= 0,6+0,4=1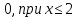 F(x) = 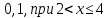 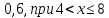 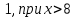 График функции распределения: 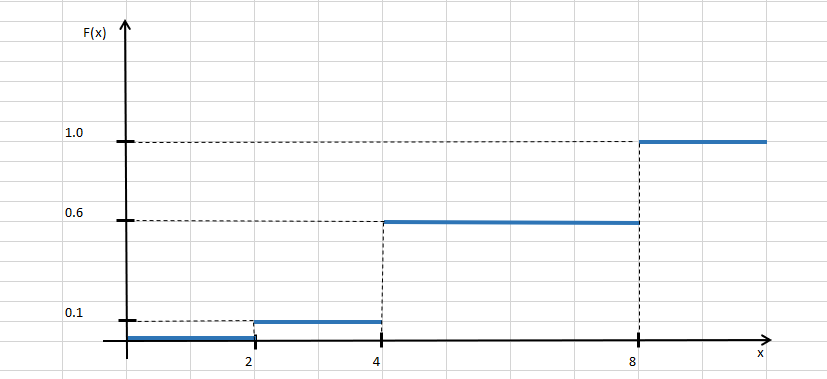
Найти моду, медиану и размах. Вычислим относительные частоты N= 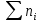 N=10+15+30+33+12=100 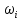 = = 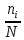 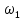 = 10/100=0,1 = 10/100=0,1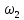 =15/100=0,15 =15/100=0,15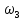 = 30/100=0,3 = 30/100=0,3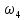 = 33/100=0,33 = 33/100=0,33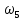 = 12/100=0,12 = 12/100=0,12
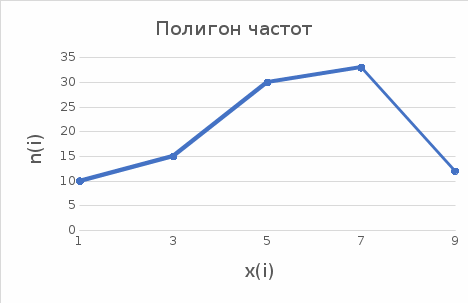 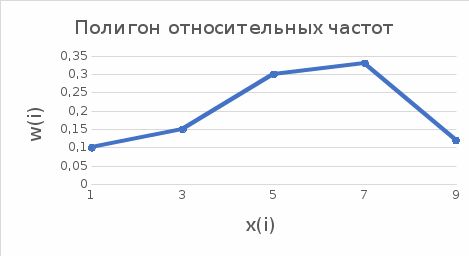 Размах: R= 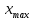 - - 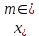 R=9-1=8 Медиана: Me= 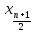 Me= 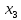 = 5 = 5Мода: Мода — это значение, которое встречается наиболее часто в наборе данных; Некоторые наборы данных не имеют моды, потому что каждое значение встречается только 1 раз, следовательно в нашем случае Мо=0
Вычислим относительные частоты N= 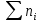 N=9+10+25+6=50 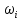 = = 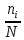 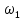 = 9/50=0,18 = 9/50=0,18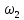 =10/50=0,2 =10/50=0,2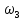 = 25/50=0,5 = 25/50=0,5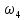 = 6/50=0,12 = 6/50=0,12Построим гистограмму относительных частот 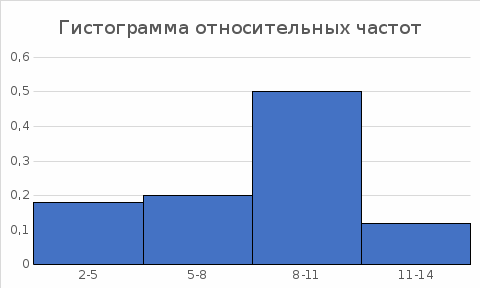 |