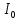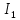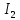Задачи по тоэ. Задачи ТОЭ. Решение Найдем противоположные формы исходных комплексных чисел
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
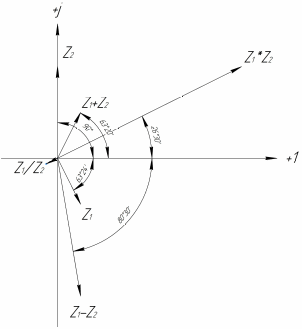
Задача №1 Даны два комплексных числа 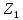 и и 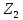 (табл. 1). Необходимо (табл. 1). Необходимовыполнить сложение, вычитание, умножение и деление чисел 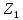 и и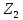 . Исходные и полученные комплексные числа нужно представить . Исходные и полученные комплексные числа нужно представитьв виде векторов на комплексной плоскости.
Решение: Найдем противоположные формы исходных комплексных чисел: 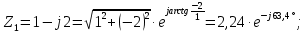 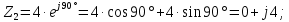 Используя наиболее удобные формы комплексного числа, произведём нужные вычисления: 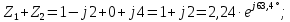 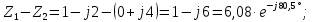 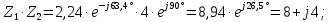 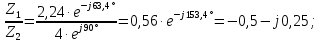
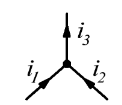
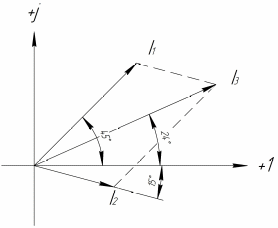
Задача №2 На рисунке 2 показан участок цепи синусоидального тока. Известны законы изменения двух токов (см. табл. 2). Найдите закон изменения неизвестного тока и изобразите все токи на векторной диаграмме.
Решение: Необходимо найти неизвестный ток 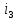 . .Составим уравнение по первому закону Кирхгофа для узла на рис. 2 – алгебраическая сумма сходящихся в узле токов равна нулю: 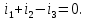 Отсюда находим, что 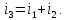 Выполним переход от синусоидально изменяющихся величин к комплексам: 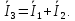 Найдем комплексы тока 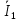 и и 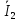 : :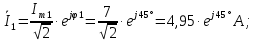 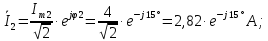 Чтобы сложить комплексы перейдем к алгебраической форме: 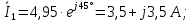 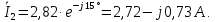 Находим комплекс тока 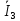 и переводим его в показательную и переводим его в показательнуюформу: 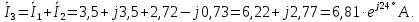 Закон изменения третьего тока: 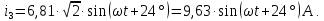
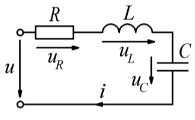
Задача №3 Для схемы на рисунке 3 известно напряжение на одном из элементов и параметры элементов – сопротивление резистора 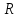 в Ом; индуктивность катушки в Ом; индуктивность катушки 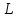 в мГн; емкость конденсатора в мГн; емкость конденсатора 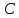 в мкФ. Определить мгновенные значения тока в цепи схемы и напряжения на других элементах, если угловая частота сети в мкФ. Определить мгновенные значения тока в цепи схемы и напряжения на других элементах, если угловая частота сети 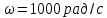 . Построить векторную диаграмму токов и напряжений. . Построить векторную диаграмму токов и напряжений.
Решение: Зная угловую частоту сети 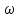 , найдем сопротивления на реактивных элементах: , найдем сопротивления на реактивных элементах: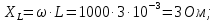 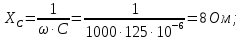 Переведем мгновенное напряжение на резисторе 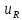 к ксимволической форме: 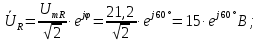 Комплекс тока в цепи можно определить через комплекс напряжения на резисторе и через комплексное сопротивление резистора по закону Ома для резистора. Комплексное сопротивление резистора: 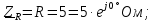 Тогда комплекс тока в цепи: 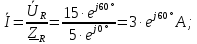 Комплексное сопротивление всего участка равно: 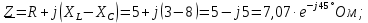 Входное напряжение (напряжение источника) находим по закону Ома для всего участка: 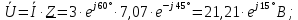 Комплексы напряжения на остальных элементах: 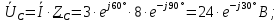 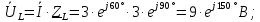 Мгновенные значения всех найденных величин: 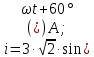 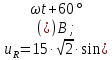 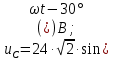 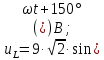
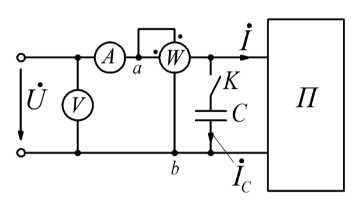
Задача №4 В схеме рис. 4, известны показания измерительных приборов: 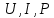 . Также известно показание амперметра после замыкания ключа . Также известно показание амперметра после замыкания ключа 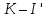 (табл. 4). Определить входное сопротивление двухполюсника. Нарисовать векторную диаграмму токов. (табл. 4). Определить входное сопротивление двухполюсника. Нарисовать векторную диаграмму токов.
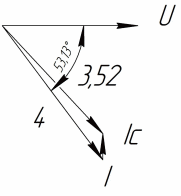
Решение: Определим модуль входного сопротивления: 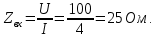 Коэффициент мощности: 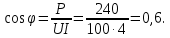 Поскольку замыкание ключа K приводит к уменьшению показаний амперметра, значит характер двухполюсника – активно- индуктивный и угол сдвига фаз 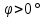 . .Тогда 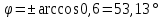 Найдём комплекс входного сопротивления: 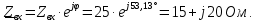 Отсюда активное сопротивление двухполюсника: 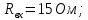 Реактивное сопротивление: 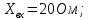
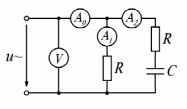
Задача №5 В цепи синусоидального тока (рис. 5), известны показания измерительных приборов. Также известен характер приемников 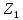 и и 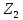 (табл. 5). Необходимо определить (табл. 5). Необходимо определитьактивную мощность, потребляемую цепью.
Решение: 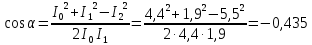 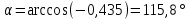 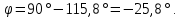 Для определения активной мощности цепи можем воспользоваться следующей формулой: 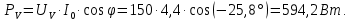 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

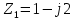
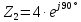
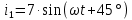
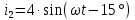
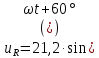
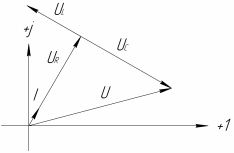
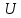 , В
, В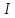 , А
, А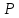 , Вт
, Вт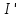 , А
, А