Решение Найдем уравнения изоклин данного дифференциального уравнения, учитывая, что
 Скачать 157.51 Kb. Скачать 157.51 Kb.
|
|
Задача 1. Методом изоклин построить интегральные кривые уравнения 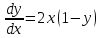 . .Решение: Найдем уравнения изоклин данного дифференциального уравнения, учитывая, что 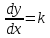 : :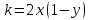 , , 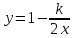 . .При 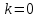 получаем уравнение прямой получаем уравнение прямой 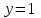 , при , при 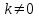 получаем набор гипербол. Сделаем чертеж (изоклины – синие линии, интегральные кривые – красные линии): получаем набор гипербол. Сделаем чертеж (изоклины – синие линии, интегральные кривые – красные линии):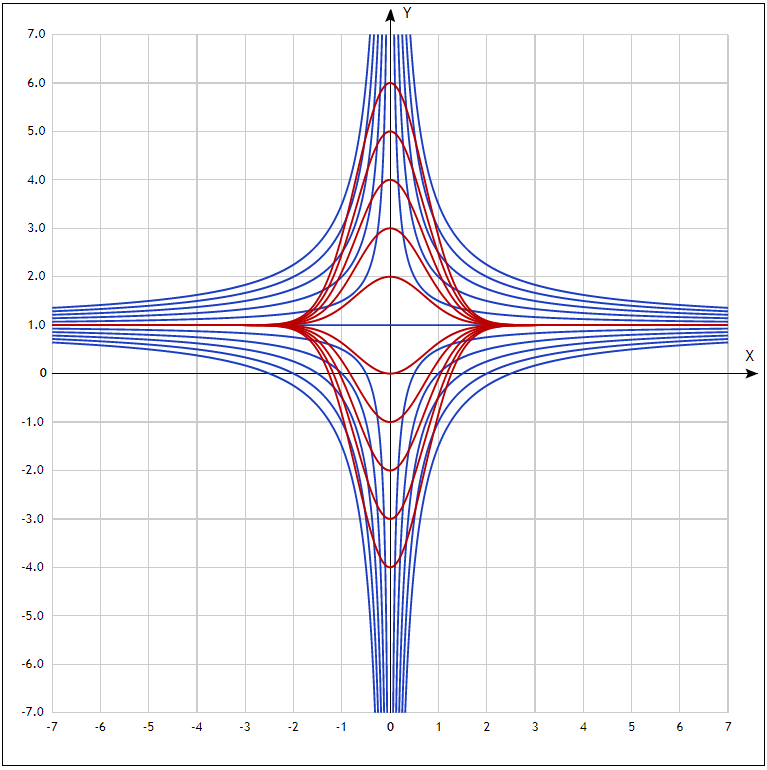 Задача 2. Решить уравнение, допускающее понижение порядка 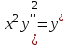 . .Решение: Сделаем замену 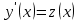 , откуда , откуда 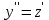 . Тогда получаем уравнение . Тогда получаем уравнение 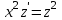 . Разделим переменные: . Разделим переменные: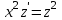 , , 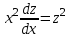 , , 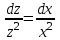 . .Проинтегрируем обе части полученного уравнения: 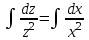 , , 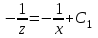 , , 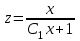 . .С учетом того, что 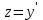 , далее получаем: , далее получаем: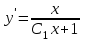 , , 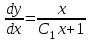 , , 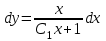 . .Проинтегрируем обе части полученного уравнения: 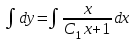 , ,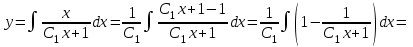 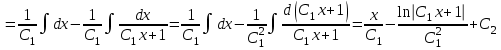 , ,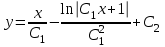 - общее решение данного дифференциального уравнения. - общее решение данного дифференциального уравнения.Задача 3. Решить систему уравнений 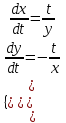 . .Решение: Из первого уравнения получаем, что 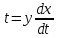 . Подставляя это выражение во второе уравнение, получаем, что . Подставляя это выражение во второе уравнение, получаем, что 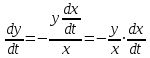 . Разделим переменные и проинтегрируем обе части полученного уравнения: . Разделим переменные и проинтегрируем обе части полученного уравнения: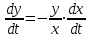 , , 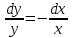 , , 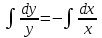 , ,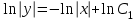 , , 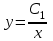 . .Подставляя полученное выражение в первое уравнение, получаем, что 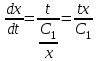 . Разделим переменные и проинтегрируем обе части полученного уравнения: . Разделим переменные и проинтегрируем обе части полученного уравнения: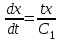 , , 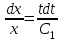 , , 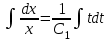 , ,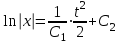 , , 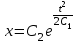 . .Тогда для функции 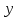 получаем: получаем: 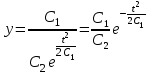 . Следовательно, общее решение данной системы дифференциальных уравнений имеет вид . Следовательно, общее решение данной системы дифференциальных уравнений имеет вид 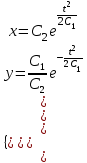 . .Задача 4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение: Данная задача является схемой Бернулли с параметрами 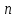 - неизвестное число испытаний и - неизвестное число испытаний и 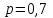 . Наивероятнейшее число появлений события . Наивероятнейшее число появлений события 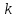 определяется из соотношения определяется из соотношения 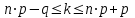 , где , где 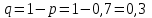 . По условию задачи . По условию задачи 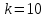 . Тогда получаем: . Тогда получаем: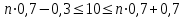 , , 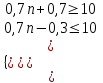 , ,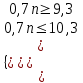 , , 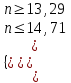 . .Отсюда следует, что искомое число испытаний равно 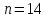 . . |
