Решение Найдемсилу давления масла на поршень гидроцилиндра где глубина погружения центра тяжести площадь поршня
 Скачать 117.07 Kb. Скачать 117.07 Kb.
|
|
Задача 1.1.7 Минеральное масло подается в поршневую полость гидроцилиндра двухстороннего действия с диаметром поршня d = 50 мм. При перемещении поршня на величину lп = 200 мм вентиль 1 закрывают, а к штоку прикладывают усилие F = 3 т (рис. 1). Определить: а) величину изменения положения поршня при приложении нагрузки F; б) то же при условии lп = 1 м; в) то же при условии D = 400 мм; 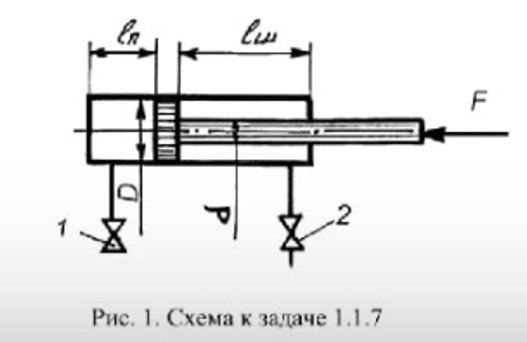 г) то же при условии D = 400 мм и lп = 1 м г) то же при условии D = 400 мм и lп = 1 мДано: d = 50 мм = 0,05 м; D = 400 мм = 0,4 м; lп1 = 200 мм = 0,2 м; lп2 = 1 м; F = 3 т = 29420 Н; ρ = 890 кг/м3. Определить: см. условие задачи Решение:Найдемсилу давления масла на поршень гидроцилиндра: 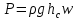 где: 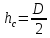 –глубина погружения центра тяжести; –глубина погружения центра тяжести;  –площадь поршня. –площадь поршня.Получаем: 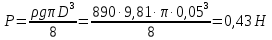 Задача 1.2.15 Цилиндрический сосуд с диаметром D = 1,8 м и высотой H = 3 м соединен с резервуаром трубой А, нижний открытый конец которой погружен под уровень воды в резервуаре. Сосуд установлен на высоте h0 = 2 м над уровнем воды в резервуаре (рис. 16). При закрытом вентиле 1 сосуд через вентиль 2 заполняется водой до высоты h = 2 м. Затем вентиль 2 закрывают, а вентиль 1 открывают. При этом часть воды из сосуда сливается в резервуар. Определить давление воздуха над уровнем воды в сосуде и объем вытекшей воды. 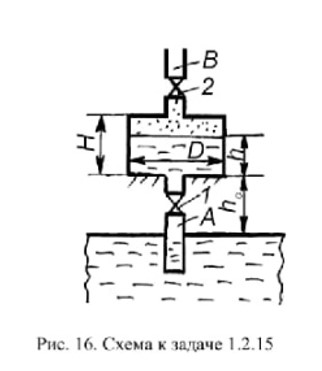 Дано: D = 1,8 м; H = 3 м; h0 = 2 м; Дано: D = 1,8 м; H = 3 м; h0 = 2 м; h = 2 м; pатм = 101325 Па; ρ = 1000 кг/м3. Определить: pв, W Решение: После прекращения вытекания воды установится равновесие – давление на поверхности воды в резервуаре А будет уравновешено суммой давлений воздуха в сосуде и созданного столбом воды: 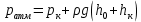 где:  – давление воздуха в сосуде; – давление воздуха в сосуде; 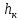 – уровень воды в сосуде. – уровень воды в сосуде.Воспользуемся законом Бойля-Мариотта: 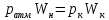 Выразим  : : где: 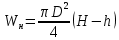 –объем воды в сосуде в начальный момент; –объем воды в сосуде в начальный момент;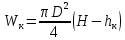 – объем воды в сосуде в конечный момент. – объем воды в сосуде в конечный момент.После всех преобразований получаем:  Подставим: 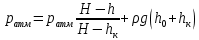 После всех преобразований получаем: 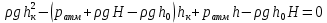 Или: 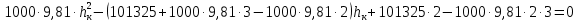 Получаем:  Найдем корни этого уравнения: 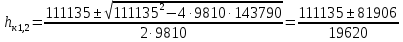 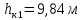 ; ; 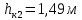 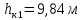 – данное решение не имеет физического смысла, т.к. изначальное значение уровня воды в сосуде: h = 2 м. – данное решение не имеет физического смысла, т.к. изначальное значение уровня воды в сосуде: h = 2 м.Вычислим снижение уровня воды в сосуде:  Следовательно, объем вытекшей воды:  Абсолютное давление в сосуде  найдем: найдем: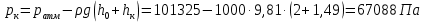 Это давление меньше атмосферного, следовательно, в сосуде вакуум:  Ответ: в сосуде установится вакуум  ; из сосуда вытечет ; из сосуда вытечет 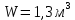 воды. воды. Задача 1.3.23 Резервуар с плоским днищем шириной b и цилиндрическими боковыми стенками радиуса R = 1 м заполнен водой до уровня h = R(рис. 51). Определить силы давления воды на плоское днище и боковые стенки на 1 погонный метр длины резервуара. Как изменяться эти величины, если уровень воды в резервуаре: а) h = R/2; б) h = 3R/2; в) h = 2R? Задача 1.3.23 Резервуар с плоским днищем шириной b и цилиндрическими боковыми стенками радиуса R = 1 м заполнен водой до уровня h = R(рис. 51). Определить силы давления воды на плоское днище и боковые стенки на 1 погонный метр длины резервуара. Как изменяться эти величины, если уровень воды в резервуаре: а) h = R/2; б) h = 3R/2; в) h = 2R?Дано: R = 1 м; h = R = 1 м; b = 1 м; h1 = R/2 = 0,5 м; h2 = 3R/2 = 1,5 м; h3 = 2R= 2 м; ρ = 1000 кг/м3. Определить: P1, P2 Решение: Сила давления воды на 1 м плоского днища равна:  Получаем:   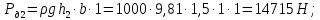  Сила давления на боковые стенки будет состоять из горизонтальной и вертикальной составляющих силы давления: Горизонтальная составляющая силы давления:  где: 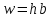 –площадь смоченной поверхности; –площадь смоченной поверхности; 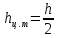 - глубина погружения центра тяжести. - глубина погружения центра тяжести.Получаем: 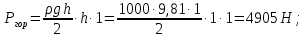  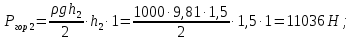  Вертикальная составляющая силы давления: 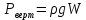 где: W – объем тела давления 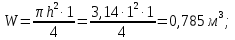 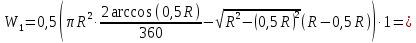 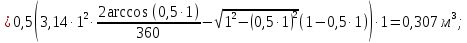      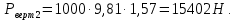 Сила давления на боковую стенку  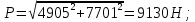 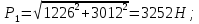 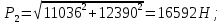 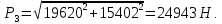 Задача 2.2.5 Водопроводная труба имеет резкое сужение с диаметра d1 = 32 мм до d2 = 16 мм. Расход воды в трубопроводе Q = 1000 л/мин. Определить разность уровней ртути Δh в ртутном дифференциальном манометре, подключенном в месте сужения трубопровода (рис. 78).Как изменятся показания манометра, если объемный расход Q = 2000 л/мин; Q = 500 л/мин? Д  ано: d1 = 32 мм = 0,032 м; ано: d1 = 32 мм = 0,032 м; d2 = 16 мм = 0,016 м; ρв = 1000 кг/м3; Q1 = 1000 л/мин = 0,01667 м3/с; Q2 = 2000 л/мин = 0,03333 м3/с; Q3 = 500 л/мин= 0,008333м3/с; Ρрт = 13540 кг/м3. Определить:Δh Решение. Составим уравнение Д. Бернулли в общем виде для сечений 1-1 (первый участок трубы) и сечения 2-2 (второй участок трубы). Плоскость сравнения - ось трубопровода. Потери напора не учитываем. 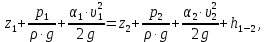 где z1=z2=0; α1=α2=1, тогда уравнение Бернулли запишется в виде 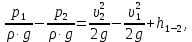 Скорость воды во втором трубопроводе  Составим уравнение неразрывности потока:   Коэффициент местного сопротивления при внезапном сужении трубопровода  где ε - коэффициент сжатия струи  где n - степень сжатия потока   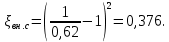 Потери напора 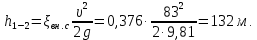 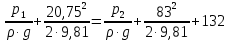 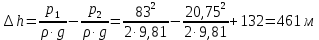 Разность уровней ртути 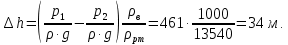 Задача 2.2.28 Минеральное масло поступает в гидравлический цилиндр двухстороннего действия с двухсторонним штоком (диаметр поршня D = 80 мм, диаметр штока d = 30 мм) через дросселирующий распределитель с прямоугольными окнами шириной b= 2 мм и переменной высотой x (изменяется при перемещении золотника) при постоянных давлениях питания pп = 20 МПа и слива pс = 0 МПа (рис. 99). Для полностью открытых окон распределителя (x = 2 мм) определить: а  ) скорость движения поршня гидроцилиндра при нулевой нагрузке (F = 0); ) скорость движения поршня гидроцилиндра при нулевой нагрузке (F = 0);б) нагрузку на штокеF, при которой скорость поршня v = 0. Определить скорость движения поршня при x = 1 мм и F =20 кН. Дано: D = 80 мм = 0,08 м; d = 30 мм = 0,03 м; b= 2 мм = 0,002 м; pп = 20 МПа = 20·106 Па; pс = 0 МПа = 0 Па; x = 2 мм = 0,002 м Определить: см. условие задачи Решение: а) Составим уравнение Д. Бернулли в общем виде для сечений 1-1 (окно распределителя) и сечения 2-2 (в штоковой полости гидроцилиндра). Плоскость сравнения - ось гидроцилиндра. 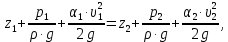 потерями напора и разностью высот пренебрегаем: z1=0; z2=0; α1=α2=1. Тогда уравнение Бернулли примет вид  Составим уравнение неразрывности потока:   Давление в штоковой полости 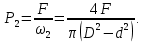 Подставляем эти выражения в уравнение Бернулли и определяем скорость движения жидкости 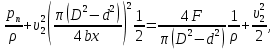 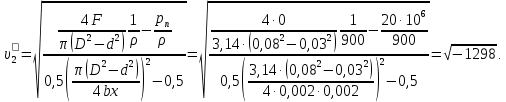 Значение скорости не имеет смысла при F=0. Значит при нулевой нагрузке без учёта потерь напора скорость поршня стремится к бесконечности. б) Нагрузка на поршне при υ2=0:   F=86350 Н. Скорость движения поршня при x = 1 мм и F =20 кН  |
