задачи. Решение задач 8. Решение Найти F
 Скачать 211.58 Kb. Скачать 211.58 Kb.
|
|
| |
| Дано: I1=I2=100 A | Решение:  |
| Найти: F |
Cила взаимодействия двух прямолинейно бесконечно длинных параллельных токов на единицу времени длины
Тогда на провод длинной а, находящийся на расстоянии а от бесконечного провода будет действовать сила
На провод длинной а, находящийся на расстоянии 2а от бесконечного провода будет действовать сила
Из рисунка видно, что суммарная сила равна F=F1-F2. Поэтому

Ответ: 1мН.
418. Протон с энергией 1 МэВ влетел в однородное магнитное поле перпендикулярно линиям индукции (В = 1 Тл). Какова должна быть минимальная протяженность поля в направлении полета протона, чтобы оно изменило направление движения протона на противоположное?
| Дано: W=1МэВ=1,6·10-13 Дж В=1Тл m=1,67·10-27 Кг q= 1,6·10-19 Кл | Решение:  Протон будет вращаться в магнитном поле по окружности. Минимальная протяженность поля l в направлении движения протона будет равна радиусу окружности R. (R=lmin) Cила Лоренца, действующая на частицу: Fл=q·v·B По ІІ закону Ньютона F=m·a, где ускорение а при движении по окружности: а=v2/R q·v·B= mv2/R R=m·v/(q·B) Скорость протона найдем из формулы энергии: W=mv2/2  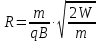 = = = =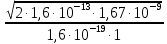 =0,1445 м=14,45 см =0,1445 м=14,45 см |
| Найти: lmin |
Ответ: 14,45 см.
428. Обмотка тороида, имеющего стальной сердечник с узким вакуумным зазором, имеет 1000 витков. По обмотке течет ток в 1 А. При каком вакуумном зазоре индукция магнитного поля в нем будет равна 0,5 Тл (см. рис. 16)? (Длина тороида по средней линии равна 1 м.)

| Дано: N=1000 I=1 A B=0,5 Тл l=1 м | Решение: На основании закона полного тока: I·N=H·l+Ho·lo Где Н и Но – напряженность поля в сердечнике и в зазоре соответственно.  |
| Найти: lo |
По графику зависимости В от Н, определяем, что для стали при B=0,5 Тл напряженность Н=100 А/м.
Для воздуха
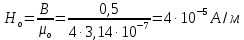


Ответ: 2,25 мм.
435*. Рамка из провода сопротивлением 0,01 Ом равномерно вращается в однородном магнитном поле с индукцией 0,05 Тл. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Площадь рамки 100 см2. Определить, какое количество электричества протечет через рамку за время поворота ее на угол 30° в трех случаях: 1) от 0 до 30°, 2) от 30 до 60°, 3) от 60 до 90°.
| Дано: R=0,01 Ом В=0,05 Тл S=100 см2=100·10-4 м2. α=30° от 0 до 30°, от 30 до 60°, от 60 до 90. | Решение:  По закону электромагнитной индукции:  где Ф-магнитный поток: Ф=B·S·cosα, S- площадь контура, α - угол между вектором магнитной индукции и нормалью к рамке ε=dФ/dt = B·S·d(cos(α))/dt I =ε/R = B·S/R ·d(cos(α))/dt По закону Ома для замкнутой цепи: ∆Q = ∫ I·dt =∫ BS/R · d(cos(α))/dt·dt = B·S/R ·∫d(cos(α)) = B·S/R ·∆(cos(α)) ∆Q = B·S/R · ∆(cos(α)) 1) от 0 до 30°: |∆Q| = B·S/R · |cos(30)-cos(0)| = 0,05 · 100·10-4· (1 -  ) Кл/0,01 = 6,70·10-3 Кл 6,7 мКл ) Кл/0,01 = 6,70·10-3 Кл 6,7 мКл2) от 30 до 60°: |∆Q| = B·S/R · |cos(60)-cos(30)| = 0,05 · 100·10-4· (  -1/2) Кл /0,01 =0,0183 Кл 18,3 мКл. -1/2) Кл /0,01 =0,0183 Кл 18,3 мКл.3 мКл 3) от 60 до 90° |∆Q| = B·S/R ·|cos(90)-cos(60)| = 0,05 · 100·10-4· (1-1/2) Кл/0,01 =0,025 Кл 25 мКл |
| Найти: ΔQ |
Ответ: 1) 6,7 мКл, 2) 18,3 мКл 3) 25 мКл.
442. Катушка, намотанная на цилиндрический каркас, имеет N = 750 витков и индуктивность L1 = 25 мГн. Чтобы увеличить индуктивность до L2 = 36 мм, обмотку с катушки сняли и заменили обмоткой из более тонкой 106 проволоки с таким расчетом, чтобы длина катушки осталась прежней. Сколько витков оказалось в катушке после перемотки?
| Дано: N1=750 L1=25 мГн L2=36 мГн | Решение: Известно, что индуктивность L=μo·μ·n2·V, Где V=S·1 – объем соленоида, μ – магнитная проницаемость сердечника (в нашем случае μ=1), n – числа витков на единицу длины соленоида. Величина n=N/1, где N – число витков, так как намотка однослойная. Поэтому 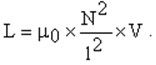 Тогда отношение:  Откуда искомое число витков  |
| Найти: N2 |
Ответ: 900.
602. Определить температуру и энергетическую светимость абсолютно черного тела, если максимум энергии излучения приходится на длину волны 400 нм.
| Дано: λ=400 нм=400·10-9 м | Решение: Интенсивность излучения где Р – мощность, т.е энергия излучения за 1с, S – поверхность, сквозь которую проходит энергия. Эта энергия, излучаемая за 1с с единицы поверхности абсолютно черного тела, определяется формулой Стефана-Больцмана: где σ=5,67·10-8 Вт/м2К4 Закона смещения Вина: где С1=2,9·10-3 м·К |
| Найти: Т RT |
Поэтому
 .
.
RT=5,67·10-8 Вт/м2К4·(7250 К)4=15,64·10-7 Вт/м2.
Ответ: 15,64·10-7 Вт/м2.
609. Определить кинетическую энергию электронов, вылетевших из цинка, при освещении его лучами с длиной волны 220 нм.
| Дано: λ=220 нм=220·10-9 м | Решение: Работа выхода электрона из цинка Aв=6,4⋅10−19Дж Отсюда: 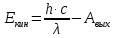  =2,6· =2,6· |
| Найти: Екин |
Ответ: 2,6·

616. Определить длину волны, которую испускает однозарядный ион гелия Не+ при переходе со второго энергетического уровня на первый.
| Дано: Не+, 2→1 | Решение: По формуле Бальмера частота света, испускаемого при переходе с уровня n2 на уровень n1: 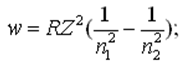 где R=2,07·1016 с-1 – постоянная Ридберга, Z - порядковый номера атома. Тогда длина волны λ:  Для Не+ Z=2. Подставляем соответствующие числа в формулу: 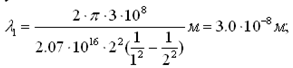 |
| Найти: λ |
Ответ: 3,0·10-8 м.
