высшая математика задание 1. Решение. Найти область определения, точки разрыва
 Скачать 128.5 Kb.
|
|
Задание. Для функции  :1. Найти область определения, точки разрыва. 2. Исследовать функцию на чётность, периодичность. 3. Исследовать поведение функции на концах области определения. Указать асимптоты. 4. Найти промежутки монотонности. Точки экстремума. 5. Найти промежутки выпуклости. Точки перегиба. 6. Найти площадь фигуры, ограниченной графиком функции и прямыми  ,  ,  .Решение. 1. Найти область определения, точки разрыва. Функция не имеет точек, в которых он не определена, то есть точек разрыва нет и область определения функции лежит а интервале  .2. Исследовать функцию на чётность, периодичность. Проверим функцию на чётность:  =  .Функция не чётная и не нечётная. Функция не содержит тригонометрических выражений, значит, она не периодическая. 3. Исследовать поведение функции на концах области определения. Указать асимптоты.  ; .Уравнение асимптот:  .Здесь    = .Прямая - горизонтальная асимптота функции при  .4. Найти промежутки монотонности. Точки экстремума. Находим производную функции:  =  .При     .Находим знак производной на интервалах:   - функц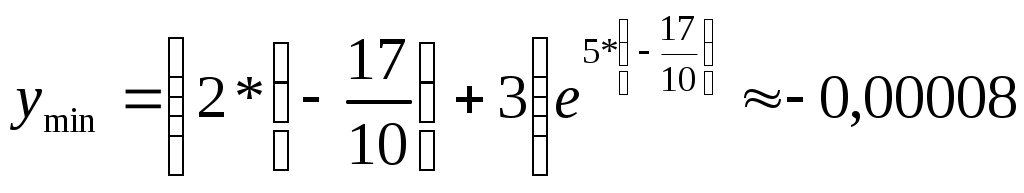ия убывает;  - функция возрастает.Точка - точка минимума. .5. Найти промежутки выпуклости. Точки перегиба. Находим вторую производную функции:  =  .При    .Находим знак производной на интервалах:   - графи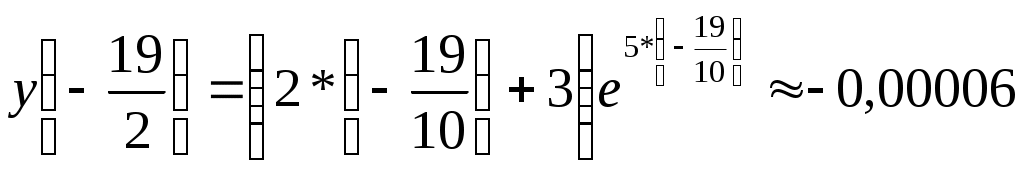к выпуклый;  - график вогнутый.Точка - точка перегиба. .6. Найти площадь фигуры, ограниченной графиком функции и прямыми , , .Площадь трапеции находим через определённый интеграл: 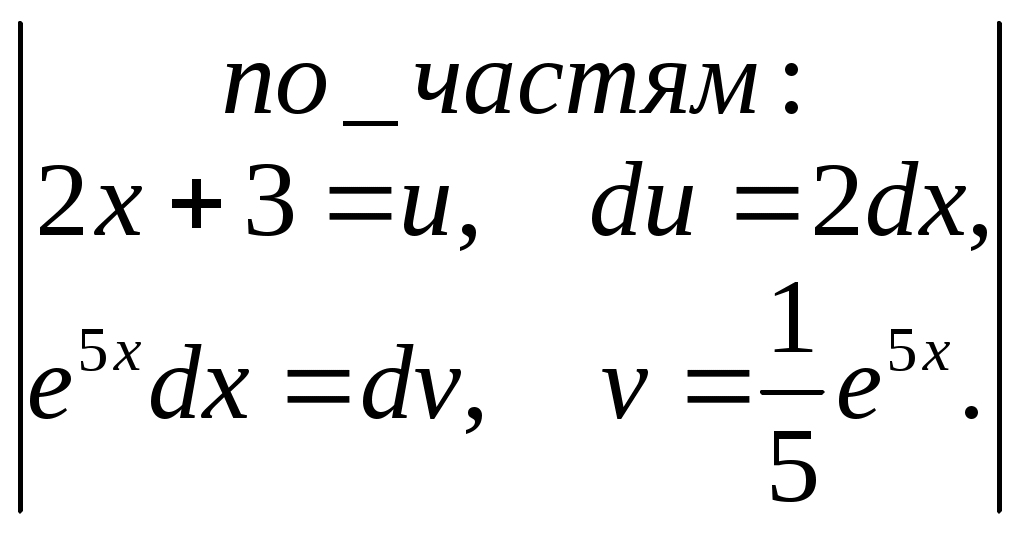 =  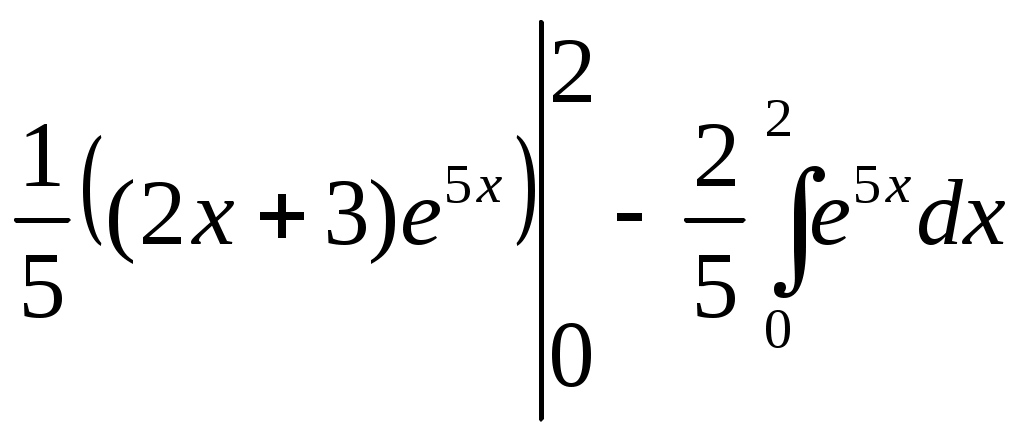=  = 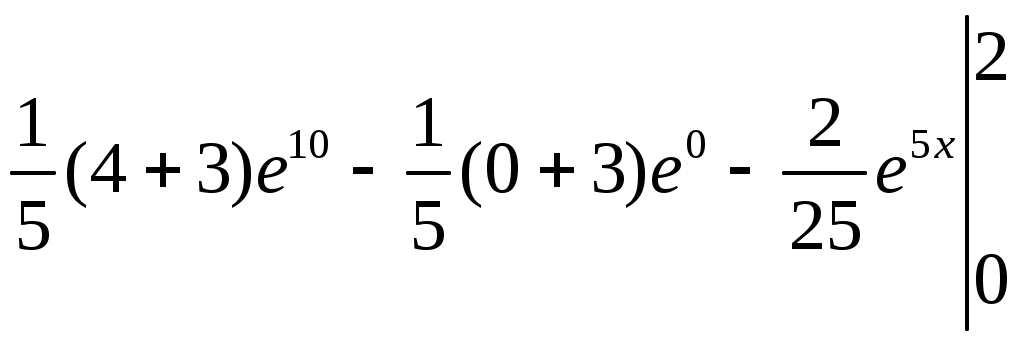 = =  =  =  .Результаты исследования:
|
