ЗАДАНИЕ_3_. Решение нам нужно найти число различных комбинаций из 3 элементов (3 книги), выбранных из множества, состоящего из 43 элементов (43 книги по научной фантастике).
 Скачать 27.84 Kb.
|
Практическое задание 3Задание №1 В домашней библиотеке у Василия Петровича собрано 43 книги по научной фантастике. Он хочет взять с собой в отпуск 3 книги для чтения. Сколькими способами Василий Петрович может это сделать? В кино отправились 9 друзей. Сколькими разными способами они могут встать в очередь на кассе? Таблица, размером 99*99, раскрашена в шахматном порядке в белый и черный цвета. Верхняя левая клетка – черная. Сколькими способами можно указать в таблице два квадрата – белый и черный? Задание №2 При игре в кости бросаются два игральных кубика и подсчитывается сумма выпавших очков. Найти вероятность событий: А – сумма равна 6; В – сумма больше 8. Из имеющихся 16 телевизоров 11 готовы к продаже, а 5 требуют дополнительной регулировки. Найти вероятности событий: А – из случайно отобранных 4 телевизоров все хорошие, В – два хорошие и два нет, С – один хороший и три нет, D – хороших нет. Туристическая группа состоит из 10 юношей и 6 девушек. По жребию (случайным образом) выбирают 3 дежурных. Найти вероятность того, что будут выбраны 1 девушка и 2 юноши. Задание №1 В домашней библиотеке у Василия Петровича собрано 43 книги по научной фантастике. Он хочет взять с собой в отпуск 3 книги для чтения. Сколькими способами Василий Петрович может это сделать? 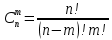 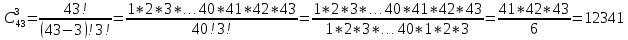 Ответ: 12341 В кино отправились 9 друзей. Сколькими разными способами они могут встать в очередь на кассе? Решение: в этой задаче у нас будут комбинации, состоящие из одних и тех же элементов, отличаются эти комбинации только порядком расположения элементов. Участвуют все элементы множества (все 9 друзей встают в очередь к кассе), значит речь идет о перестановках из 9 элементов. Воспользуемся формулой: Pn = n! 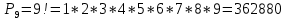 Ответ:362880 Таблица, размером 99*99, раскрашена в шахматном порядке в белый и черный цвета. Верхняя левая клетка – черная. Сколькими способами можно указать в таблице два квадрата – белый и черный? Решение: так как размеры таблицы 99*99, то число элементов в столбцах нечетное. По условию, в первом столбце первая клетка – черная, значит черных клеток на 1 больше (клетки чередуются, всего 99, значит белых 49, а черных 50). В каждом следующем столбце с нечетным номером ситуация такая же, белых клеток там 49, черных -50, а столбцов 50 (1-й, 3-й, 5-й, … ,99-й). В столбцах с четными номерами ситуация такая: первая клетка – белая, значит, белых – 50, а черных – 49. Столбцов же всего 49 с четными номерами. Подсчитаем, сколько всего белых клеток и сколько черных. 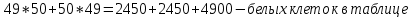 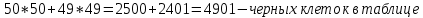 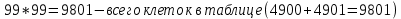 Выбираем 1 белую клетку 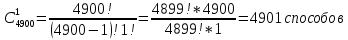 Выбираем 1 черную клетку 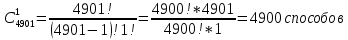 Следовательно, указать в таблице два квадрата – белый и черный, можно 4900*4901=24014900 способами Ответ: 24014900 способов Задание №2 При игре в кости бросаются два игральных кубика и подсчитывается сумма выпавших очков. Найти вероятность событий: А – сумма равна 6; В – сумма больше 8. Решение: так как бросают 2 игральных кубика, то число возможных вариантов равно 6*6 = 36. Составим таблицу возможных вариантов выпадения очков (верхняя строка – очки на гранях первого кубика, левый столбик – очки на гранях второго кубика). Число вариантов, что при бросании двух кубиков сумма выпавших очков будет равна 6, равно 5, значит, вероятность события А – «сумма равна 6» будет равна 5:36 =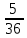 
1+5 = 6, 2 + 4 = 6, 3 + 3 = 6, 4 +2 = 6, 5 + 1 = 6 - 5 благоприятных исходов. Число вариантов, что при бросании двух кубиков сумма выпавших очков больше 8, равна 10, значит, вероятность события В – «сумма больше 8» равна 10:36 =  =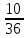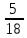 
3+6=9, 4+5=9, 4+6=10, 5+4=9, 5+5=10, 5+6=11, 6+3=9, 6 + 4 = 10, 6 + 5 = 11, 6 + 6 = 12 - 10 благоприятных исходов Ответ: 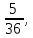 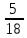Из имеющихся 16 телевизоров 11 готовы к продаже, а 5 требуют дополнительной регулировки. Найти вероятности событий: А – из случайно отобранных 4 телевизоров все хорошие, В – два хорошие и два нет, С – один хороший и три нет, D – хороших нет. Решение: так всего телевизоров 16, выбрать нужно 4, то число возможных вариантов найдем по формуле 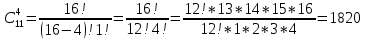 Выбираем только хорошие. Их всего 11, нам нужно 4. Считаем: 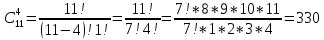 Вероятность события А – из случайно отобранных 4 телевизоров все хорошие будет равна 330:1820 = 33:182 = 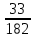  Если хороших (готовых к продаже) телевизоров 11, то 16 – 11 = 5 телевизоров требуют дополнительной доработки.Выбираем 2 хороших и 2 нет. 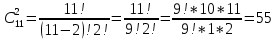 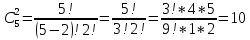 55*10 = 550 Вероятность события В – из случайно отобранных телевизоров 2 хороших, а 2 нет, равна 550:1820 = 55 :182 = 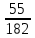 Выбираем 1 хороший и 3 нет. 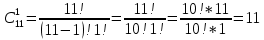 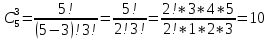 11*10 = 110 Вероятность события С – из случайно отобранных телевизоров 1 хороший, а три нет, равна 110:1820 = 11 :182 = 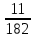 Событие D – хороших нет означает, что нужно выбрать 4 телевизора из 5 «плохих» (требующих доработки). 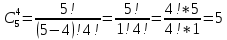 Вероятность события D – из случайно отобранных 4 телевизоров нет хороших, равна 5:1820 = 1:364 = 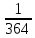 Ответ: 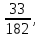 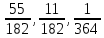 Туристическая группа состоит из 10 юношей и 6 девушек. По жребию (случайным образом) выбирают 3 дежурных. Найти вероятность того, что будут выбраны 1 девушка и 2 юноши. Решение: всего туристов 10 + 6 = 16 человек. Выбираем случайным образом 3 человек из 16. 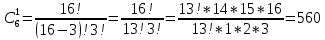 Выбираем 1 девушку из 6 и 2 юношей из 10. 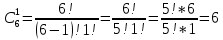 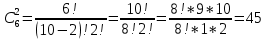 45*6=270 Вероятность того, что будут выбраны 1 девушка и 2 юноши, равна 270 : 560 = 27:56= 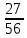 Ответ: 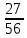|