мАТЕМАТИКА. Матеметика. Кафедра математических и естественнонаучных дисциплин
 Скачать 61.5 Kb.
|
 Кафедра математических и естественно-научных дисциплин Рейтинговая работа расчетно-аналитическое задание по дисциплине Теория вероятностей и математическая статистика Задание/вариант № 5 Тема* ______________________________________________________________ Выполнена обучающимся группы УЗДтс 28.2/Б1-21 Шнайдмиллер Анастасия Олеговна (фамилия, имя, отчество) Преподаватель __________________________________ (фамилия, имя, отчество) Москва – 2022 г. СОДЕРЖАНИЕЗадача 1 3 Задача 2 4 Задача 1Завод изготовил две партии телевизоров. Первая партия телевизоров в два раза больше второй. Надежность телевизоров первой партии – 0,9, второй партии – 0,8. Определить вероятность того, что наугад купленный телевизор будет надежным. Пусть x телевизоров изготовлено второй партией, тогда первой партией изготовлено 2x телевизоров. x+2x =1 3x=1 x=1/3 Р (D1) – телевизор изготовленный первой партией – 2/3 Р (D2) − телевизор изготовленный второй партией – 1/3 V – купленный телевизор будет надежным. Вероятность этого события: РD1(V)= 089 PD2(V)=0,8 По формуле: P(V)= 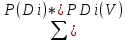 = 2/3*0,9+1/3*0,8= 13/15 ≈0,8667Ответ: 0,8667 Задача 2В парке отдыха организована беспроигрышная лотерея. Имеется 1000 выигрышей, из них 400 – по 100 руб.; 300 – по 200 руб.; 200 – по 1000 руб. и 100 – по 2000 руб. Какой средний размер выигрыша для посетителя парка, купившего один билет? Случайная величина A − размер выигрыша, может принимать четыре значения: 100, 200, 1000, 2000 р. Первому результату благоприятствуют 400 случаев из 1000, второму - 300, третьему – 200 и четвертому 100. Поэтому их вероятности таковы: P1=400/1000=0,4 P2=300/1000=0,3 Р3=200/1000=0,2 Р4=100/1000=0,1 Закон распределения
Математическое ожидание: М (А)= 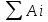 PiМ (А)=100*0,4+200*0,3+1000*0,2+2000*0,1=500 Ответ: средний размер выигрыша для посетителя парка, купившего один билет, составит 500 рублей. |