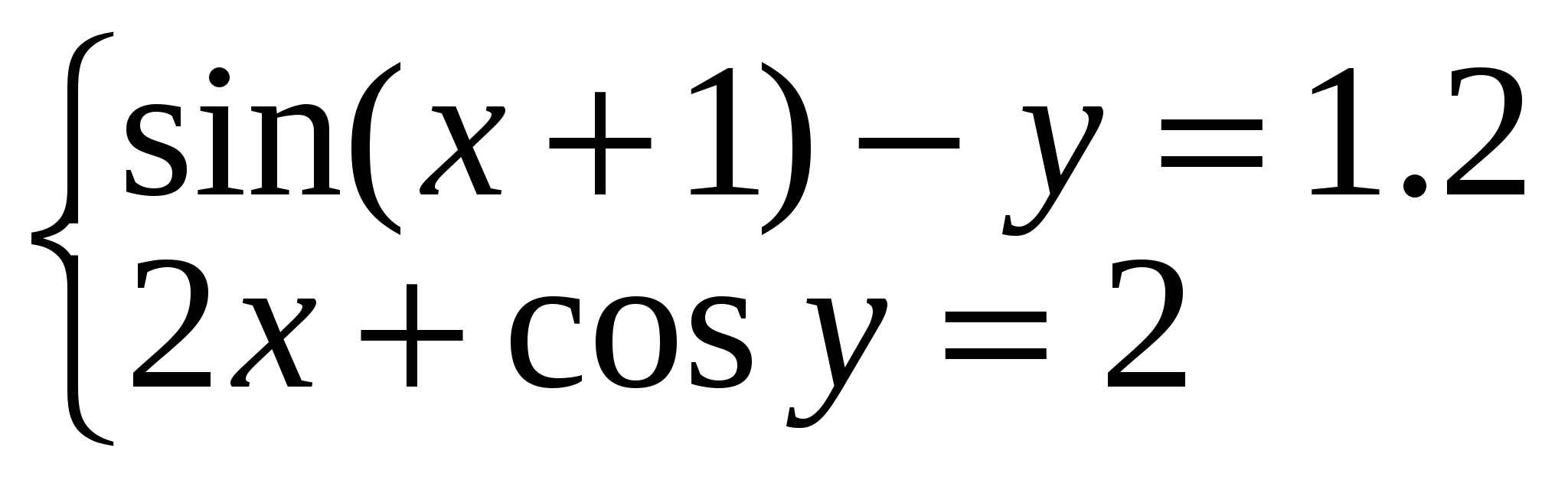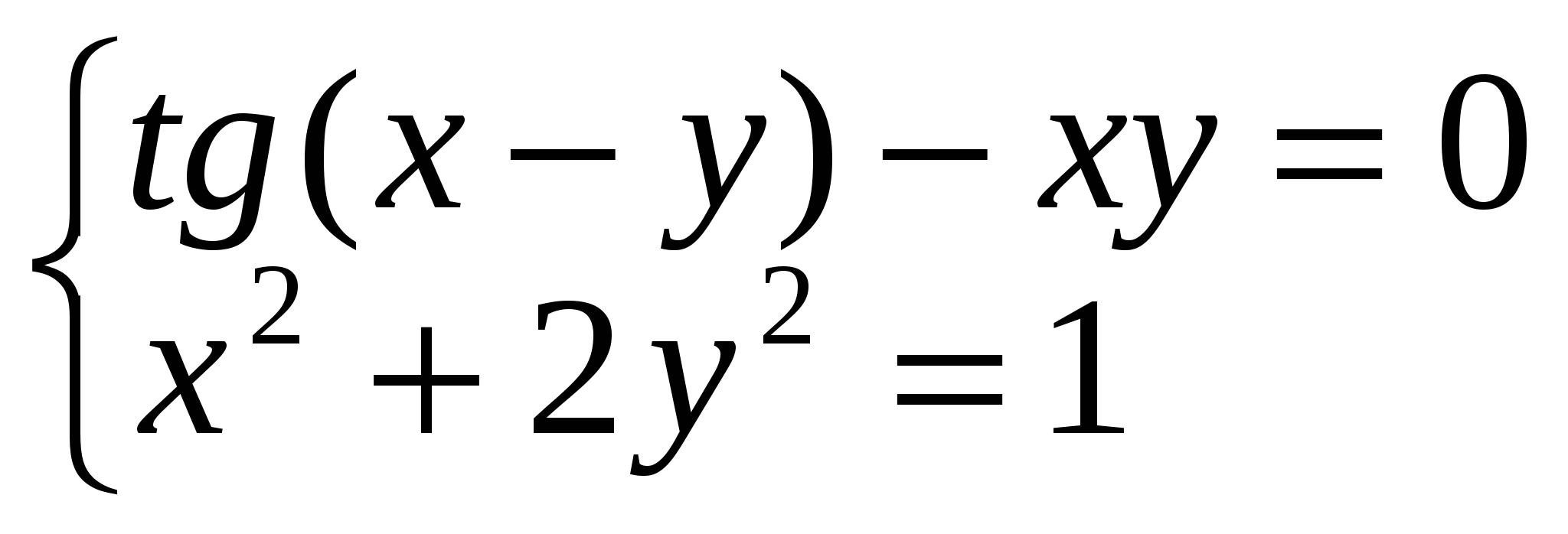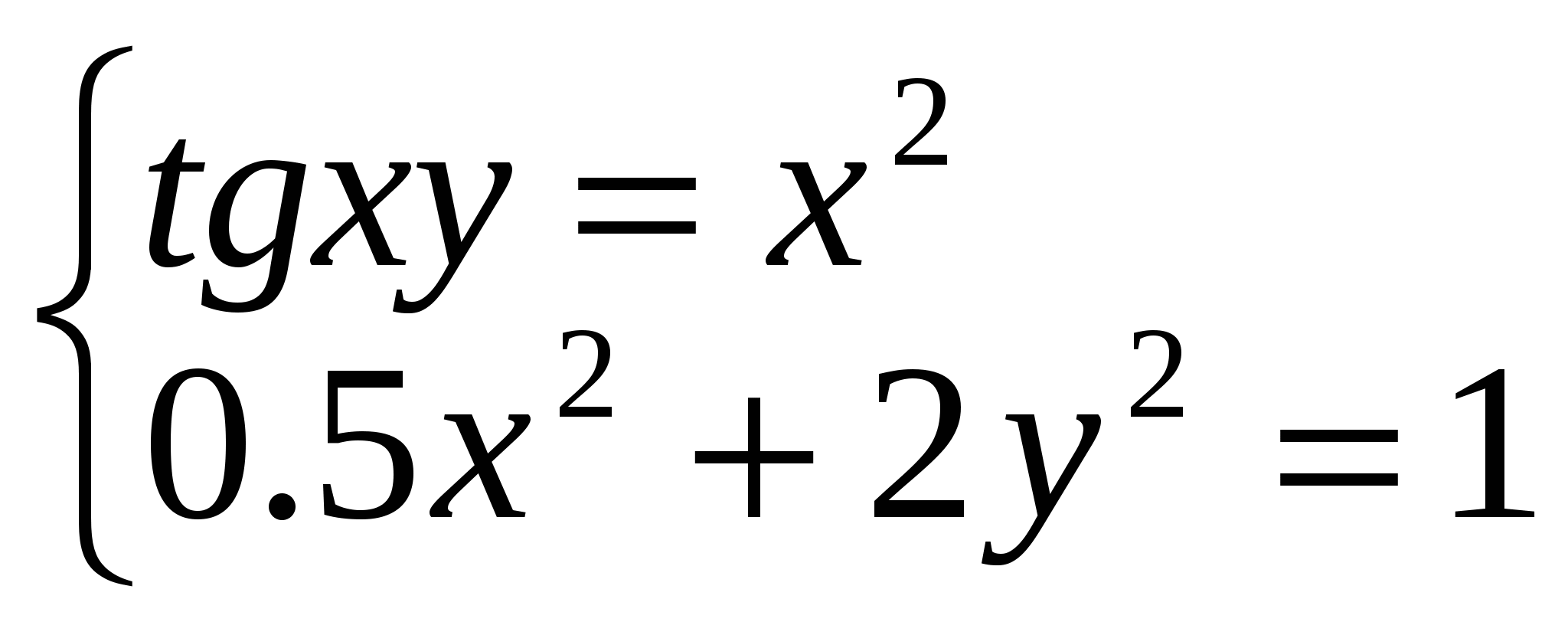решение уравнений в excel. Решение нелинейных уравнений и систем
 Скачать 488.5 Kb. Скачать 488.5 Kb.
|
|
Решение нелинейных уравнений и систем» Цель работы: Изучение возможностей пакета Ms Excel 2007 при решении нелинейных уравнений и систем. Приобретение навыков решения нелинейных уравнений и систем средствами пакета. Задание1. Найти корни полинома x3 - 0,01x2 - 0,7044x + 0,139104 = 0. Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x, при котором функция обращается в ноль. Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0,2. Результаты вычислений приведены на ри., где в ячейку В2 была введена формула: = A2^3 - 0,01*A2^2 - 0,7044*A2 + 0,139104. На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеется не более трех вещественных корней, то графическое решение поставленной задачи найдено. Иначе говоря, была проведена локализация корней, т.е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8]. 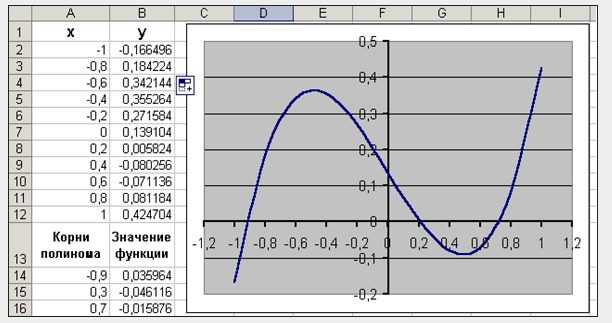 Теперь можно найти корни полинома методом последовательных приближений с помощью команды Данные→Работа с данными→Анализ «Что-Если» →Подбор параметра. После ввода начальных приближений и значений функции можно обратиться к команде Данные→Работа с данными→Анализ «Что-Если» →Подбор параметра и заполнить диалоговое окно следующим образом. 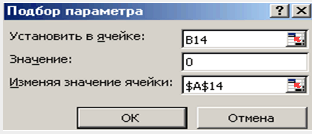 В поле Установить в ячейке дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения (уравнение должно быть записано так, чтобы его правая часть не содержала переменную). В поле Значение вводим правую часть уравнения, а в поле Изменяя значения ячейки дается ссылка на ячейку, отведенную под переменную. Заметим, что вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке. После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра с сообщением об успешном завершении поиска решения, приближенное значение корня будет помещено в ячейку А14. 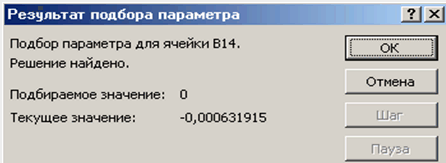 Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и А16.  Задание 2. Решить уравнение ex- (2x - 1)2 = 0. Проведем локализацию корней нелинейного уравнения. Для этого представим его в виде f(x) = g(x) , т.е. ex = (2x - 1)2 или f(x) = ex, g(x) = (2x - 1)2, и решим графически. Графическим решением уравнения f(x) = g(x) будет точка пересечения линий f(x) и g(x). Построим графики f(x) и g(x). Для этого в диапазон А3:А18 введем значения аргумента. В ячейку В3 введем формулу для вычисления значений функции f(x): = EXP(A3), а в С3 для вычисления g(x): = (2*A3-1)^2. Результаты вычислений и построение графиков f(x) и g(x):  На графике видно, что линии f(x) и g(x) пересекаются дважды, т.е. данное уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно: 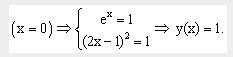 Для второго можно определить интервал изоляции корня: 1,5 < x < 2. Теперь можно найти корень уравнения на отрезке [1.5,2] методом последовательных приближений. Введём начальное приближение в ячейку Н17 = 1,5, и само уравнение, со ссылкой на начальное приближение, в ячейку I17 = EXP(H17) - (2*H17-1)^2. Далее воспользуемся командой Данные→Работа с данными→Анализ «Что-Если» →Подбор параметра. и заполним диалоговое окно Подбор параметра. 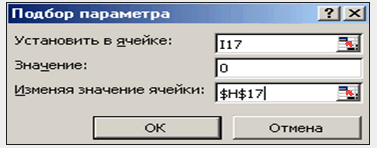 Результат поиска решения будет выведен в ячейку Н17.  Задание 3. Решить систему уравнений: 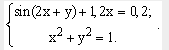 Прежде чем воспользоваться описанными выше методами решения систем уравнений, найдем графическое решение этой системы. Отметим, что оба уравнения системы заданы неявно и для построения графиков, функций соответствующих этим уравнениям, необходимо разрешить заданные уравнения относительно переменной y. Для первого уравнения системы имеем: Выясним ОДЗ полученной функции: 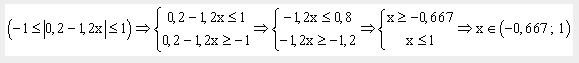 Второе уравнение данной системы описывает окружность. Фрагмент рабочего листа MS Excel с формулами, которые необходимо ввести в ячейки для построения линий, описанных уравнениями системы. Точки пересечения линий изображенных являются графическим решением системы нелинейных уравнений.  Не трудно заметить, что заданная система имеет два решения. Поэтому процедуру поиска решений системы необходимо выполнить дважды, предварительно определив интервал изоляции корней по осям Оx и Oy . В нашем случае первый корень лежит в интервалах (-0.5;0)x и (0.5;1)y, а второй - (0;0.5)x и (-0.5;-1)y. Далее поступим следующим образом. Введем начальные значения переменных x и y, формулы отображающие уравнения системы и функцию цели. 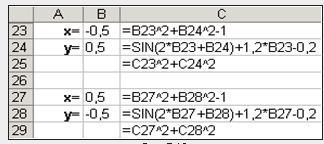 Теперь дважды воспользуемся командой Данные→Анализ→Поиск решений, заполняя появляющиеся диалоговые окна. 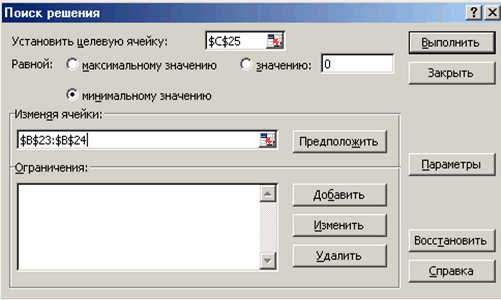  Сравнив полученное решение системы с графическим, убеждаемся, что система решена верно.  Задания для самостоятельного решения Задание 1. Найти корни полинома Задание 2. Найдите решение нелинейного уравнения. Задание 3. Найдите решение системы нелинейных уравнений. |